- 1使用VS Code开发STM32_vs code stm32
- 2大数据Hive篇--UDF函数
- 3贪心算法 定义+特性+原理+公式+Python示例代码(带详细注释)_贪心算法代码
- 4从本地仓库提交到gitee报错:DeployKey does not support push code
- 5Infrared and visible image fusion using Latent Low-Rank Representation使用潜在低秩表示的红外与可见光融合
- 6[Leetcode] 802. Find Eventual Safe States 解题报告_802. find eventual safe states解题报告 python
- 7LLM大模型的演进与发展_llm进化路线与现状
- 8深入了解 Python 中的变量_python中是没有变量的
- 9Python+Fiddler5带你爬取6000+高清王者荣耀cosplay图_王者荣耀抓包人脸软件
- 10TCP的滑动窗口和拥塞控制_tcp窗口
2024年亚太中文赛B题第一版论文 首发+问题一代码免费分享_洪水灾害的数据分析与预测模型假设有哪些
赞
踩
亚太(中文赛)分享资料(问题一代码+论文+思路)链接(已更新完毕):
链接:https://pan.baidu.com/s/14REVRHSvZUTOrY9zDlOvwA
提取码:sxjm
洪水灾害的数据分析与预测
摘要
洪水是由暴雨、急剧融冰化雪、风暴潮等自然因素引起的江河湖泊水量迅速增加或水位迅猛上涨的一种自然现象,也是自然灾害之一。本文将基于题目给出的数据,实现对洪水灾害的预测。
对于题目提供的数据,首先需要进行数据清洗,即利用KS检验+Q-Q图判定分布方式,对于正态分布的数据使用3西格玛原则判定异常值,对于非正态分布的数据使用箱型图判定异常值。对于异常值进行剔除处理,因为剔除而导致的缺失值、数据本身的缺失值使用克里金插值进行填充。利用数据清洗后的数据集,绘制可视化结果进行题目给出数据的描述。
对于问题一,数据分析和可视化。首先利用数据预处理后的结果,使用皮尔逊相关系数计算各指标与洪水发生概率之间的相关性。使用Seaborn绘制相关性矩阵热力图,直观展示各指标之间的相关性。分析哪些指标与洪水发生概率的相关性较强,哪些指标相关性较弱。为了进一步分析每个指标与洪水发生概率的关系,使用线性回归或其他回归方法拟合数据。根据相关性分析和可视化结果,讨论各指标对洪水发生的潜在影响机制。
针对问题二,将洪水发生的概率聚类成不同类别。使用KMeans算法将数据聚类成3类(低风险、中风险、高风险),并将结果添加为“风险类别”列。使用随机森林分类器来计算每个特征的重要性,并绘制特征重要性的柱状图。这个步骤有助于识别对风险类别划分最重要的特征。基于特征重要性选择最重要的5个特征来建立随机森林分类器模型。评估模型性能,并输出分类报告。逐个移除重要特征,并重新训练模型,以观察模型性能的变化,从而进行灵敏度分析。
针对问题三,预测模型的建立与求解。我们首先标准化特征数据,以使得每个特征在同一尺度上。将数据集分割为训练集和测试集,其中30%的数据作为测试集,70%的数据作为训练集。定义四种回归模型:线性回归、决策树回归、随机森林回归和梯度提升回归。对每个模型分别进行训练,并在测试集上进行预测。计算每个模型的均方误差和决定系数,以评估模型性能。以误差最小为目标函数,权重系数和为1约束,构建优化模型,利用粒子群智能算法进行求解。绘制加权预测结果与真实值的散点图,直观展示加权模型的预测性能。利用随机森林分类器,选取特征重要性最高的前5个特征,对选取的5个重要特征进行标准化。重复上述步骤,进行限制指标数量的预测。
针对问题四,利用问题三得到的预测模型对test文件进行预测。最终得到结果R-squared为0.86,Mean Squared Error为0.0003,具有良好的结果精度。利用预测的结果,使用 Kolmogorov-Smirnov 检验和 Anderson-Darling 检验,并绘制直方图、折线图以及 QQ 图,得出所有检验的p值都为0,表明洪水概率数据显著偏离正态分布。这些结果表明数据不服从正态分布。
关键词:洪水灾害,数据分析,预测模型,数据清洗,相关性分析,灵敏度分析
对数据进行箱型图检验,使用MATLAB中boxplot 函数来生成箱型图并标识异常值。箱型图是一种用于显示一组数据分布的图表,其中“异常值”通常被定义为小于 Q1 1.5IQR 或大于 Q3 + 1.5IQR 的值(其中 Q1 是第一四分位数,Q3 是第三四分位数,IQR 是四分位间距)。
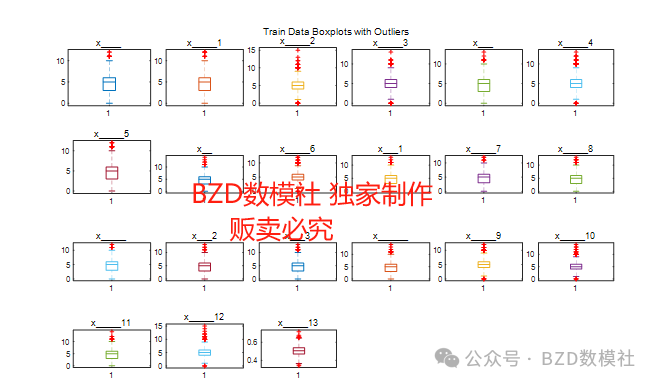
图1:异常值判定图
对于判定出的结果,我们进行人为判定,最终得出对于“地形排水”数据,存在三个数值为18的数据,该数据相对于全部数据集为异常数据,我们需要剔除处理。对于剔除后的数据,我们利用克里金插值进行填充。
对其中空缺值使用克里金插值进行补充。克里金插值的基础是统计假设,即空间上接近的事物更有可能表现出相似的特性。它使用了已知位置的数据来预测未知位置的值,基于空间数据的协方差或半方差结构来进行。
l半方差函数(Semivariogram):
半方差函数是描述空间数据相关性的关键工具。它表示为距离的函数,描述了随着样本间距离的增加,样本值的差异(半方差)如何变化。
半方差函数的形状和范围为克里金插值提供了参数,如块金效应(nugget)、基台值(sill)和变程(range)。
块金效应表示在非常小的距离内的变异,可以解释为测量误差或小尺度变异。
基台值是半方差函数的平稳值,表明样本间的最大差异。
变程是达到基台值所需的距离,表明数据的空间自相关的范围。
l权重的确定:
克里金插值计算未知点的值时,会根据已知点到未知点的距离及其方向,利用半方差函数来确定权重。
这些权重用于加权平均已知数据点的值,以估计未知位置的值。
l优化和求解:
克里金方法通过解线性方程组来找到权重,这些线性方程由已知数据点的半方差值定义。
目标是最小化预测误差的方差,确保估计是最优的、无偏的。
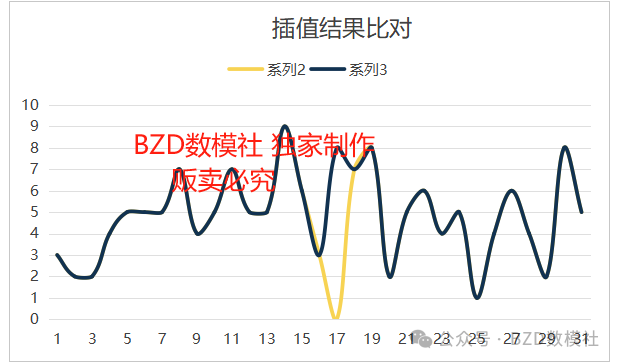
5.1.2 数据可视化
我们对数据预处理后的数据进行可视化处理,得到结果如下所示

图1:不同指标在不同洪水发生概率区间内的分布情况
这张图展示了不同指标在不同洪水发生概率区间内的分布情况,通过箱线图的形式进行可视化。每个子图对应一个指标,并展示了该指标在不同洪水概率区间内的分布。首先,X轴代表洪水概率区间,这些区间是通过分位数划分的,具体包括:[0.348, 0.465)、[0.465, 0.503)、[0.503, 0.534)、[0.534, 0.61]。Y轴则代表每个指标的取值范围。这种可视化方式可以直观地比较不同洪水概率区间内各指标的分布和中位数的变化。人口得分、气候变化和侵蚀等指标在不同洪水概率区间内的分布相对均匀,但存在一些差异。例如,在较高洪水概率区间内,人口得分的中位数略高,这可能表明高人口密度区域更容易发生洪水。
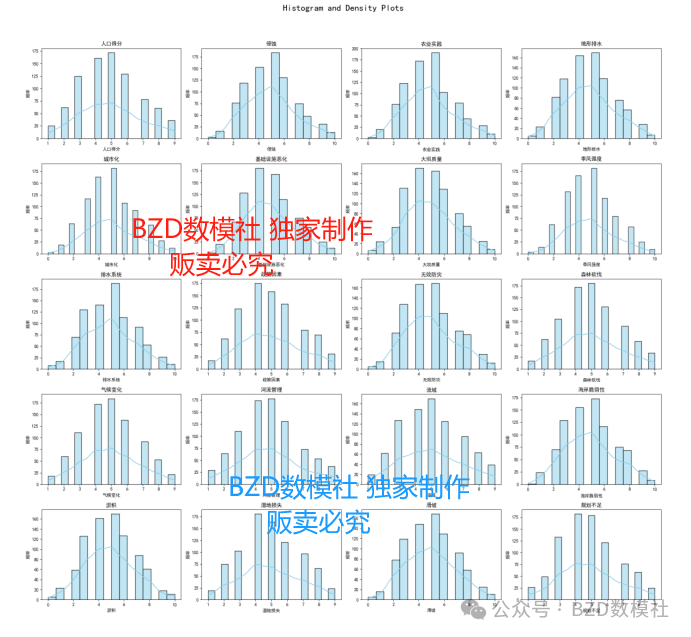
图1:各指标直方图和密度图
这张图展示了各个指标的分布特征,通过直方图和密度图的组合形式来进行可视化分析。每个子图代表一个指标,展示了该指标在整个数据集中的分布情况。通过这些直方图和密度图,我们可以观察到以下几点:
首先,许多指标的分布接近正态分布,如侵蚀、农业实践、大坝质量、河流管理、气候变化和政策因素等。这些指标的直方图呈现出钟形曲线,且核密度估计曲线与直方图较为吻合,表明这些指标在数据集中大部分取值集中在均值附近,呈现对称分布。
其次,一些指标的分布较为偏态,如人口得分、森林砍伐、城市化、排水系统和湿地损失等。这些指标的直方图显示出较为明显的偏态分布,核密度估计曲线的峰值也偏向一侧,表明这些指标在数据集中存在某种程度的偏斜,即大部分取值集中在某个方向。此外,图中还显示了一些指标的多峰分布,如基础设施恶化和规划不足,这些指标的直方图和核密度估计曲线都展示出多个峰值,表明这些指标的数据在不同区间内有较高的频数,可能存在多个不同的集中趋势。
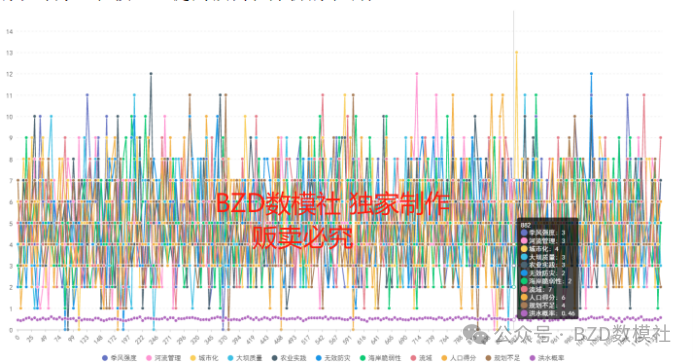
图1:数据预处理数据可视化
这张图展示了多个不同指标在数据预处理后的分布情况,具体描述如下:
图中每条线代表一个不同的指标,不同颜色表示不同的指标。图例中列出了所有20个指标及其对应的颜色,包括:季风强度、地形排水、河流管理、森林砍伐、城市化、气候变化、大坝质量、淤积、农业实践、侵蚀、无效防灾、排水系统、海岸脆弱性、滑坡、流域、基础设施恶化、人口得分、湿地损失、规划不足、政策因素。大部分指标在整个样本范围内呈现出显著的波动。一些指标的波动幅度较大,表现出显著的上升和下降趋势;例如,某些指标在特定数据点上的数值会突然上升或下降。图中的数据点密集且变化频繁,
最终得到部分结果如下所示,
| 洪水概率 | |||
| id | 0.021234811 | 无效防灾 | 0.204940273 |
| 季风强度 | 0.110153744 | 排水系统 | 0.212027962 |
| 地形排水 | 0.161737003 | 海岸脆弱性 | 0.161821842 |
| 河流管理 | 0.226009257 | 滑坡 | 0.179157251 |
| 森林砍伐 | 0.198266884 | 流域 | 0.13881526 |
| 城市化 | 0.171529893 | 基础设施恶化 | 0.165902118 |
| 气候变化 | 0.20020163 | 人口得分 | 0.169339199 |
| 大坝质量 | 0.191884027 | 湿地损失 | 0.238314011 |
| 淤积 | 0.175772405 | 规划不足 | 0.208217902 |
| 农业实践 | 0.132247353 | 政策因素 | 0.216727459 |
| 侵蚀 | 0.163207715 | 洪水概率 | 1 |
为了进一步直观地展示结果,我们使用Seaborn绘制相关性矩阵热力图,直观展示各指标之间的相关性。
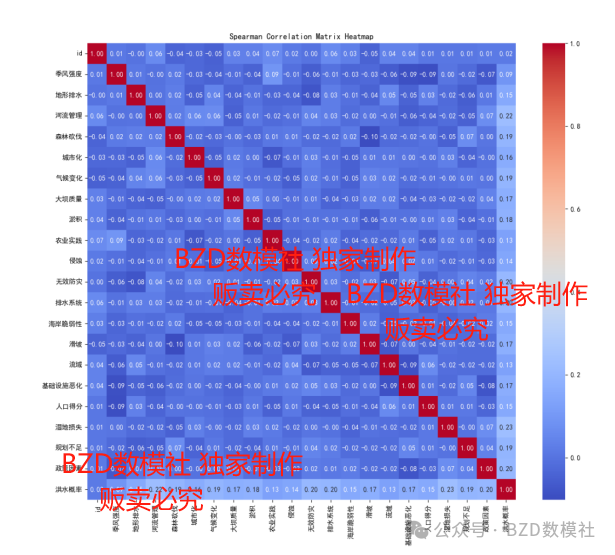
图1:矩阵热力图
这张Spearman相关性矩阵热力图直观地展示了洪水灾害各指标之间的相关性情况,以及具体的数值表明了每个指标与洪水概率的相关性强度。通过这张热力图和给出的具体相关性数值,可以进一步理解哪些因素对洪水概率有重要影响。
首先,从热力图的颜色梯度来看,红色表示强正相关,蓝色表示强负相关,白色表示弱相关或无相关。在相关性矩阵中,我们可以观察到“洪水概率”这一列的颜色变化情况,以了解各个指标与洪水概率的相关性。
具体数据表明,森林砍伐、河流管理、无效防灾、排水系统和湿地损失等指标与洪水概率有较强的正相关性,相关系数分别为0.198、0.226、0.205、0.212和0.238。这意味着这些因素在某种程度上会增加洪水发生的可能性。例如,森林砍伐导致的水土流失和河流管理不当可能使洪水更容易发生,而无效防灾措施和排水系统不足则直接影响洪水的防控效果。


