热门标签
热门文章
- 1你觉得做为一名开发负责人需要具备哪些特质--chatgpt回答_开发项目负责人 需要具备
- 2Django进阶:DRF(Django REST framework)_django drf
- 3Kafka 最佳实践:构建高性能、可靠的数据管道_kafka消费模式最佳实践
- 4python转换成c语言_将Python转换成C语言,然后用Cython编译成exe
- 5记 搭建pycharm远程连接spark的艰难过程_importerror: no module named findspark
- 6从零开始研发GPS接收机连载——3、用HackRF软件无线电平台作为GPS模拟器_gps sdr sim
- 7utf8mb4_0900_ai_ci_utf8mb40900aici
- 8Java项目:客户关系管理系统(java+SpringBoot+layui+html+maven+mysql)_java 管理系统角色划分
- 9Hadoop集群环境配置及安装配置(详细过程包含安装包)_hadoop安装与配置_hadoop 配置
- 10深度学习笔记(九):神经网络剪枝(Neural Network Pruning)详细介绍
当前位置: article > 正文
十大经典排序算法(Java实现)_java基础排序算法
作者:正经夜光杯 | 2024-06-26 10:47:53
赞
踩
java基础排序算法
排序算法的重要性不言而喻,为了加深对这十种算法的理解,固写此文。
首先排序算法可以分为内部排序算法和外部排序算法:在内存中进行的称为内部排序算法,也就是这里所说的这十种算法;相应的,当数据量很大时无法全部拷贝到内存需要使用外存,称为外部排序算法。接下来我们可用如下表来简单概括这十种算法:
| 十大经典排序算法 | 平均时间复杂度 | 最好时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|---|---|
| 冒泡排序 | O \Omicron O(n2) | O \Omicron O(n) | O \Omicron O(n2) | O \Omicron O(1) | In-place | 稳定 |
| 选择排序 | O \Omicron O(n2) | O \Omicron O(n2) | O \Omicron O(n2) | O \Omicron O(1) | In-place | 不稳定 |
| 插入排序 | O \Omicron O(n2) | O \Omicron O(n) | O \Omicron O(n2) | O \Omicron O(1) | In-place | 稳定 |
| 希尔排序 | O \Omicron O(n1.3) | O \Omicron O(n) | O \Omicron O(n2) | O \Omicron O(1) | In-place | 不稳定 |
| 归并排序 | O \Omicron O(n log \log log2n) | O \Omicron O(n log \log log2n) | O \Omicron O(n log \log log2n) | O \Omicron O(n) | Out-place | 稳定 |
| 快速排序 | O \Omicron O(n log \log log2n) | O \Omicron O(n log \log log2n) | O \Omicron O(n2) | O \Omicron O( log \log log2n) | In-place | 不稳定 |
| 堆排序 | O \Omicron O(n log \log log2n) | O \Omicron O(n log \log log2n) | O \Omicron O(n log \log log2n) | O \Omicron O(1) | In-place | 不稳定 |
| 计数排序 | O \Omicron O(n+k) | O \Omicron O(n+k) | O \Omicron O(n+k) | O \Omicron O(k) | Out-place | 稳定 |
| 桶排序 | O \Omicron O(n+k) | O \Omicron O(n+k) | O \Omicron O(n2) | O \Omicron O(n+k) | Out-place | 稳定 |
| 基数排序 | O \Omicron O(n*k) | O \Omicron O(n*k) | O \Omicron O(n*k) | O \Omicron O(n+k) | Out-place | 稳定 |
| 表中数据说明: |
- 稳定:如果A原本在B前面,而A=B,排序之后A仍然在B的前面;
- 不稳定:如果A原本在B的前面,而A=B,排序之后A可能会出现在B的后面;
- 时间复杂度: 描述一个算法执行所耗费的时间;
- 空间复杂度:描述一个算法执行所需内存的大小;
- n:数据规模;
- k:“桶”的个数;
- In-place:占用常数内存,不占用额外内存;
- Out-place:占用额外内存。
该十种排序算法可分为如下所示的两大类
- 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(n log \log logn),因此也称为非线性时间比较类排序。
- 非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。

1、冒泡排序(Bubble Sort)
算法步驟
- 比较相邻的元素,如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的比价,从开始第一对到结尾的最后一对,这样在最后的元素就是最大的数;
- 针对所有的元素重复以上的步骤,除了数组最后已经排好序的数组;
- 重复步骤1~3,直到排序完成。

代码实现
public class BubbleSort { public static void bubbleSort(int[] arr) { int len = arr.length; for (int i = 0; i < len - 1; i++) { boolean flag = true; for (int j = 0; j < len - i - 1; j++) { if (arr[j] > arr[j + 1]) { int tmp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = tmp; flag = false; } } if (flag) { break; } } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
2、选择排序(Selection Sort)
算法步驟
- 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置;
- 再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾;
- 重复第2步,直到所有元素均排序完毕。

代码实现
public class SelectionSort { public static void selectionSort(int[] arr) { int len = arr.length; for (int i = 0; i < len - 1; i++) { int minVal = i; for (int j = i + 1; j < len; j++) { if (arr[minVal] > arr[j]) { minVal = j; } } if (minVal != i) { int tmp = arr[i]; arr[i] = arr[minVal]; arr[minVal] = tmp; } } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
3、插入排序(Insertion Sort)
算法步驟
- 首先从第一个元素开始,该元素被认为是有序的;
- 取出下一个元素,在已经排序的元素序列中从后往前进行扫描;
- 如果该已排好序的元素大于新元素,则将该元素移到下一位置;
- 重复步骤3一直往前进行扫描比较,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤2~5。

代码实现
public class InsertionSort {
public static void insertionSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int val = arr[i], j = i;
while (j > 0 && val < arr[j - 1]) {
arr[j] = arr[j - 1];
j--;
}
arr[j] = val;
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
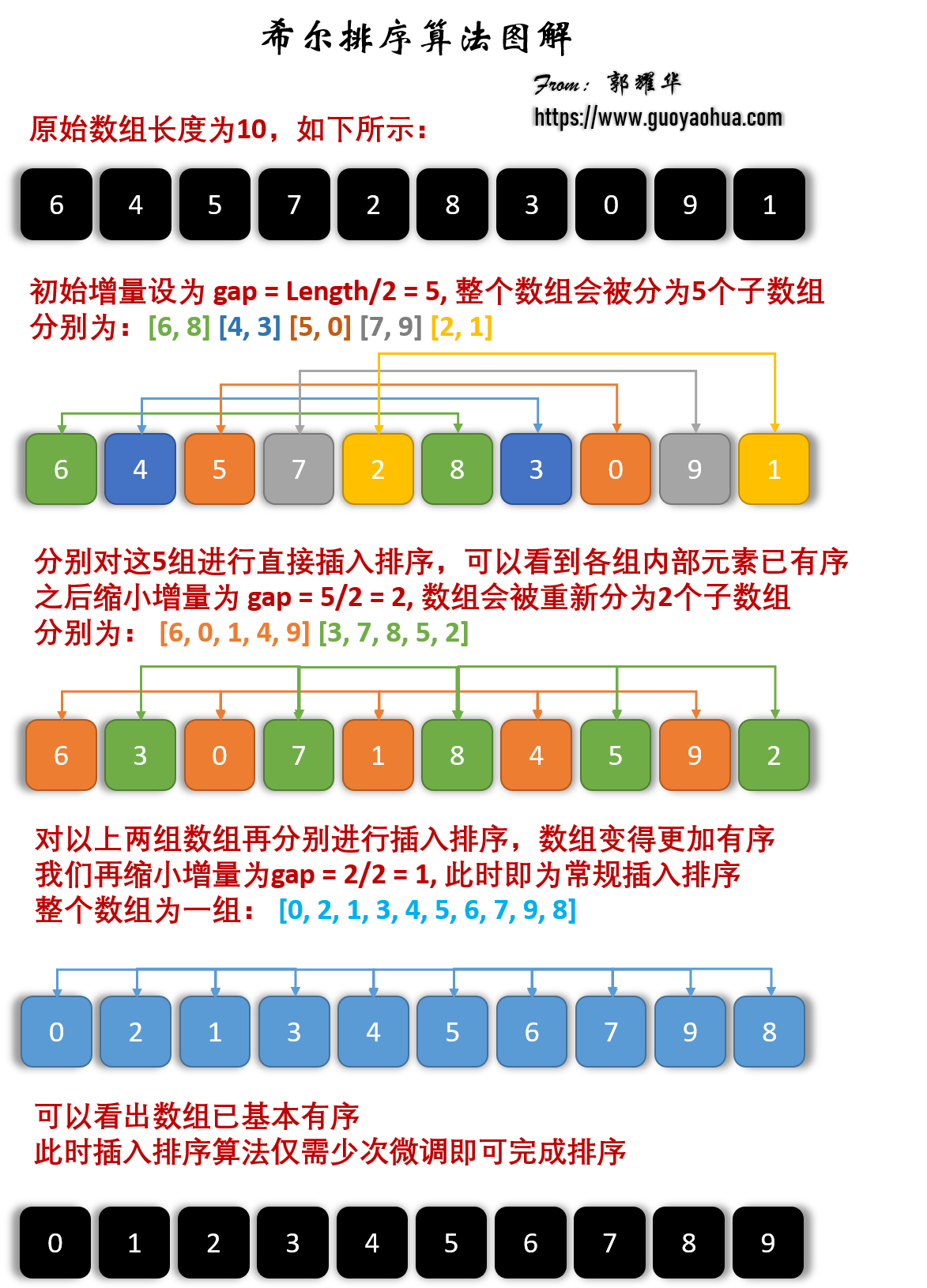
4、希尔排序(Shell Sort)
算法步驟
- 选择一个增量序列{t1, t2, …, tk};
- 按增量序列个数k,对序列进行k趟排序;
- 每趟排序,根据对应的增量t,将待排序列分割成若干长度为m的子序列,分别对各子表进行直接插入排序。仅增量因子为1时,整个序列作为一个表来处理,表长度即为整个序列的长度。
其中,增量gap=length/2,缩小增量继续以gap = gap/2的方式,这种增量选择我们可以用一个序列来表示,{n/2, (n/2)/2, …, 1},称为增量序列。一般的增量序列都选择以上说明的这个,但不一定是最优的。
代码实现
public class ShellSort { public static void shellSort(int[] arr) { int len = arr.length, tmp, j; for (int gap = len / 2; gap >= 1; gap = gap / 2) { for (int i = gap; i < len; i++) { tmp = arr[i]; j = i - gap; while (j >= 0 && arr[j] > tmp) { arr[j + gap] = arr[j]; j -= gap; } arr[j + gap] = tmp; } } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
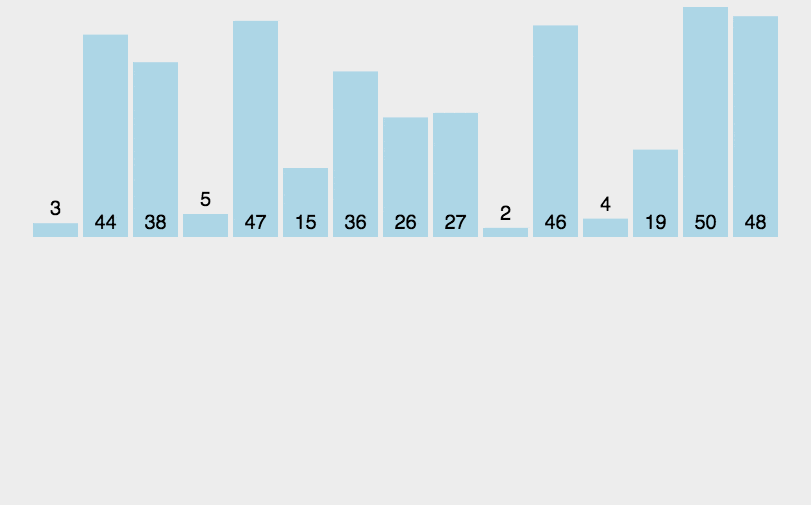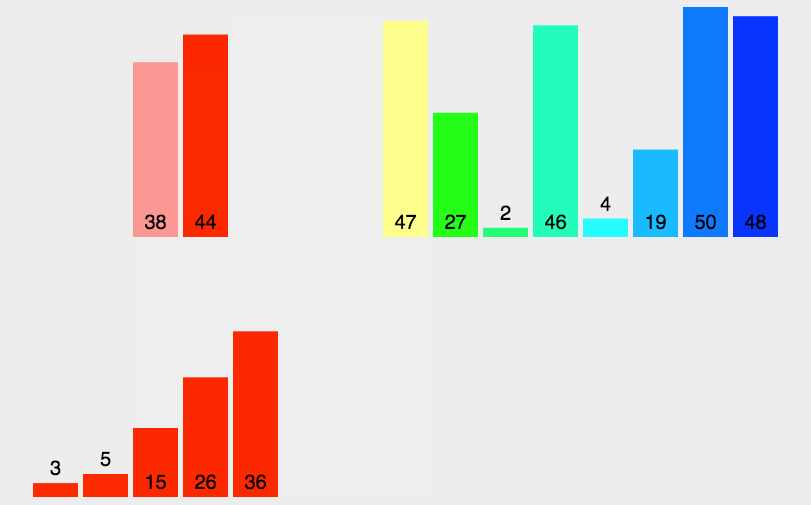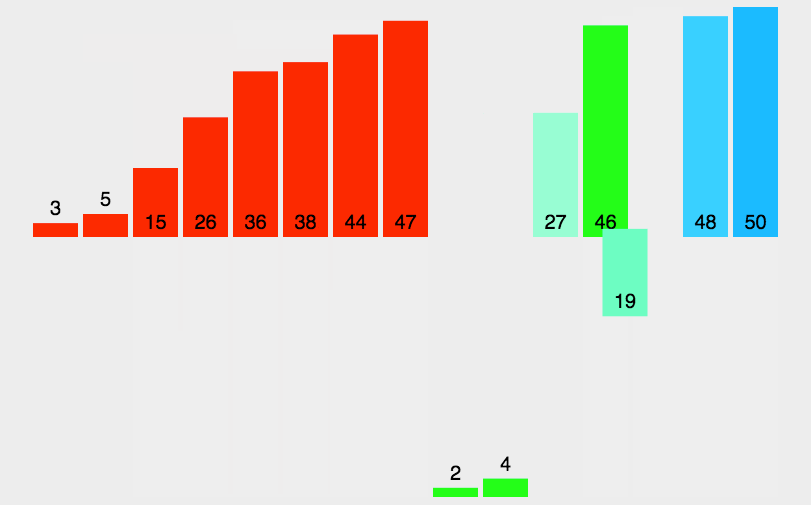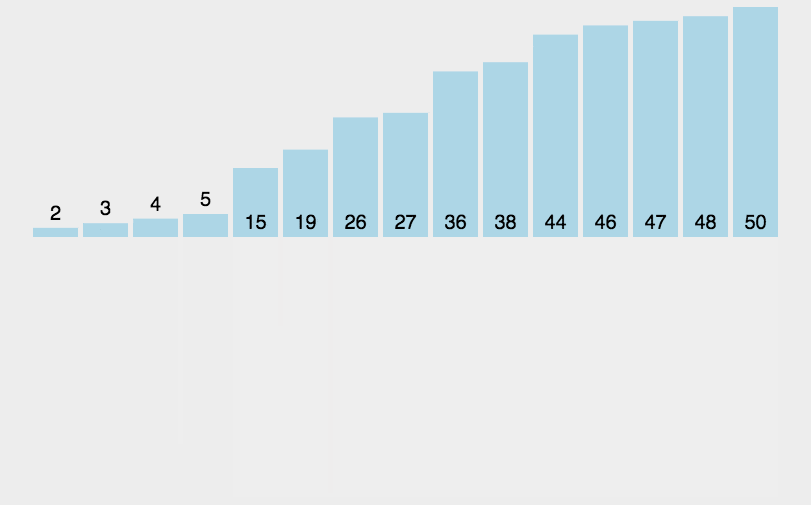
5、归并排序(Merge Sort)
算法步驟
- 如果待排序列只有一个元素,则直接返回,否则将长度为n的待排序列分成两个长度为n/2的子序列,递归进行调用进行分割知道每个子序列中只有一个元素;
- 此时的每个子序列被认为是有序的,然后递归调用的返回子序列进行两两合并;
- 合并过程中完成排序操作,具体操作为设定两个指针,分别指向两个已经排序子序列的起始位置;
- 比较两个指针所指向的元素,选择相对小的元素放入到合并返回的数组,并移动指针到下一位置;
- 重复步骤3~4直到某一指针达到序列尾;
- 将另一序列剩下的所有元素直接复制到合并序列尾,最终得到的新序列就是有序序列。
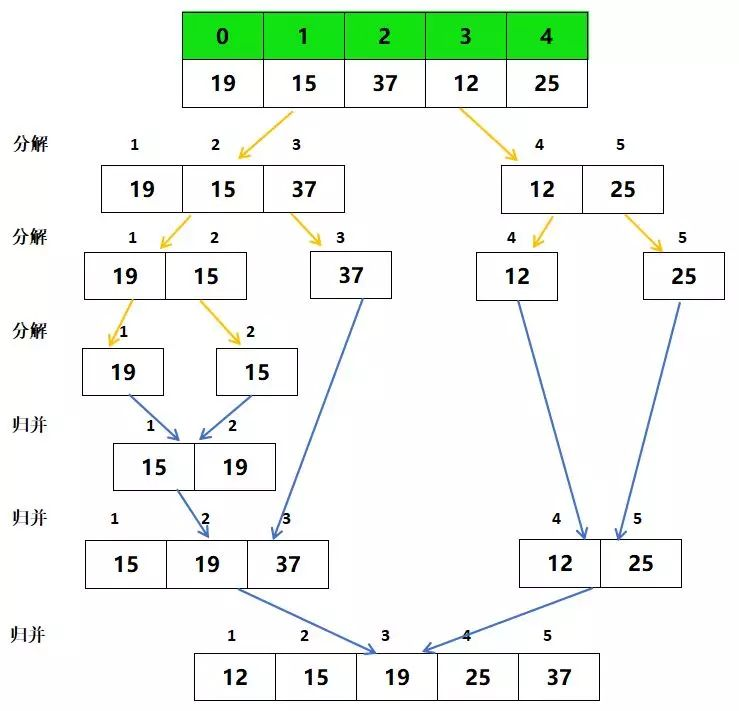
代码实现
import java.util.Arrays; public class MergeSort { public static int[] mergeSort(int[] arr) { int len = arr.length; if (len < 2) { return arr; } int mIdx = len / 2; return merge(mergeSort(Arrays.copyOfRange(arr, 0, mIdx)), mergeSort(Arrays.copyOfRange(arr, mIdx, len))); } private static int[] merge(int[] arrLeft, int[] arrRight) { int leftLen = arrLeft.length, rightLen = arrRight.length, leftIdx = 0, rightIdx = 0, idx = 0; int[] result = new int[leftLen + rightLen]; while (leftIdx < leftLen && rightIdx < rightLen) { if (arrLeft[leftIdx] < arrRight[rightIdx]) { result[idx++] = arrLeft[leftIdx++]; } else { result[idx++] = arrRight[rightIdx++]; } } while (leftIdx < leftLen) { result[idx++] = arrLeft[leftIdx++]; } while (rightIdx < rightLen) { result[idx++] = arrRight[rightIdx++]; } return result; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
6、快速排序(Quick Sort)
算法步驟
- 从序列中随机挑出一个元素,做为基准(pivot,这里选择序列的最左边元素作为基准);
- 重新排列序列,将所有比基准值小的元素摆放在基准前面,所有比基准值大的摆在基准的后面。该操作结束之后,该基准就处于数列的中间位置。这个操作称为分区(partition);
- 递归地把小于基准值元素的子序列和大于基准值元素的子序列进行上述操作即可。
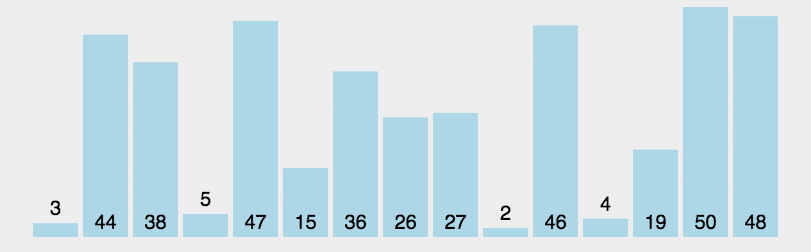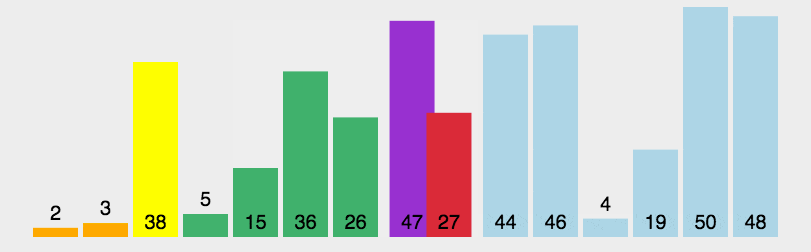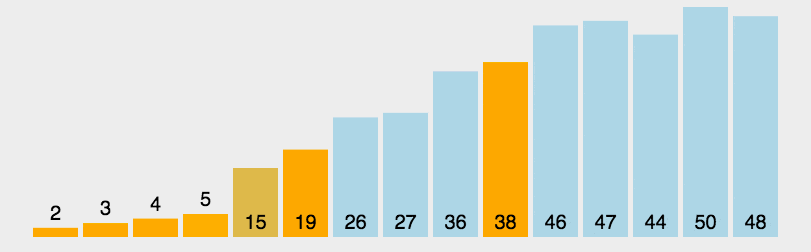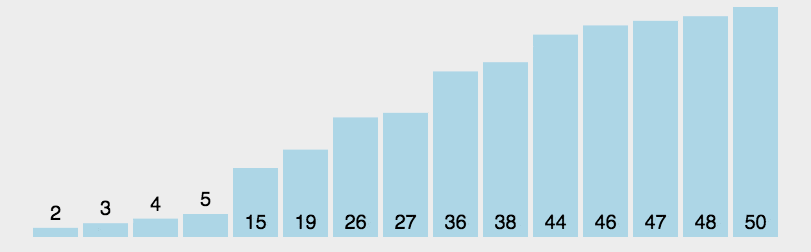
代码实现
public class QuickSort { public static void quickSort(int[] arr) { sort(arr, 0, arr.length - 1); } private static void sort(int[] arr, int left, int right) { if (left < right) { int pivotIdx = partition(arr, left, right); sort(arr, 0, pivotIdx - 1); sort(arr, pivotIdx + 1, right); } } private static int partition(int[] arr, int left, int right) { int idx = left + 1; for (int i = idx; i <= right; i++) { if (arr[left] > arr[i]) { swap(arr, i, idx++); } } swap(arr, left, idx - 1); return idx - 1; } private static void swap(int[] arr, int idx1, int idx2) { int tmp = arr[idx1]; arr[idx1] = arr[idx2]; arr[idx2] = tmp; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
7、堆排序(Heap Sort)
算法步驟
- 将待排序列(R0, R1, ……, Rn)构建成最大堆(最小堆);
- 将堆顶元素R[0]与最后一个元素R[n]进行交换,此时得到新的无序区(R0, R1, ……, Rn-1)和新的有序区(Rn),且满足R[0, 1, ……, n-1]<=R[n](>=R[n]);
- 由于调整后的新堆可能违反堆的性质,因此需要对当前无序区(R0, R1, ……, Rn-1)进行调整;
- 重复步骤2~3直到有序区的元素个数为n。

代码实现
public class HeapSort { private static int heapLen; public static void heapSort(int[] arr) { heapLen = arr.length; for (int i = heapLen - 1; i >= 0; i--) { heapify(arr, i); } for (int i = heapLen - 1; i > 0; i--) { swap(arr, 0, heapLen - 1); heapLen--; heapify(arr, 0); } } private static void heapify(int[] arr, int idx) { int left = idx * 2 + 1, right = idx * 2 + 2, largest = idx; if (left < heapLen && arr[left] > arr[largest]) { largest = left; } if (right < heapLen && arr[right] > arr[largest]) { largest = right; } if (largest != idx) { swap(arr, largest, idx); heapify(arr, largest); } } private static void swap(int[] arr, int idx1, int idx2) { int tmp = arr[idx1]; arr[idx1] = arr[idx2]; arr[idx2] = tmp; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
8、计数排序(Counting Sort)
算法步驟
- 找出数组中的最大值maxVal和最小值minVal;
- 创建一个计数数组countArr,其长度是maxVal-minVal+1,元素默认值都为0;
- 遍历原数组arr中的元素arr[i],以arr[i]-minVal作为countArr数组的索引,以arr[i]的值在arr中元素出现次数作为countArr[a[i]-min]的值;
- 遍历countArr数组,只要该数组的某一下标的值不为0则循环将下标值+minVal输出返回到原数组即可。
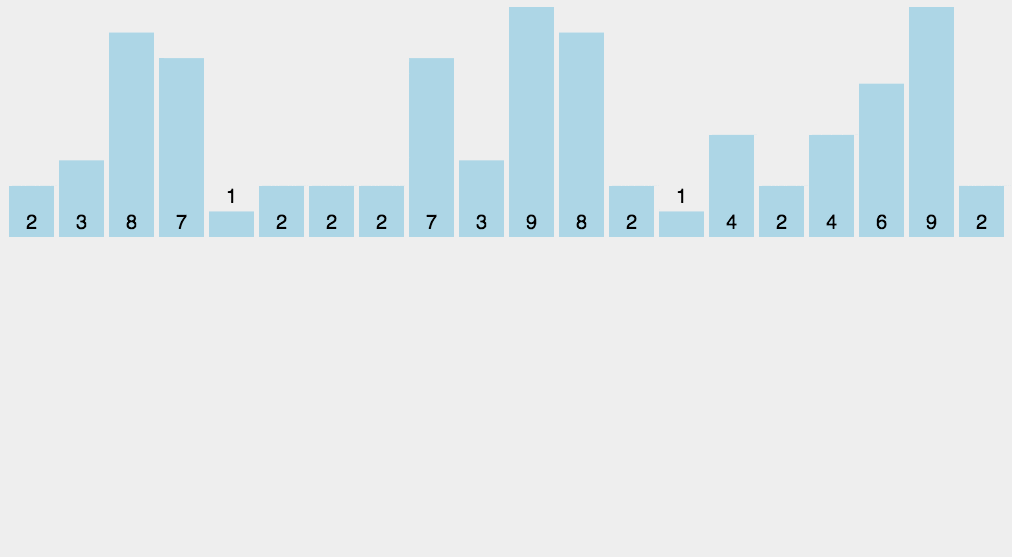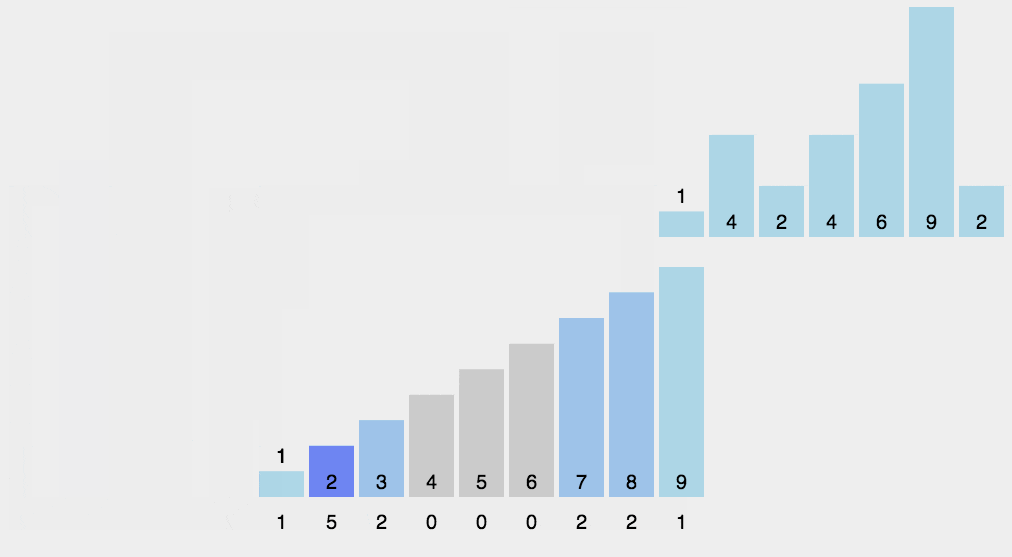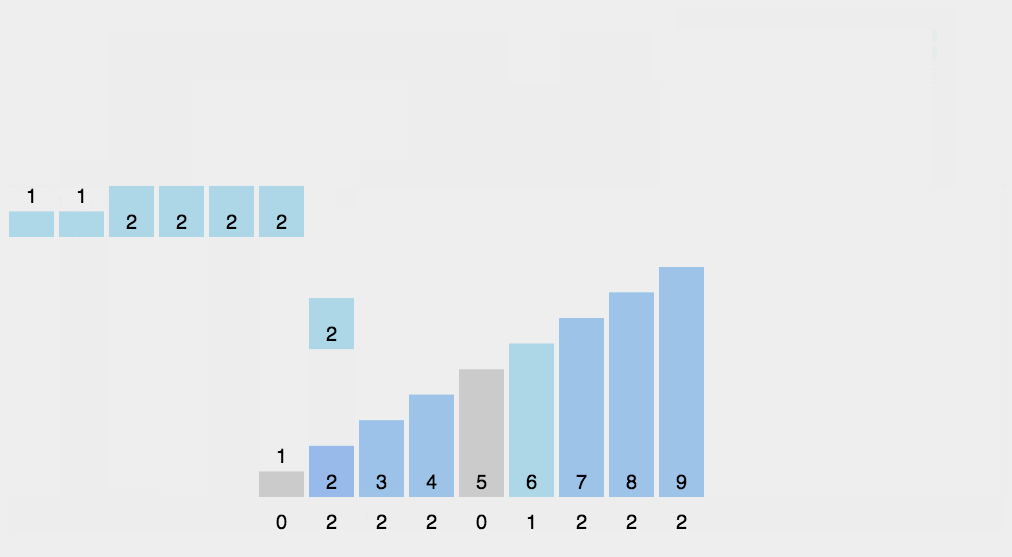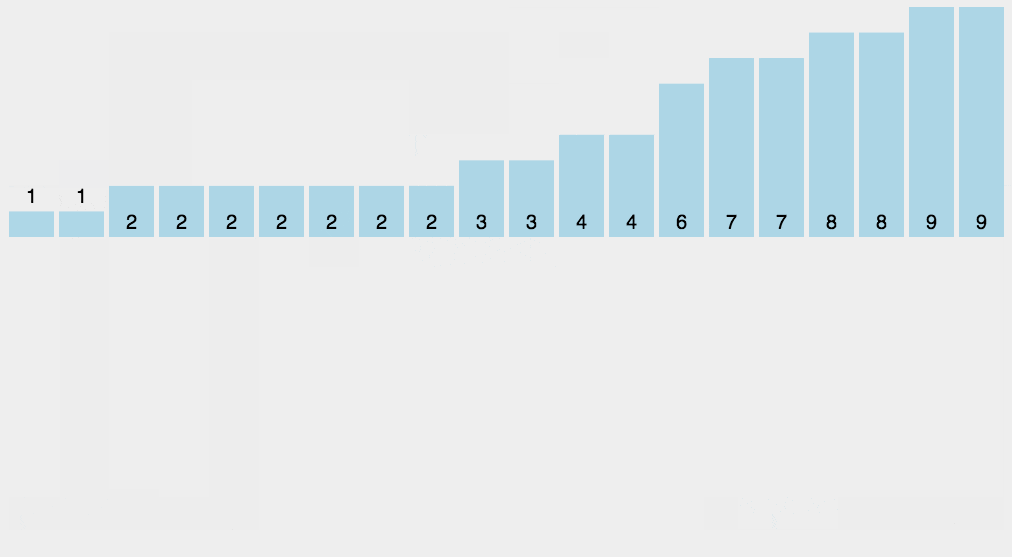
代码实现
public class CountingSort { public static void countingSort(int[] arr) { int len = arr.length; if (len < 2) return; int minVal = arr[0], maxVal = arr[0]; for (int i = 1; i < len; i++) { if (arr[i] < minVal) { minVal = arr[i]; } else if (arr[i] > maxVal) { maxVal = arr[i]; } } int[] countArr = new int[maxVal - minVal + 1]; for (int val : arr) { countArr[val - minVal]++; } for (int arrIdx = 0, countIdx = 0; countIdx < countArr.length; countIdx++) { while (countArr[countIdx]-- > 0) { arr[arrIdx++] = minVal + countIdx; } } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
9、桶排序(Bucket Sort)
算法步驟
- 设置一个bucketSize(该数值的选择对性能至关重要,性能最好时每个桶都均匀放置所有数值,反之最差),表示每个桶最多能放置多少个数值;
- 遍历输入数据,并且把数据依次放到到对应的桶里去;
- 对每个非空的桶进行排序,可以使用其它排序方法(这里递归使用桶排序);
- 从非空桶里把排好序的数据拼接起来即可。
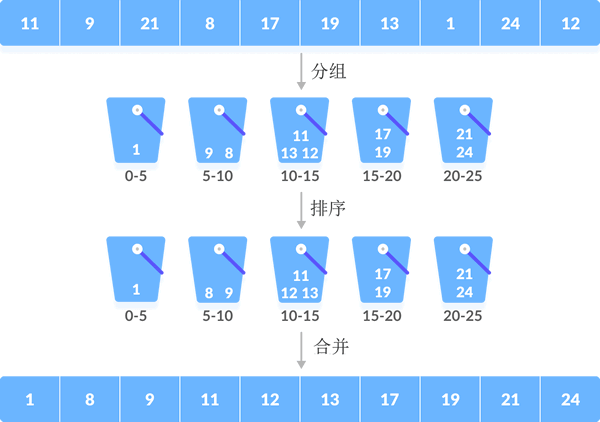
代码实现
import java.util.ArrayList; import java.util.List; public class BucketSort { private static List<Integer> bucketSort(List<Integer> arr, int bucketSize) { int len = arr.size(); if (len < 2 || bucketSize == 0) { return arr; } int minVal = arr.get(0), maxVal = arr.get(0); for (int i = 1; i < len; i++) { if (arr.get(i) < minVal) { minVal = arr.get(i); } else if (arr.get(i) > maxVal) { maxVal = arr.get(i); } } int bucketNum = (maxVal - minVal) / bucketSize + 1; List<List<Integer>> bucket = new ArrayList<>(); for (int i = 0; i < bucketNum; i++) { bucket.add(new ArrayList<>()); } for (int val : arr) { int idx = (val - minVal) / bucketSize; bucket.get(idx).add(val); } for (int i = 0; i < bucketNum; i++) { if (bucket.get(i).size() > 1) { bucket.set(i, bucketSort(bucket.get(i), bucketSize / 2)); } } List<Integer> result = new ArrayList<>(); for (List<Integer> val : bucket) { result.addAll(val); } return result; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
10、基数排序(Radix Sort)
算法步骤
- 取得数组中的最大数,并取得位数,即为迭代次数n(例如:数组中最大数为123,则 n=3);
- arr为原始数组,从最低位(或最高位)开始根据每位的数字组成radix数组(radix数组是个二维数组,其中一维长度为10),例如123在第一轮时存放在下标为3的radix数组中;
- 将radix数组中的数据从0下标开始依次赋值给原数组;
- 重复2~3步骤n次即可。

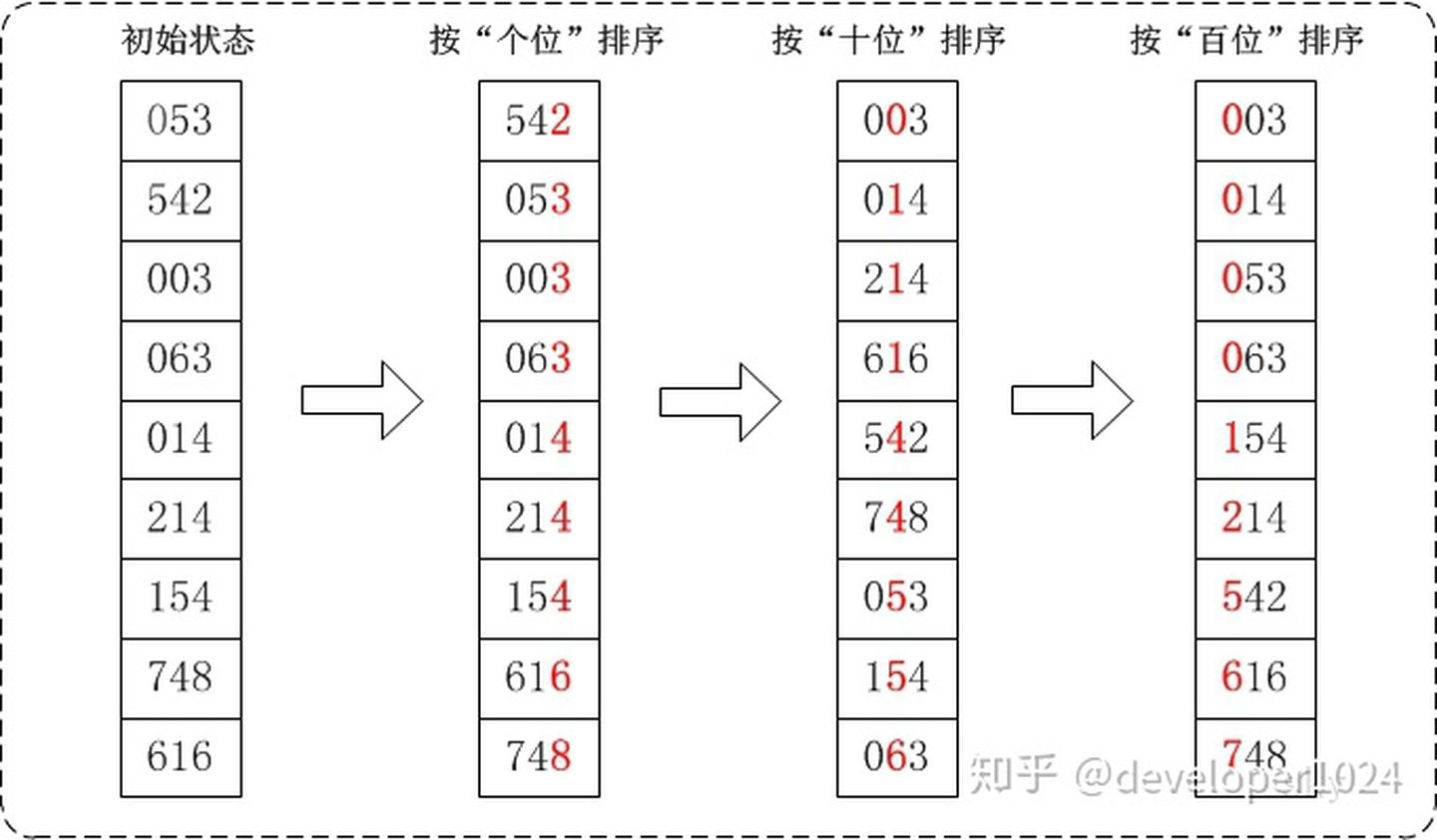
代码实现
import java.util.ArrayList; import java.util.List; //基数排序 public class RadixSort { public static void radixSort(int[] arr) { if (arr.length < 2) return; int maxVal = arr[0];//求出最大值 for (int a : arr) { if (maxVal < a) { maxVal = a; } } int n = 1; while (maxVal / 10 != 0) {//求出最大值位数 maxVal /= 10; n++; } for (int i = 0; i < n; i++) { List<List<Integer>> radix = new ArrayList<>(); for (int j = 0; j < 10; j++) { radix.add(new ArrayList<>()); } int index; for (int a : arr) { index = (a / (int) Math.pow(10, i)) % 10; radix.get(index).add(a); } index = 0; for (List<Integer> list : radix) { for (int a : list) { arr[index++] = a; } } } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
11、总结
数据量规模较小,考虑插入或选择。当元素分布有序时插入将大大减少比较和移动记录的次数,如果不要求稳定性,可以使用选择,效率略高于插入;
数据量规模中等,使用希尔排序;
数据量规模较大,考虑堆排序(元素分布接近正序或逆序)、快速排序(元素分布随机)和归并排序(稳定性);
一般来说不使用冒泡。
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/正经夜光杯/article/detail/759098
推荐阅读
相关标签



