devbox
木道寻08
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

【数据结构初阶】十一、归并排序(比较排序)的讲解和实现（递归版本 + 非递归版本 -- C语言实现）

作者：木道寻08 | 2024-07-26 06:06:49

赞

踩

【数据结构初阶】十一、归并排序(比较排序)的讲解和实现（递归版本 + 非递归版本 -- C语言实现）

=========================================================================

相关代码gitee自取：

C语言学习日记: 加油努力 (gitee.com)

 =========================================================================

接上期：

【数据结构初阶】十、快速排序(比较排序)讲解和实现
（三种递归快排版本 + 非递归快排版本 -- C语言实现）-CSDN博客

 =========================================================================

                     

常见排序算法的实现（续上期）

（详细解释在图片的注释中，代码分文件放下一标题处）
                 

四、归并排序

基本思想：

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法，
该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。
将已有序的子序列合并，得到完全有序的序列；
即先使每个子序列有序，再使子序列段间有序。
若将两个有序表合并成一个有序表，称为二路归并。

             

归并排序核心步骤：

                      

归并排序的特性总结：
  • 归并的缺点在于需要O(N)的空间复杂度，
    归并排序的思考更多的是解决在磁盘中的外排序问题
                      
  • 该算法时间复杂度：O(N*logN)
                         
  • 该算法空间复杂度：O(N)
                        
  • 该算法稳定性：稳定
                           

---------------------------------------------------------------------------------------------

                       

_MergeSort函数
--
归并排序函数(递归版本)的子函数(内部函数)， 完成归并操作

  • 之后会涉及递归操作，这里先设置递归结束条件：
    当前区间分割成无意义或不合理区间时，返回上层递归
                        
  • 因为要将当前区间分为两部分，所以先获得当前区间的中间下标mid
                      
  • 通过mid对当前区间的左区间进行递归，分割出新的左右区间
    同理，对当前区间的右区间也进行递归，分割出新的左右区间
                    
  • 递归分割完区间后，递归返回时再进行归并操作，
    将分割出的区间元素归并排序后放到动态开辟的tmp数组中，
    归并完成后再拷贝到原数组中
                 
  • 先定义当前区间的左右区间范围，
    再定义一个tmp数组的起始下标index
                   
  • 使用while循环将分割出的区间元素归并到tmp数组中
                     
  • 最后将归并好的tmp数组拷贝回原数组中
图示：

该函数执行逻辑图：

                          

                          
---------------------------------------------------------------------------------------------

                    

MergeSort函数 -- 归并排序函数（递归版本）

  • 开辟动态数组tmp：
    连续开辟和待排序数组对应类型和个数的动态空间
                   
  • 调用_MergeSort子函数进行归并操作
                    
  • 执行完归并排序后，释放开辟的动态空间tmp数组
图示：

该函数测试：

                          

                          
---------------------------------------------------------------------------------------------

                    

（难）MergeSortNonR函数 -- 归并排序函数（非递归版本）

  • 开辟动态数组tmp：
    连续开辟和待排序数组对应类型和个数的动态空间
                   
  • 因为不能使用递归进行“归并前分割”操作来分割区间，
    所以需要定义一个gap值
                    
  • gap默认为1，来进行“一一归二”；
    之后gap*2，进行“二二归四”；再gap*2，进行“四四归八”……
    使用while循环循环进行“几几归2*几”，
    完成本次while循环后，调整gap值（gap*=2*gap），
    进行下次当前gap值的“几几归2*几”操作
                     
  • 内嵌for循环，找到要进行归并的两个“小区间”，
    并确保这两个区间范围不会越界或按需对其进行修正（重点），
    然后进行归并操作和拷贝操作
                       
  • 退出while循环后，完成非递归归并排序，释放掉tmp数组
图示：

该函数测试：

                     

                     

                    

补充：计数排序（非比较排序）

             

本期博客再包含前两期博客中：
                    

【数据结构初阶】九、五种比较排序的讲解和实现
（直接插入 \ 希尔 \ 直接选择 \ 堆 \ 冒泡 -- C语言）-CSDN博客
                          

【数据结构初阶】十、快速排序(比较排序)讲解和实现
（三种递归快排版本 + 非递归快排版本 -- C语言实现）-CSDN博客

                     

我们总共了解了七种比较排序，

（比较排序即需要通过比较元素之间的大小来进行排序的排序算法）

                  

先通过下表来总结前面的七种比较排序：
排序算法
（比较排序）		平均情况
（时间复杂度）		最好情况
（时间复杂度）		最坏情况
（时间复杂度）		空间复杂度稳定性
直接插入排序O(N^2)O(N)O(N^2)O(1)稳定
希尔排序O(N*logN) ~ O(N^2)O(N^1.3)O(N^2)O(1)不稳定
直接选择排序O(N^2)O(N^2)O(N^2)O(1)不稳定
堆排序O(N*logN)O(N*logN)O(N*logN)O(1)不稳定
冒泡排序O(N^2)O(N)O(N^2)O(1)稳定
快速排序O(N*logN)O(N*logN)O(N^2)O(logN) ~ O(N)不稳定
归并排序O(N*logN)O(N*logN)O(N*logN)O(N)稳定

                  

再补充了解一种非比较排序：计数排序

基本思想：

计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用

                   

计数排序核心步骤：
  • 统计相同元素出现的次数
                      
  • 根据统计的结果将序列回收到原来的序列中
                     
归并排序的特性总结：
  • 计数排序在数据范围集中时，效率很高，但是适用范围及场景有限
                      
  • 该算法时间复杂度：O(MAX(N,range))
                         
  • 该算法空间复杂度：O(range)
                        

---------------------------------------------------------------------------------------------

                       

CountSort函数 -- 计数排序（鸽巢原理）函数

  • 先使用for循环找到a数组中的最大值max和最小值min
                       
  • 通过max和min获得数组a的元素范围range，
    开辟等大等数的动态统计数组count并检查开辟是否成功，
    开辟成功后对其进行初始化
                        
  • 使用for循环在统计数组count中统计对应下标元素出现次数
                        
  • 再根据统计的结果序列回收到原来的序列（数组）中
图示：

改函数执行逻辑图：

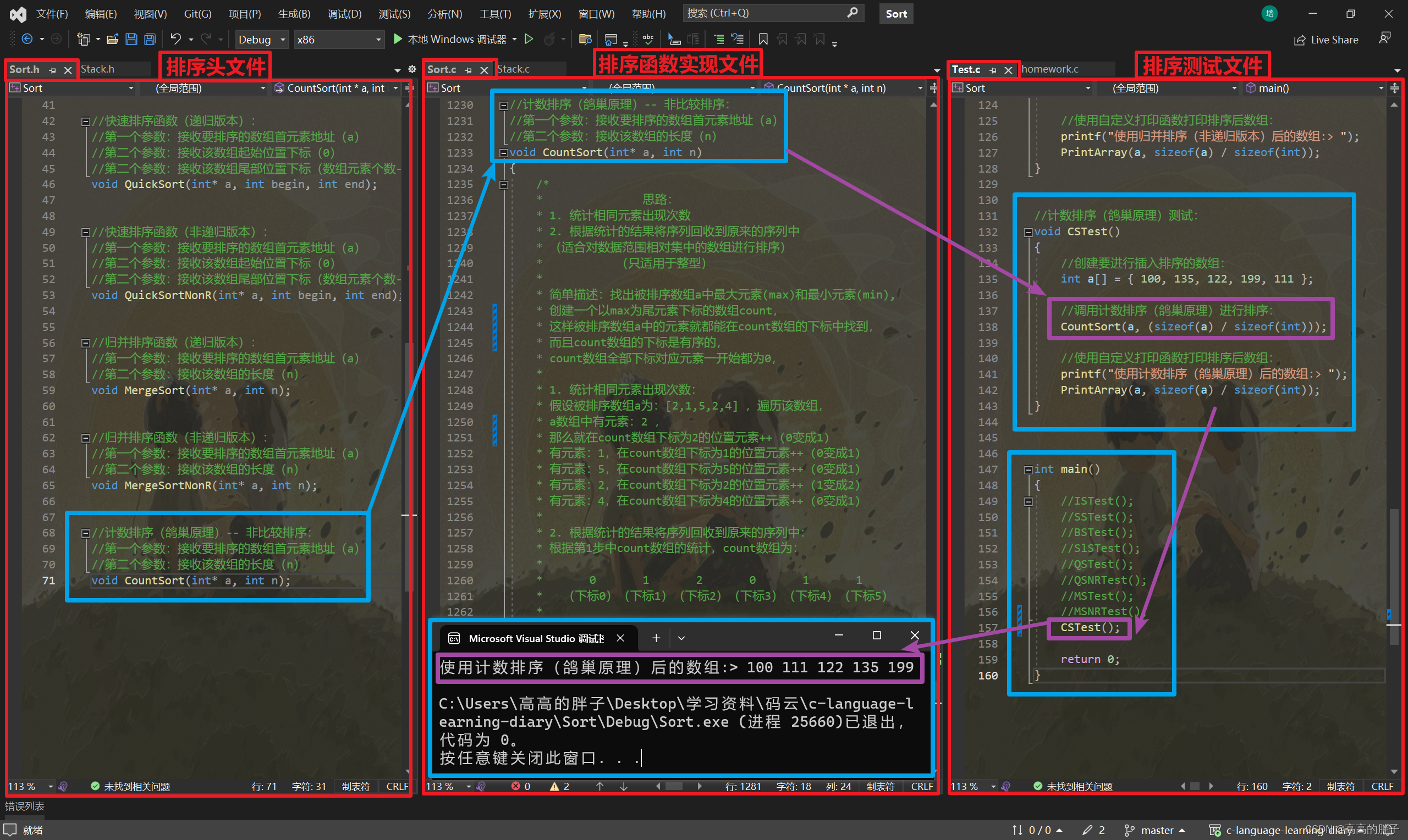
该函数测试：

         

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

             

对应代码（续上期）

Sort.h -- 排序头文件

  1. //归并排序函数（递归版本）：
  2. //第一个参数：接收要排序的数组首元素地址（a）
  3. //第二个参数：接收该数组的长度（n）
  4. void MergeSort(int* a, int n);
  5.  
  6.  
  7. //归并排序函数（非递归版本）：
  8. //第一个参数：接收要排序的数组首元素地址（a）
  9. //第二个参数：接收该数组的长度（n）
  10. void MergeSortNonR(int* a, int n);
  11.  
  12.  
  13. //计数排序（鸽巢原理）-- 非比较排序：
  14. //第一个参数：接收要排序的数组首元素地址（a）
  15. //第二个参数：接收该数组的长度（n）
  16. void CountSort(int* a, int n);

            

            

---------------------------------------------------------------------------------------------

             

Sort.c -- 排序函数实现文件

  1. //归并排序函数（递归版本）的子函数（内部函数）：
  2. //第一个参数：接收要排序的数组首元素地址（a）
  3. //第二个参数：接收开辟的等大动态空间首元素地址（tmp）
  4. //第三个参数：接收该数组起始位置下标（0）
  5. //第四个参数：接收该数组尾部位置下标（数组元素个数-1）
  6. //（函数名前加个“_”，表示为该函数的子函数）
  7. void _MergeSort(int* a, int* tmp, int begin, int end) 
  8. {
  9. 	//设置递归结束条件：
  10. 	if (end <= begin)
  11. 		//当前区间分割成无意义或不合理区间时：
  12. 	{
  13. 		//返回上层递归：
  14. 		return;
  15. 	}
  16.  
  17. 	//先获得当前区间的中间下标mid：
  18. 	int mid = (end + begin) / 2;
  19.  
  20. 	/*
  21. 	* 之后就可以将当前区间分成两个区间：
  22. 	* [begin, mid] [mid+1, end]
  23. 	* 如果左区间有序，右区间也有序就可以开展归并了
  24. 	* 
  25. 	* 可以先对当前有效的左区间进行递归，
  26. 	* 使其不断分割出新的左右区间；
  27. 	* 同理，也对当前右区间进行递归，不断分割出新的左右区间
  28. 	* 分割到区间范围： end <= begin 时（不合理、无意义区间），
  29. 	* 就返回递归不再分割
  30. 	* 
  31. 	* 递归分割完区间后，递归返回时再进行归并操作
  32. 	* 
  33. 	* 整个过程类似二叉树的后序遍历，左子树 -> 右子树 -> 根
  34. 	*								归并：
  35. 	* 左区间归并后有序 -> 右区间归并后有序 -> 归并排序后结果拷贝到原数组
  36. 	*/
  37.  
  38. 	//对当前区间的左区间进行递归，分割出新左右区间：
  39. 	_MergeSort(a, tmp, begin, mid); //分割后左区间范围：[begin, mid]
  40.  
  41. 	//对当前区间的右区间进行递归，分割出新左右区间：
  42. 	_MergeSort(a, tmp, mid+1, end); //分割后左区间范围：[mid+1, end]
  43.  
  44. 	/*
  45. 	* 递归分割完区间后，递归返回时再进行归并操作,
  46. 	* 将分割出的区间元素归并到动态开辟的tmp数组中，
  47. 	* 归并完成后再拷贝到原数组中：
  48. 	*/
  49.  
  50. 	//定义当前区间的左区间范围：
  51. 	int begin1 = begin; //当前左区间的左范围
  52. 	int end1 = mid; //当前左区间的右范围
  53.  
  54. 	//定义当前区间的右区间范围：
  55. 	int begin2 = mid+1; //当前右区间的左范围
  56. 	int end2 = end; //当前右区间的右范围
  57.  
  58. 	//再定义一个tmp数组的起始下标begin：
  59. 	int index = begin;
  60.  
  61. 	//使用whlie循环将分割出的区间元素归并tmp数组中：
  62. 	while (begin1 <= end1 && begin2 <= end2)
  63. 		//当前区间的左右区间范围合理：
  64. 	{
  65. 		/*
  66. 		* 比较当前a数组中当前区间的左右区间元素大小，
  67. 		* 将a数组当前区间中的较小值尾插放入tmp数组中（循环）
  68. 		*/
  69.  
  70. 		if (a[begin1] <= a[begin2])
  71. 			//如果当前区间的左区间元素小于等于其右区间元素：
  72. 		{
  73. 			tmp[index++] = a[begin1++];
  74. 			//将此时a数组中的当前区间的左区间元素尾插进tmp数组
  75. 			//放入后++调整位置
  76. 		}
  77. 		else
  78. 			//当前区间的右区间元素小于其左区间元素：
  79. 		{
  80. 			tmp[index++] = a[begin2++];
  81. 			//将此时a数组中的当前区间的右区间元素尾插进tmp数组
  82. 			//放入后++调整位置
  83. 		}
  84. 	}
  85.  
  86. 	/*
  87. 	* 当循环结束时，不知道是左右哪个区间不合理结束了，
  88. 	* 我们假设循环是左区间合理，右区间不合理而结束，
  89. 	* 那么此时的左区间就还有元素没尾插到tmp数组中，
  90. 	* 所以要将其剩下的元素再尾插到tmp数组中(右区间同理)：
  91. 	*/
  92.  
  93. 	//假设循环是左区间合理，右区间不合理而结束：
  94. 	while (begin1 <= end1)
  95. 		//当前左区间还合理(还有元素)：
  96. 	{
  97. 		//将其剩下的元素尾插进tmp数组中：
  98. 		tmp[index++] = a[begin1++];
  99. 	}
  100.  
  101. 	//如果循环是右区间合理，左区间不合理而结束：
  102. 	while (begin2 <= end2)
  103. 		//当前右区间还合理(还有元素)：
  104. 	{
  105. 		//将其剩下的元素尾插进tmp数组中：
  106. 		tmp[index++] = a[begin2++];
  107. 	}
  108.  
  109. 	/*
  110. 	* 到此就将元素都归并排序到了tmp数组中，
  111. 	* 最后还有将tmp数组拷贝到原数组中：
  112. 	*/
  113.  
  114. 	//使用memcpy库函数将归并好的tmp数组拷贝回原数组：
  115. 	memcpy(a + begin, tmp + begin, (end - begin + 1)*sizeof(int));
  116. 	//	   （目的地） （被拷贝位置）	       （拷贝数据大小）
  117. 	// end-begin+1, 即元素个数，因为区间左闭右闭所以还要+1
  118. }
  119.  
  120.  
  121. //归并排序函数（递归版本）：
  122. //第一个参数：接收要排序的数组首元素地址（a）
  123. //第二个参数：接收该数组的长度（n）
  124. void MergeSort(int* a, int n)
  125. {
  126. 	//开辟动态数组tmp：
  127. 	//连续开辟和待排序数组对应类型和个数的动态空间：
  128. 	int* tmp = (int*)malloc(sizeof(int) * n);
  129. 	//检查开辟动态空间是否成功：
  130. 	if (tmp == NULL)
  131. 		//返回NULL，说明开辟失败：
  132. 	{
  133. 		//打印错误信息：
  134. 		perror("malloc fail");
  135. 		//返回结束当前函数
  136. 		return;
  137. 	}
  138. 	
  139. 	/*
  140. 	* 之后要进行归并排序，需要使用递归进行，
  141. 	* 而上面代码是开辟动态空间，
  142. 	* 如果在本函数中使用递归进行归并排序操作，
  143. 	* 不断递归会不断地开辟动态空间，
  144. 	* 所以接下来的归并排序操作可以交给子函数进行：
  145. 	*/
  146.  
  147. 	//调用子函数进行归并排序操作：
  148. 	_MergeSort(a, tmp, 0, n - 1);
  149. 	//第一个参数：接收要排序的数组首元素地址（a）
  150. 	//第二个参数：接收开辟的等大动态空间首元素地址（tmp）
  151. 	//第三个参数：接收该数组起始位置下标（0）
  152. 	//第四个参数：接收该数组尾部位置下标（数组元素个数-1）
  153. 	//（函数名前加个“_”，表示为该函数的子函数）
  154.  
  155. 	//执行完归并排序后，释放开辟的动态空间：
  156. 	free(tmp);
  157. }
  158. //空间复杂度：O(N)
  159. //时间复杂度：O(N*logN)
  160.  
  161.  
  162.  
  163. //归并排序函数（非递归版本）：
  164. //第一个参数：接收要排序的数组首元素地址（a）
  165. //第二个参数：接收该数组的长度（n）
  166. void MergeSortNonR(int* a, int n)
  167. {
  168. 	/*
  169. 	*					思路：
  170. 	* 
  171. 	* 递归版本的归并排序是先通过递归将原数组不断分割，
  172. 	* 分割到无法分割后再进行归并排序操作返回到原数组，
  173. 	* 
  174. 	* 而非递归版本的归并排序要在一开始就找到原数组的
  175. 	* 最小区间，对两个最小区间进行归并操作，
  176. 	* 排序完成一个由两个最小区间组成“大区间”（已有序），
  177. 	* 最小区间都组成“大区间”后，
  178. 	* 再对两个“大区间”进行归并操作，组成一个“大大区间”（已有序）
  179. 	*				 （以此类推）
  180. 	* 其中组成“大区间”的“小区间”需要定义一个gap值来控制
  181. 	*（此过程就是递归版本中开始返回进行归并排序的过程）
  182. 	*（两区间有序了才能进行归并合成一个有序的大区间）
  183. 	*/
  184.  
  185. 	//开辟动态数组tmp：
  186. 	//连续开辟和待排序数组对应类型和个数的动态空间：
  187. 	int* tmp = (int*)malloc(sizeof(int) * n);
  188. 	//检查开辟动态空间是否成功：
  189. 	if (tmp == NULL)
  190. 		//返回NULL，说明开辟失败：
  191. 	{
  192. 		//打印错误信息：
  193. 		perror("malloc fail");
  194. 		//返回结束当前函数
  195. 		return;
  196. 	}
  197.  
  198. 	//gap = 1时，“一一归二”（11归并）：
  199. 	/*
  200. 	*			“一一归二”：
  201. 	* 控制一个区间的左右区间都各只有一个元素，
  202. 	* 再比较左右区间中元素（此时都只有一个元素）大小，
  203. 	* 进行归并操作将这左右区间归并为一个有两个元素的区间（已排序）
  204. 	* 
  205. 	* gap = 2时，“二二归四”（22归并）同理；
  206. 	* gap = 4时，“四四归八”（44归并）同理。
  207. 	*	（gap每次调整都是二倍的关系）
  208. 	*/
  209.  
  210. 	int gap = 1; //定义gap值
  211.  
  212. 	//最外层while循环控制“几几归”：
  213. 	while (gap < n)
  214. 	//当“几”>数组长度时，归并排序完成
  215. 	{
  216. 		for (int i = 0; i < n; i += 2 * gap)
  217. 			/*
  218. 			*		 循环变量修正表达式：i += 2*gap
  219. 			* 使用该循环变量修正表达式是为了确保
  220. 			* 除了第一次之后的定义左右区间能够定义正确，
  221. 			* 左右区间被归并成一个区间后，就不需要再被进行归并了，
  222. 			* 所以要调整循环变量修正表达式，保证一个区间不会被多次归并
  223. 			*/
  224. 		{
  225. 			/*
  226. 			* gap为1，那么就需要在当前区间中，
  227. 			* 从左往右依次以2个元素定义一个区间，
  228. 			* 将该区间再分割为左右两个区间，
  229. 			* 所以左右区间都各只有1个元素；
  230. 			*
  231. 			* gap为2 同理，在当前区间中，
  232. 			* 从左往右依次以4个元素定义一个区间，
  233. 			* 将该区间再分割为左右两个区间，
  234. 			* 所以左右区间都各只有2个元素；
  235. 			*
  236. 			*	    （以此类推）
  237. 			*/
  238.  
  239. 			//定义左区间的左范围（下标）：
  240. 			int begin1 = i;
  241. 			//定义左区间的右范围（下标）：
  242. 			int end1 = i + gap - 1;
  243.  
  244. 			//定义右区间的左范围（下标）：
  245. 			int begin2 = i + gap;
  246. 			//定义右区间的右范围（下标）：
  247. 			int end2 = i + 2 * gap - 1;
  248.  
  249. 			//[begin1, end1] [begin2, end2]
  250.  
  251. 			//判断以当前gap值划分的“左右区间”是否合理（会不会越界）：
  252. 			if (end1 >= n || begin2 >= n)
  253. 				/*
  254. 				*		    左右区间：
  255. 				* [begin1, end1] [begin2, end2]
  256. 				* 
  257. 				*				 end1 >= n
  258. 				* 通过分析，随着gap的增大，begin1不可能会越界，
  259. 				* 而从end1开始后就有可能会越界了，
  260. 				* 如果end1都已经越界了的话，那就没必要再进行归并了，
  261. 				* 
  262. 				*				begin2 >= n
  263. 				* 也有可能“左区间”正常，“右区间”越界了，导致
  264. 				* “几几归2*几”的第二个“几（右区间）”没了，
  265. 				* 导致无法将两个“小区间”归并成“大区间”
  266. 				* 
  267. 				* （如果“当前右区间”左右范围都不合理，
  268. 				*	  这一组就不用进行归并操作了）
  269. 				*/
  270. 			{
  271. 				//如果满足其中一种情况就无法进行归并操作了，
  272. 				//直接break跳出内嵌for循环：
  273. 				break; 
  274. 			}
  275.  
  276. 			if (end2 >= n)
  277. 				/*
  278. 				* 如果只有"右区间"的右范围越界(end2 >= n)的话，
  279. 				* 那么说明“右区间”还有元素可以和“左区间”进行归并，
  280. 				* 所以要对此时的“右区间”的右范围进行修正:
  281. 				*/
  282. 			{
  283. 				end2 = n - 1; //修正到数组的尾元素下标位置
  284. 			}
  285.  
  286.  
  287. 			//打印查看归并时“几几归2*几”的过程：
  288. 			printf("当前 “%d%d归%d” 的区间:> ", gap, gap, 2 * gap);
  289. 			printf("[%d,%d]  [%d,%d]\n", begin1, end1, begin2, end2);
  290.  
  291. 		/*
  292. 		* 通过gap分出“想要的左右两个区间（a数组的）”后，
  293. 		* 对这左右两个区间进行和递归版本相同的归并操作，
  294. 		* 比较这两个区间后，将“较小区间”尾插进tmp数组，
  295. 		* 这两个区间在tmp数组中变得有序，将其再拷贝回原数组
  296. 		*/
  297.  
  298. 		//再定义一个tmp数组的起始下标begin：
  299. 			int index = i;
  300.  
  301. 			//使用whlie循环将分割出的区间元素归并tmp数组中：
  302. 			while (begin1 <= end1 && begin2 <= end2)
  303. 				//当前区间的左右区间范围合理：
  304. 			{
  305. 				/*
  306. 				* 比较当前a数组中当前区间的左右区间元素大小，
  307. 				* 将a数组当前区间中的较小值尾插放入tmp数组中（循环）
  308. 				*/
  309.  
  310. 				if (a[begin1] < a[begin2])
  311. 					//如果当前区间的左区间元素小于其右区间元素：
  312. 				{
  313. 					tmp[index++] = a[begin1++];
  314. 					//将此时a数组中的当前区间的左区间元素尾插进tmp数组
  315. 					//放入后++调整位置
  316. 				}
  317. 				else
  318. 					//当前区间的右区间元素小于其左区间元素：
  319. 				{
  320. 					tmp[index++] = a[begin2++];
  321. 					//将此时a数组中的当前区间的右区间元素尾插进tmp数组
  322. 					//放入后++调整位置
  323. 				}
  324. 			}
  325.  
  326. 			/*
  327. 			* 当循环结束时，不知道是左右哪个区间不合理结束了，
  328. 			* 我们假设循环是左区间合理，右区间不合理而结束，
  329. 			* 那么此时的左区间就还有元素没尾插到tmp数组中，
  330. 			* 所以要将其剩下的元素再尾插到tmp数组中(右区间同理)：
  331. 			*/
  332.  
  333. 			//假设循环是左区间合理，右区间不合理而结束：
  334. 			while (begin1 <= end1)
  335. 				//当前左区间还合理(还有元素)：
  336. 			{
  337. 				//将其剩下的元素尾插进tmp数组中：
  338. 				tmp[index++] = a[begin1++];
  339. 			}
  340.  
  341. 			//如果循环是右区间合理，左区间不合理而结束：
  342. 			while (begin2 <= end2)
  343. 				//当前右区间还合理(还有元素)：
  344. 			{
  345. 				//将其剩下的元素尾插进tmp数组中：
  346. 				tmp[index++] = a[begin2++];
  347. 			}
  348.  
  349. 			//使用memcpy库函数将归并好的tmp数组拷贝回原数组：
  350. 			//（放在内嵌for循环中，归并一组就拷贝一组，没归并就不拷贝了）
  351. 			memcpy(a + i, tmp + i, (end2-i+1) * sizeof(int));
  352. 			//	（目的地)(被拷贝位置）   （拷贝数据大小）
  353. 			/*
  354. 			* end2-i+1, 即元素个数，这里“-i”本来应该是begin1，
  355. 			* 但是begin1在进行归并操作时会被++，所以应该是“-i”，
  356. 			* 即减去begin1的起始值i，再“+1”是因为“数组尾元素下标+1”
  357. 			* 才是数组的元素个数
  358. 			*/	
  359. 		
  360. 		} //内嵌for循环
  361.  
  362. 		//打印当前一组“几几归2*几”对应的所有区间后，
  363. 		//进行换行，准备下次“几几归2*几”：
  364. 		printf("\n");
  365.  
  366. 		//		“几几归2*几”：
  367. 		//“一一归二”后，进行“二二归四”，
  368. 		//“二二归四”后，进行“四四归八”，
  369. 		//（以此类推，直到“几”>数组长度）
  370. 		gap *= 2 ;
  371.  
  372. 		/*
  373. 		* 执行到此，以gap=1为准的归并操作就完成了，
  374. 		* 但是当前只能处理有2^n个元素的数组，
  375. 		* (如果不对归并的“左右区间”进行限定的话)
  376. 		* 不然归并会出各种问题，所以要在归并开始前进行判断，
  377. 		* 看用于归并的“左右区间”会不会越界
  378. 		*/
  379.  
  380. 	} //最外层while循环
  381. 	
  382. 	//执行完归并排序后，释放开辟的动态空间：
  383. 	free(tmp);
  384. }
  385. //时间复杂度：O(N*logN)
  386. //空间复杂度：O(N)
  387. //(时间和空间复杂度都和递归版本相同)
  388.  
  389.  
  390.  
  391. //计数排序（鸽巢原理）-- 非比较排序：
  392. //第一个参数：接收要排序的数组首元素地址（a）
  393. //第二个参数：接收该数组的长度（n）
  394. void CountSort(int* a, int n)
  395. {
  396. 	/*
  397. 	*				思路：
  398. 	* 1. 统计相同元素出现次数
  399. 	* 2. 根据统计的结果将序列回收到原来的序列中
  400. 	* （适合对数据范围相对集中的数组进行排序）
  401. 	*		    （只适用于整型）
  402. 	* 
  403. 	* 简单描述：找出被排序数组a中最大元素(max)和最小元素(min),
  404. 	* 创建一个以max为尾元素下标的数组count，
  405. 	* 这样被排序数组a中的元素就都能在count数组的下标中找到，
  406. 	* 而且count数组的下标是有序的，
  407. 	* count数组全部下标对应元素一开始都为0，
  408. 	* 
  409. 	* 1. 统计相同元素出现次数：
  410. 	* 假设被排序数组a为：[2,1,5,2,4] ，遍历该数组，
  411. 	* a数组中有元素：2 ，
  412. 	* 那么就在count数组下标为2的位置元素++ (0变成1)
  413. 	* 有元素：1，在count数组下标为1的位置元素++ (0变成1)
  414. 	* 有元素：5，在count数组下标为5的位置元素++ (0变成1)
  415. 	* 有元素：2，在count数组下标为2的位置元素++ (1变成2)
  416. 	* 有元素：4，在count数组下标为4的位置元素++ (0变成1)
  417. 	* 
  418. 	* 2. 根据统计的结果将序列回收到原来的序列中：
  419. 	* 根据第1步中count数组的统计，count数组为：
  420. 	*
  421. 	*		0		1		2		0		1		1
  422. 	*   （下标0）（下标1）（下标2）（下标3）（下标4）（下标5）
  423. 	*
  424. 	* 这时遍历count数组，按以下规律覆盖写到原数组a中：
  425. 	*
  426. 	*	0有0个，1有1个，2有2个，3有0个，4有1个，5有1个 
  427. 	*			（0个的话就不覆盖写了）
  428. 	*						↓
  429. 	*				a数组：1 2 2 4 5
  430. 	*/
  431.  
  432. 	//存储a数组（被排序数组）的最小值：
  433. 	int min = a[0]; //默认为首元素
  434.  
  435. 	//存储a数组（被排序数组）的最大值：
  436. 	int max = a[0]; //默认为首元素
  437.  
  438. 	//使用for循环找到a数组中的最小值和最大值：
  439. 	for (int i = 0; i < n; i++)
  440. 	{
  441. 		//找最小值：
  442. 		if (a[i] < min)
  443. 			//当前元素小于min：
  444. 		{
  445. 			min = a[i]; //将该元素赋给min
  446. 		}
  447.  
  448. 		//找最大值：
  449. 		if (a[i] > max)
  450. 			//当前元素大于max：
  451. 		{
  452. 			max = a[i]; //将该元素赋给max
  453. 		}
  454. 	}
  455.  
  456. 	//定义统计数组count的区间（元素个数）：
  457. 	int range = max - min + 1;
  458. 	// [min, max] 左闭右闭，所以元素个数还要+1
  459.  
  460. 	//为统计数组count开辟动态空间：
  461. 	int* count = (int*)malloc(sizeof(int) * range);
  462. 	//检查是否开辟成功：
  463. 	if (count == NULL)
  464. 		//开辟后返回空指针：
  465. 	{
  466. 		//说明开辟失败，打印错误信息：
  467. 		perror("malloc fail");
  468. 		//返回结束函数：
  469. 		return;
  470. 	}
  471.  
  472. 	//对统计数组进行初始化：
  473. 	memset(count, 0, sizeof(int) * range);
  474. 	//使用memset函数将count数组所有元素都初始化为0
  475.  
  476. 	// 1. 使用for循环统计相同元素出现次数：
  477. 	for (int i = 0; i < n; i++)
  478. 	{
  479. 		count[a[i] - min]++;
  480. 		/*
  481. 		* 这里count数组的下标写成：[a[i] - min]
  482. 		* 是为了实现 “相对映射” ：
  483. 		* 被排序数组a可能是：[100, 135, 122, 199, 111] 
  484. 		* 这里max为199，传统方式count数组就要开辟 [0, 199]
  485. 		* 200个空间，而实际只会使用 [100, 199] 这部分空间，
  486. 		* 所以上面 range = 199 - 100 + 1 = 100 只开辟了100个空间，
  487. 		* 但是开辟的100个空间，他的下标范围却是 [0, 99]
  488. 		* a数组中元素无法对应count数组的下标，所以就需要“相对映射”
  489. 		* 
  490. 		*					相对映射：
  491. 		*	a数组元素 - 节省开辟的空间数（这里是100） = 相对下标
  492. 		* 以元素100为例： 100 - 100 = 0 ，
  493. 		* 这时 a数组中的元素100 就对应 count数组中下标0，
  494. 		* a数组中每有一个元素100，count数组下标0元素++，
  495. 		* a数组中其它元素同理。到时进行恢复操作的时候再将
  496. 		* count下标 + 节省开辟的空间数（这里是100） 即可
  497. 		* （即 a数组中对应元素）
  498. 		*/
  499. 	}
  500.  
  501. 	// 2. 根据统计的结果将序列回收到原来的序列（数组）中：
  502.  
  503. 	int j = 0; //用于遍历a数组（原数组）下标
  504. 	
  505. 	for (int i = 0; i < range; i++)
  506. 		//range为数组元素所在范围（区间）
  507. 	{
  508. 		while (count[i]-- != 0)
  509. 			/*
  510. 			* count[i] 为统计数组的当前下标i元素，
  511. 			* 元素为几，说明该元素下标i在a数组中所对应的元素有几个，
  512. 			* 如果count数组中i下标元素为0，则不考虑该下标，
  513. 			* 这里是将i下标元素不为0的进行操作，
  514. 			* 将其i下标在a数组中对应的元素一一恢复：
  515. 			*/
  516. 		{
  517. 			a[j++] = i + min;
  518. 			/*
  519. 			* 因为我们使用了 "相对映射"
  520. 			* 所以 i下标 + 节省开辟的空间数 == a数组中对应元素
  521. 			*/
  522. 		}
  523. 	}
  524. }
  525. //时间复杂度：O(N + range)
  526. /*
  527. * 如果排序的数据比较集中，那么range会比较小 -- O(N)
  528. * 如果不集中，range会比较大 -- O(range)
  529. */
  530. //空间复杂度：O(range)

            

            

---------------------------------------------------------------------------------------------

             

Test.c -- 排序测试文件

  1. //归并排序（递归版本）测试：
  2. void MSTest()
  3. {
  4. 	//创建要进行插入排序的数组：
  5. 	int a[] = { 9,1,2,5,7,4,8,6,3,5 };
  6.  
  7. 	//调用快速排序（递归版本）进行排序：
  8. 	MergeSort(a, (sizeof(a) / sizeof(int)));
  9.  
  10. 	//使用自定义打印函数打印排序后数组：
  11. 	printf("使用归并排序（递归版本）后的数组:> ");
  12. 	PrintArray(a, sizeof(a) / sizeof(int));
  13. }
  14.  
  15.  
  16. //归并排序（非递归版本）测试：
  17. void MSNRTest()
  18. {
  19. 	//创建要进行插入排序的数组：
  20. 	int a[] = { 9,1,2,5,7,4,8,6,3,5 };
  21.  
  22. 	//调用快速排序（非递归版本）进行排序：
  23. 	MergeSortNonR(a, (sizeof(a) / sizeof(int)));
  24.  
  25. 	//使用自定义打印函数打印排序后数组：
  26. 	printf("使用归并排序（非递归版本）后的数组:> ");
  27. 	PrintArray(a, sizeof(a) / sizeof(int));
  28. }
  29.  
  30.  
  31. //计数排序（鸽巢原理）测试：
  32. void CSTest()
  33. {
  34. 	//创建要进行插入排序的数组：
  35. 	int a[] = { 100, 135, 122, 199, 111 };
  36.  
  37. 	//调用计数排序（鸽巢原理）进行排序：
  38. 	CountSort(a, (sizeof(a) / sizeof(int)));
  39.  
  40. 	//使用自定义打印函数打印排序后数组：
  41. 	printf("使用计数排序（鸽巢原理）后的数组:> ");
  42. 	PrintArray(a, sizeof(a) / sizeof(int));
  43. }
  44.  
  45.  
  46.  
  47. int main()
  48. {
  49. 	//ISTest();
  50. 	//SSTest();
  51. 	//BSTest();
  52. 	//SlSTest();
  53. 	//QSTest();
  54. 	//QSNRTest();
  55. 	//MSTest();
  56. 	//MSNRTest();
  57. 	CSTest();
  58.  
  59. 	return 0;
  60. }
本文内容由网友自发贡献，转载请注明出处：【wpsshop博客】
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号