【数据结构】图的最小生成树_图数据库 最小生成树

最小生成树

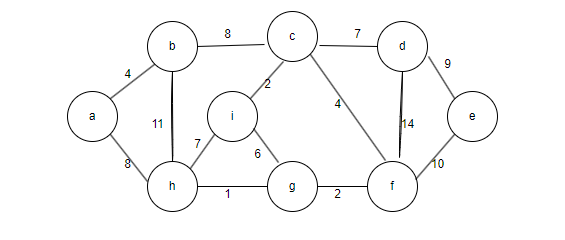
一个图中有N个顶点，边的数量一定是>=N-1，我们从中选取N-1条边，用来连接N个点，所形成的边权之和最小，就是最小生成树。

构成最小生成树的准则

1. 只能使用图中的边来构造最小生成树
2. 只能使用恰好n-1条边来连接图中的n个顶点
3. 选用的n-1条边不能构成回路

构成最小生成树的的方法：Kruskal(克鲁斯卡尔)算法和Prim(普里姆)算法

二者都是基于逐步贪心的算法

Kruskal算法

Kruskal算法的思路

1. 先构建出一个N个顶点的最小生成树图，其中不包含任何边，将原图的各个边按照权值进行排序
2. 在排序的边中，选出一条边，如果这条边不会与其它边构成环，就添加到最小生成树图里
3. 当选边数为N-1时，就构成最小生成树，否则不构成

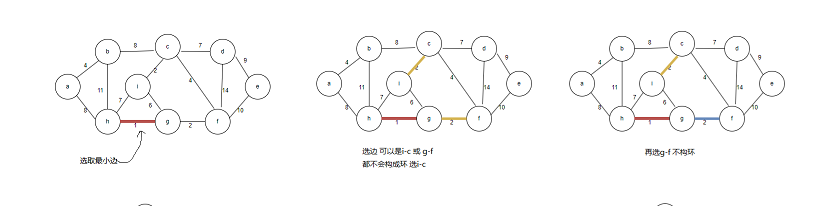
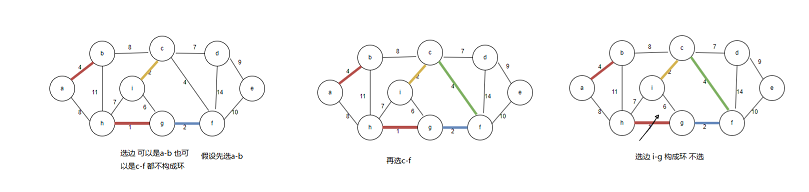
描述这一过程，构成最小生成树

再选边时 都会构成环，此时已经是n-1条边，连接n个顶点，是最小生成树。

• 要做选取最小的边，就需要将边的关系放到优先级队列中。每一个取边，就是top pop的过程。
• 判断是否成环，需要一个集合，如果顶点A和B都在集合中，那么就构成环。
• 只要优先级队列还有边就要一直判断选边，直到队列为空，如果最后选取了n-1条边，那么就是最小生成树，反之不是，并返回所有的权和。

		struct Edge
		{
			size_t _srci;
			size_t _dsti;
			W _w;
 
			Edge(size_t srci, size_t dsti, const W& w)
				:_srci(srci)
				, _dsti(dsti)
				, _w(w)
			{}
 
			bool operator>(const Edge& e) const
			{
				return _w > e._w;
			}
			bool operator<(const Edge& e) const
			{
				return _w < e._w;
			}
 
		};
 
		//最小生成树
		W Kruskal(Self& minTree)
		{
			size_t n = _vertexs.size();
			minTree._vertexs = _vertexs;
			minTree._vIndexMap = _vIndexMap;
			minTree._matrix.resize(n);
			for (size_t i = 0; i < minTree._vertexs.size(); i++)
			{
				minTree._matrix[i].resize(n, MAX_W);
			}
 
			//优先级队列
			priority_queue<Edge, vector<Edge>, greater<Edge>> minque;
			//把所有的边都放进去
			for (size_t i = 0; i < _matrix.size(); i++)
			{
				for (size_t j = 0; j < _matrix[i].size(); j++)
				{
					if (i<j&&_matrix[i][j] != MAX_W)
					{
						minque.push(Edge(i, j, _matrix[i][j]));
					}
				}
			}
 
			//选边
			W total = W();
			size_t i = 1;
			UnionFindSet ufs(_vertexs.size());
			while (!minque.empty())
			{
				Edge minedge = minque.top();
				minque.pop();
				
				if (!ufs.InSet(minedge._srci,minedge._dsti))
				{
					cout << _vertexs[minedge._srci] << "->" << _vertexs[minedge._dsti] << ":" << minedge._w << endl;
					ufs.Union(minedge._srci, minedge._dsti);
					
					minTree._AddEdge(minedge._srci, minedge._srci, minedge._w);
 
					total += minedge._w;
					++i;
				}
				
				else
				{
					cout << "构成环" << endl;
				}
			}
 
			if (i == _vertexs.size())
			{
				return total;
			}
			
			return W();
		}

1. 创建最小生成树的顶点和映射，提前为邻接矩阵开空间。
2. 遍历原图的邻接矩阵，将边都放到优先级队列中。
3. 选边时，只有不在同一个集合中，才被添加到最小生成树的边里。

对于自定义类型的优先级队列，需要自定比较函数。

这里也运用到并查集的知识。

---

Prim算法

算法的基本思路

• 构造一个含 n 个顶点、不含任何边的图作为最小生成树，将图中的顶点分为两个集合，X Y 集合中的顶点是已经连接到最小生成树中的顶点，Y集合中的顶点是还没有连接到最小生成树中的顶点，刚开始时X 集合中只包含给定的起始顶点。
• 每次从连接X 集合与 Y 集合的所有边中选出一条权值最小的边，将其加入到最小生成树中，由于选出来的边对应的两个顶点一个属于X 集合，另一个属于Y集合，因此是不会构成回路的。

步骤

1. 先创建最小生成树的图，构造顶点和下标映射，为邻接矩阵开辟空间。
2. 创建 X Y标记数组，X是已经包含的集合(全false)，Y是没有被包含的集合(true)。
3. 求出srci表示从哪一个顶点开始。X[srci]=true,Y[srci]=false
4. 将srci所有相邻的边都放到优先级队列中，遍历优先级队列，如果不构成环，就添加边
5. 然后将dsti的边相邻也添加到队列中
6. 确保不相邻的方法：srci在X中，dsti在Y中,就是不相邻

		W Prim(Self& minTree, const W& src)
		{
			size_t srci = GetVertexIndex(src);
			size_t n = _vertexs.size();
			
			minTree._vertexs = _vertexs;
			minTree._vIndexMap = _vIndexMap;
			minTree._matrix.resize(n);
			for (size_t i = 0; i < minTree._vertexs.size(); i++)
			{
				minTree._matrix[i].resize(n, MAX_W);
			}
 
			vector<bool> X(n, false);
			vector<bool> Y(n, true);
			X[srci] = true;
			Y[srci] = false;
 
			//优先级队列
			priority_queue<Edge, vector<Edge>, greater<Edge>> minque;
			//把所有的边都放进去
			for (size_t i = 0; i < _matrix.size(); i++)
			{
				if (  _matrix[srci][i] != MAX_W)
				{
						minque.push(Edge(srci, i, _matrix[srci][i]));
				}
			}
	
 
			cout << "Prim 选边" << endl;
			W total = W();
			size_t i = 1;
			while (!minque.empty())
			{
				Edge minedge = minque.top();
				minque.pop();
 
				if (X[minedge._dsti])
				{
					//cout << "构成环";
				}
				else
				{
					minTree._AddEdge(minedge._srci, minedge._dsti, minedge._w);
					X[minedge._dsti] = true;
					Y[minedge._dsti] = false;
					++i;
					total += minedge._w;
					
					if (i == n)		break;
 
					//将dsti相邻的都放到队列中
					for (size_t index = 0; index < n; index++)
					{
						if (Y[index]&&_matrix[minedge._dsti][index] != MAX_W)
						{
							minque.push(Edge(minedge._dsti, index,_matrix[minedge._dsti][index]));
						}
					}
				}
			}
			if (i == n)
			{
				return total;
			}
			return W();
		}

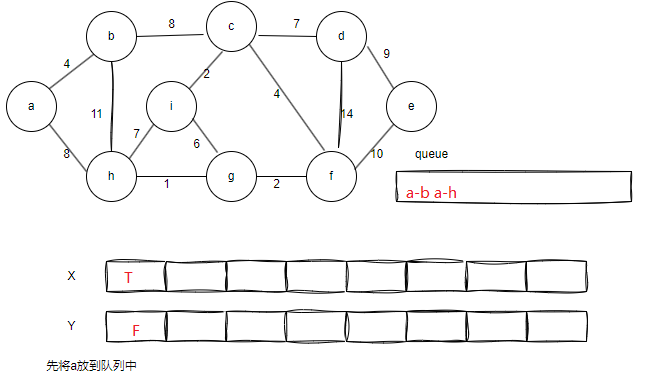
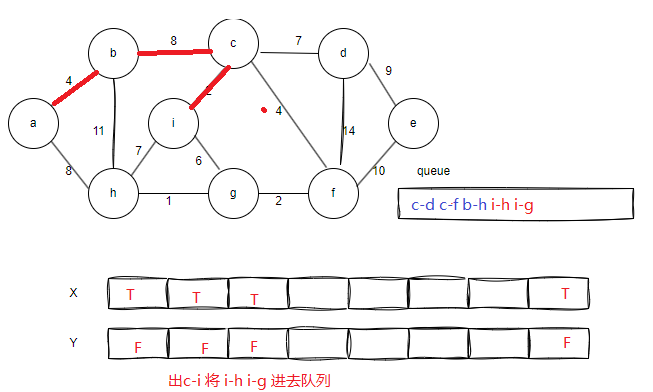
画图演示这个过程

........省略几步类似的步骤

选择 i-g  i-h a-h时都会成环，不操作

最终的结果

最后依旧需要判断，如果完成n-1次选边后，可以构成最小生成树

否则，无法构成

---

Prim算法每次选边都会遍历相邻的边，是时间复杂度较大的算法。

Kruskal是全局贪心，每次选边都是选择最小的边。

Prim算法是局部贪心，总是选择目前相连的最小边。

二者所得到的权值是一样的。