- 1【STM32F407学习笔记】时钟树和SysTick精准延时_stm32f407时钟树
- 2安恒“网安铁三角”:守护数字世界的实战宝典
- 3NLP-新闻文本分类(六、基于深度学习的文本分类3_class sentencoder(nn.module):
- 4Hadoop——HDFS文件系统的Java API操作(上传、下载、查看、删除、创建文件)详细教学_java hdfs上传文件使用教程 hadoop.home.dir
- 5Android串口开发基于ndk简书,Android studio 配置NDK开发
- 6Arduino(NodeMcu)上传程序时出现“上传错误:exit status 2”
- 7vue加载中展示【nprogress(进度条)&Lottie(动画)】_进度条的lottie文件
- 8基于FPGA的正弦PWM产生系统verilog实现_怎么用正弦波产生pwm
- 9自然语言处理之word2vec_word2vec 困惑度
- 10《人工智能技术在网络安全方向的应用》学习笔记_人工智能在网络安全的应用关键词
非递归算法——快速排序、归并排序
赞
踩
哈喽大家好,我是保护小周ღ,本期为大家带来的是常见排序算法中的快速排序、归并排序,非递归算法,分享所有源代码,粘贴即可运行,保姆级讲述,包您一看就会,快来试试吧~

目录
1.1 栈是什么,数据结构“栈”又是什么,他们之间有什么区别?
一、递归的缺陷
递归的缺陷:如果栈帧深度太深(递归的次数多),栈空间不够用(大概只有几兆)可能会溢出。
一般校招可能考察的就是非递归算法,知道你会递归算法,偏偏考你非递归,您能咋办呐,多学点呗,运筹帷幄,方能立于不败之地。
递归改非递归的方法:
- 直接改循环(简单一点的递归)
- 借助数据结构的“栈”模拟递归过程(复杂一点的递归)
1.1 栈是什么,数据结构“栈”又是什么,他们之间有什么区别?


函数调用建立栈帧,栈帧中存储局部变量,参数等等。
栈区,堆区等是操作系统这门学科中对内存的划分,数据结构的“栈”,“堆”是存放、处理数据的一种结构,跟内存的栈区,堆区,没有啥关系,但是有一点,数据结构的“栈”和内存的栈区都是后进先出。
1.2 C/C++ 程序内存分配的几个区域:
1.栈区(stack):在执行函数时,函数内局部变量的存储单元都可以在栈上创建,函数执行结束时这些存储单元自动释放。栈内存分配运算内置于处理器的指令集中,效率很高,但是分配的内存容量有限,栈区主要存放运行函数而分配的局部变量,函数参数,返回数据,返回地址等。
2.堆区(heap):一般由程序员分配释放,若程序员不释放,程序结束时由OS回收。
3.数据段(静态区)(static)存放全局变量,静态变量。程序结束后由系统释放。
4.代码段:存放函数体(类成员函数和全局函数)的二进制代码
二、快排非递归算法
快速排序(Quicksort)是Hoare于1962年提出的一种二叉树结构的交换排序方法,有时候也叫做划分交换排序,是一个高效的算法,其基本思想为:任取待排序 元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有 元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所 有元素都排列在相应位置上为止。这是一个分治算法,而且它就在原地交换数据排序。
如果大家对快速排序的逻辑,递归算法还不熟悉的朋友可以观看博主的另一篇博客,快排递归算法分享了三种方法:挖坑法,左右指针法,前后指针法,以及两种优化方式:解决快排最坏情况的“三数取中”,避免递归次数过多的"小区间优化"。
常见排序算法之交换排序——冒泡排序、快速排序_保护小周ღ的博客-CSDN博客
2.1 算法思想
借助数据结构的“栈”模拟递归过程,原理其实跟递归差不多,只是不是由操作系统自己建立栈帧,同时堆区上的空间是够的。我们分割的区间其实是由数据结构“栈”帮我们保存起来了,出栈区间,循环执行单趟排,这就是模拟递归的原理。

用一组数据,简单的让大家了解了一下,模拟递归是个咋回事。
2.2 程序实现
首先咱们要写个栈,不要慌,博主稍后会在后面附上栈的完整代码,没办法,谁叫C语言没有自己的库嘞,C++,Java,库里都有栈。
以博主使用的编译器为例:启动 Visual Studio 2019,创建新项目——>空项目——>创建项目名称,选择保存地址,然后我们打开解决方案资源管理器,找到源文件,添加以下三个文件(文件名不定,关于栈的程序博主已经写好了)。
Stack.h ——关于程序相关函数的声明,符号声明,头文件包含等(栈)
Stack.c—— 程序相关函数的实现(栈)
QuickSort.c ——程序的逻辑(非递归快排)

QuickSort.c
- #include"Stack.h"//引用一手我们自己写的头文件,不要用<>,这个是引用库里的
-
- //挖坑法单趟排
- int QuickSort(int* a, int left, int right)//升序
- {
- int begin = left;
- int end = right;
- int pivot = begin;//记录坑位的下标
- int key = a[begin];//坑值
-
- while (begin < end)
- {
- //右边找小,放到左边
- while (begin < end && a[end] >= key)//与坑值比较
- {
- --end;
- }
- //小的放在左边的坑里,自己形成了新的坑位
- a[pivot] = a[end];
- pivot = end;
-
- //左边找大,放在右边
- while (begin < end && a[begin] <= key)
- {
- ++begin;
- }
- //大的放在右边的坑里,自己形成了新的坑位
- a[pivot] = a[begin];
- pivot = begin;
- }
- a[pivot] = key;
- return pivot;//返回坑位
- }
-
- //借助数据结构栈模拟递归过程
- void QuickSortNonR(int *a,int n)
- {
- Stack com;//定义Stack结构体类型变量
- STDataTYpe scope;//这个结构体类型的变量主要存储数据区间[left,right]。
-
- //初始化栈
- StackInit(&com);
-
- scope.left =0;
- scope.right= n - 1;
- //入栈(区间)
- StackPush(&com,scope);
-
- while (!StackEmpty(&com))//判断栈是否为空
- {
- //记录一下左右区间,不然区间结构的值会因为输出栈顶元素而改变
- int left = scope.left;
- int right = scope.right;
-
- scope = StackTop(&com);//输出栈顶元素
- StackPop(&com);//出栈
-
- //挖坑法单趟排
- int keyIndex = QuickSort(a, scope.left, scope.right);
-
- //分割区间
- //[left,keyIndex-1], keyIndex ,[keyIndex+1,right]
- //区间只有一个元素或区间不存在,不执行入栈scope
- //注意入栈顺序
- if (keyIndex + 1 < right)//区间只有一个元素或区间不存在,不执行入栈
- {
- scope.left = keyIndex + 1;
- scope.right = right;
-
- StackPush(&com, scope);//入栈
- }
-
- if (left < keyIndex-1)//后进先出
- {
- scope.left = left;
- scope.right = keyIndex - 1;
-
- StackPush(&com, scope);//入栈
- }
- }
- //释放空间
- StackDesTory(&com);//在堆区上开辟的空间,用完之后需要主动free释放。
- }
-
- //打印
- void Print(int* a, int n)
- {
- for (int i = 0; i < n; ++i)
- {
- printf("%d ", a[i]);
- }
- }
- int main()
- {
- int a[] = {49,38,65,97,76,13,27,49};
- //挖坑法
- QuickSortNonR(a,sizeof(a) / sizeof(a[0]));
- Print(a,sizeof(a) / sizeof(a[0]));
- return 0;
- }


三、归并非递归算法
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法 (Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序 列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
如果大家对归并排序的逻辑,递归的递归算法还不了解的朋友可以观看博主的另一篇博客。
常见排序算法之归并排序——归并排序_保护小周ღ的博客-CSDN博客
3.1 算法思想
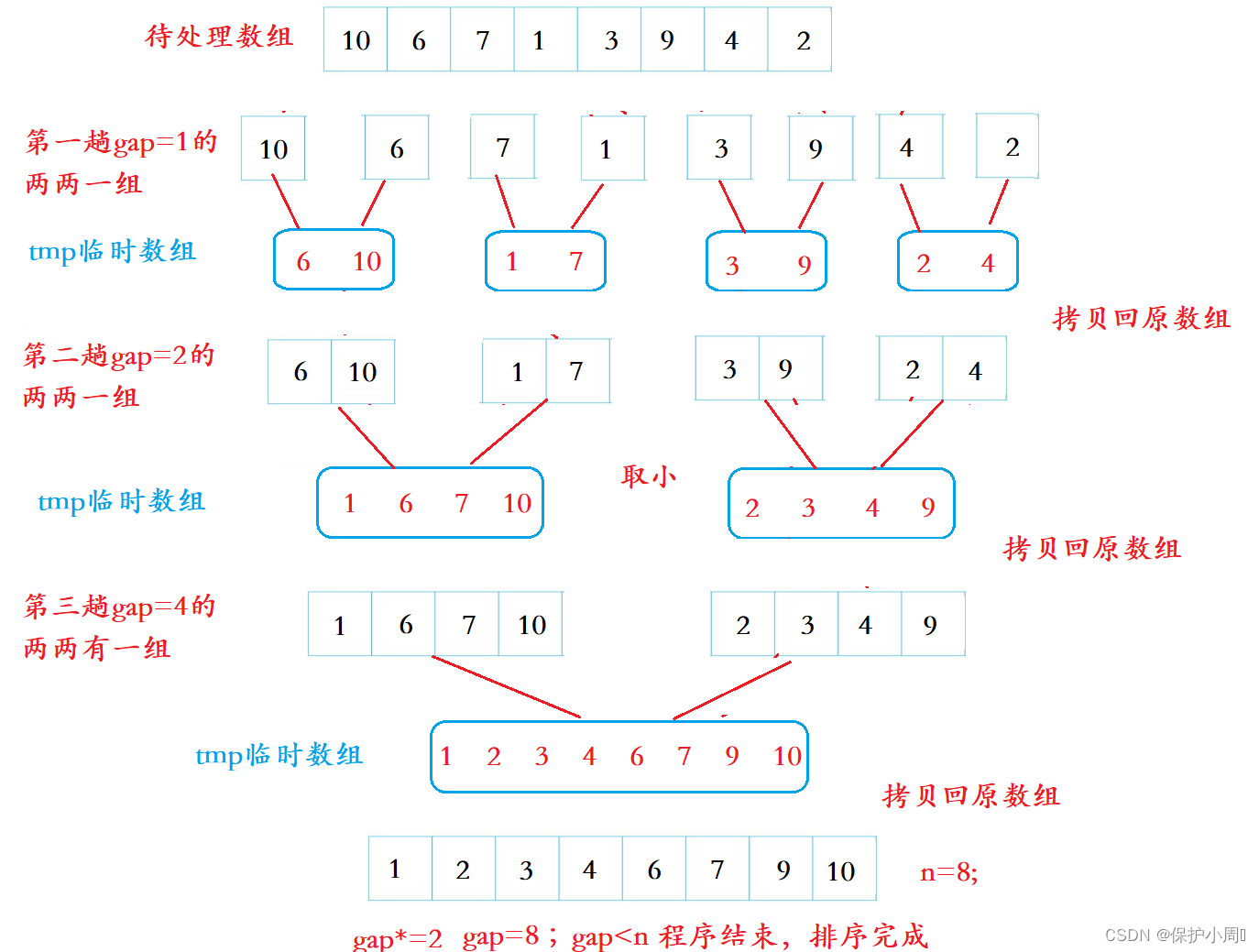
本次不使用栈模拟递归,而是用循环代替递归,首先通过循环控制gap来划分区间,然后子循环遍历每一个区间,每一个区间,执行归并操作(升序取小),主要难点是控制区间越界问题。
gap:每组数据个数,n为数组长度
(1)归并过程中右半区间可能不存在(程序会划分左右区间,右半区间的值>n-1越界),因为元素可能不是2的次方倍。
解决方法,break;中止循环,就不会执行归并操作,一个区间是不用归并的。
(2)归并过程中右半区间的值<gap(最后一个区间<gap),也会造成越界访问。
解决方法,重新划分边界值,避免越界,区间右值=n-1(n为数组长度);然后遍历区间执行归并就不会越界了。
3.2 程序实现
- #define _CRT_SECURE_NO_WARNINGS
-
- #include<stdio.h>
- #include<stdlib.h>//动态开辟空间的函数的头文件
-
- //打印
- void Print(int* a, int n)
- {
- for (int i=0;i<n;++i)
- {
- printf("%d ",a[i]);
- }
- }
-
- //归并非递归排序
- void MergeSortNonR(int *a,int n)
- {
- int* tmp = (int*)malloc(sizeof(int) * n);//动态开辟与待排序数组大小相等的一片连续的空间
-
- //gap=1是区间[0,0],[1,1],[2,2]……归并
- //gap=2是区间[0,1],[2,3],[4,5]……归并
- //gap=4是区间[0,3],[4,7],[8,11]……归并
- //……
- int gap = 1;//每组数据个数
- while (gap < n)
- {
- for (int i = 0; i < n; i += 2 * gap)//可以转到下一对区间
- {
- //[i,i+gap-1] ,[i+gap,i+2*gap-1]……
- //归并
- int begin1 = i, end1 = i+gap-1;
- int begin2 = i+gap, end2 = i + 2 * gap - 1;
-
- //归并过程中右半区间可能不存在,因为可能不是2的整数倍
- if (begin2 >n-1)
- break;//中止程序
-
- //归并过程中右半区间的值<gap,也会造成越界访问
- if (end2 >n-1)
- end2 = n - 1;//重新划分边界值,避免越界
-
- int index = i;
-
- while (begin1 <= end1 && begin2 <= end2)//有一个子序列遍历完,循环结束
- {
- if (a[begin1] < a[begin2])//升序,取小
- {
- tmp[index++] = a[begin1++];
-
- }
- else
- {
- tmp[index++] = a[begin2++];
- }
- }
-
- //判断子序列是否遍历完,未遍历完毕的子序列剩余元素直接给到tmp数组
- while (begin1 <= end1)
- {
- tmp[index++] = a[begin1++];
- }
-
- while (begin2 <= end2)
- {
- tmp[index++] = a[begin2++];
- }
- //拷贝回去
- for (int j = i; j <= end2; ++j)
- {
- a[j] = tmp[j];
- }
- }
- gap *= 2;
- }
- free(tmp);//释放动态开辟的空间
- }
- int main()
- {
- int a[] = {10,6,7,1,3,9,4,2};
- MergeSortNonR(a, sizeof(a) / sizeof(a[0]));
- //MergeSort(a,sizeof(a)/sizeof(a[0]));
- Print(a,sizeof(a)/sizeof(a[0]));
- return 0;
- }

3.3 拓展知识
归并排序也叫外排序,可以对文件中数据进行排,假设10G的数据放到硬盘的文件中,要排序,如何排,如果操作系统将这组数据调入内存中,可能内存不够。其他的排序自然而然就用不了,假设有1G的内存可用。10G的文件切分为10个1G的文件,并且让10个1G的文件有序。每次读一个1G的文件到内存,放到一个数组,用快排对其排序,再将有序数据写回文件,再继续读下一个文件。得到10个有序的1G文件,即可用递归排序,两两一组,合成一个新的有序文件。
关于文件的读写操作,感兴趣的同学可以订阅博主的专栏C语言,里面有文件的基本操作(上)(下),同时C技能树,文件的基本操作也收录了这两篇博客。
四、总结
非递归算法与递归算法相比起来性能上来将其实并没有很大的提升,递归对于现在的CPU性能来讲也是没有问题的,主要是怕极端情况下,就数据量特别多的时候,需要建立很深的栈帧,栈空间不够,如果使用数据结构的“栈”模拟递归,就不会出现这种情况(数据结构栈是在内存的堆区上建立的,而堆是用G做单位)。
至此快速排序、归并排序的非递归算法博主已经分享完了,相信大家对这个逻辑有了一定的理解,大家可以自己动手敲敲代码,感受一下。

本期收录于博主的专栏——排序算法,适用于编程初学者,感兴趣的朋友们可以订阅,查看其它“常见排序”。排序算法_保护小周ღ的博客-CSDN博客
感谢每一个观看本篇文章的朋友,更多精彩敬请期待:保护小周ღ *★,°*:.☆( ̄▽ ̄)/$:*.°★*
文章多处存在借鉴,如有侵权请联系修改删除!
五、栈(Stack)源代码
Stack.h
- #pragma once
-
- #include<stdio.h>
- #include<stdlib.h>
- #include<assert.h>
- #include<stdbool.h>
-
- //数据类型
- typedef struct STDataTYpe//区间
- {
- int left;
- int right;
- }STDataTYpe;//方便以后更改类型
-
-
- //栈的定义
- typedef struct Stack
- {
- STDataTYpe* data;
- int top;//栈顶,记录有多少数据
- int capacity;//记录动态数组的最大空间,增容
- }Stack;
-
-
- //初始化
- void StackInit(Stack*ps);
-
- //入栈
- void StackPush(Stack*ps,STDataTYpe x);
-
- //出栈
- void StackPop(Stack*ps);
-
- //输出栈顶
- STDataTYpe StackTop(Stack*ps);
-
- //输出栈数据个数
- int StackSize(Stack *ps);
-
- //判断栈是否为空
- bool StackEmpty(Stack* ps);
-
- //释放空间
- void StackDesTory(Stack* ps);

Stack.c
- #include"Stack.h"
-
- //初始化
- void StackInit(Stack* ps)
- {
- ps->data = (STDataTYpe*)malloc(sizeof(STDataTYpe)*4);
- if (ps->data== NULL)//判断是否申请成功
- {
- perror("malloc");
- exit(-1);
- }
- ps->capacity = 4;
- ps->top = 0;
- //区间初始化
- ps->data->left = 0;
- ps->data->right = 0;
- }
-
- //入栈
- void StackPush(Stack* ps, STDataTYpe scope)
- {
- assert(ps);
- //满了扩容
- if (ps->top==ps->capacity)
- {
- STDataTYpe* tmp = (STDataTYpe*)realloc(ps->data, ps->capacity * 2*sizeof(STDataTYpe));
- if (tmp == NULL)
- {
- perror("realloc");
- exit(-1);
- }
- else
- {
- ps->data = tmp;
- ps->capacity *= 2;
- }
- }
- //区间入栈
- ps->data[ps->top].right = scope.right;
- ps->data[ps->top].left = scope.left;
-
- ps->top++;
- }
-
- //出栈
- void StackPop(Stack* ps)
- {
- assert(ps);
- //栈空,调用Pop,直接中止元素
- assert(ps->top>=0);
- ps->top--;
- }
-
- //输出栈顶
- STDataTYpe StackTop(Stack* ps)
- {
- assert(ps);
- //栈空,调用Top,直接中止元素
- assert(ps->top >= 0);
- return ps->data[ps->top-1];
- }
-
- //输出栈数据个数
- int StackSize(Stack *ps)
- {
- assert(ps);
- return ps->top;
- }
-
- //判断栈是否为空
- bool StackEmpty(Stack* ps)
- {
- assert(ps);
-
- return ps->top == 0;
- }
-
- //释放空间
- void StackDesTory(Stack* ps)
- {
- assert(ps);
- free(ps->data);
- ps->data = NULL;
- ps->top = ps->capacity = 0;
- }





