一、PCA原理（原文讲的特别好）

PCA原理： https://blog.csdn.net/u012005313/article/details/50877366
(1)方差： 我们希望投影后投影值尽可能分散，而这种分散程度，可以用数学上的方差表述
(2)协方差：用两个字段的协方差表示其相关性。当协方差为0时，表示两个字段完全独立。为了让协方差为0，我们选择第二个基时只能在与第一个基正交的方向上选择。因此最终选择的两个方向一定是正交的。

降维问题的优化目标：将一组N维向量降维K维(k大于0，小于N)，其目标是选择K个单位(模为1)正交基，使得原始数据变换到这组基上后，各字段两两间协方差为0，而字段的方差则尽可能大（在正交的约束下，取最大的K个方差）。

(3) 协方差矩阵

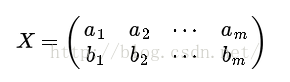
C是一个对称矩阵，其对角线分别是各个字段的方差，而第i行j列和j行i列元素相同，表示i和j两个字段的协方差

(4) 协方差矩阵对角化
要进行优化，等价于将协方差矩阵对角化：即除对角线外的其他元素化为0，并且在对角线上将元素按大小从上到下排列，这样我们就达到了优化目的

优化目标变成了寻找一个矩阵P，满足PCPT是一个对角矩阵，并且对角元素按从大到小依次排列，那么P的前K行就是要寻找的基，用P的前K行组成的矩阵乘以X就使得X从N维降到了K维并满足上述优化条件。

PCA本质上是将方差最大的方向作为主要特征，并且在各个正交方向上将数据“离相关”，也就是说让它们在不同正交方向上没有相关性（协方差）。

在人脸识别中，PCA是对测量空间中的数据，通过KL分解映射到维数较小的特征空间，这个特征空间成为特征脸空间。因此，该方法也叫做特征脸方法。

PCA是一种以较少数量的特征对样本进行描述以达到降低特征空间维数的方法，方法的基础是Karhunen-Loeve展开式，简称KL展开式。

得到降维的子空间，任何一幅人脸图像都可以向其投影并获得一组坐标系数，成为KL分解系数。这组系数表明了该图像在子空间中的位置，从而可以作为人脸识别的依据，这些系数也可以称为该图像的代数特征。因为C的特征向量量化后可以看出人脸的轮廓，所以又称为特征脸。

实际的人脸识别过程中，对于一个输入的测试样本x，求它与平均脸之间的偏差y = x - x’，则y在特征脸空间的投影可以表示为系数向量z = W(T)y，z就是KL变换的展开系数向量。(T)表示转置。