n皇后问题（DFS）_比赛 题库 提交记录 hack! 博客 帮助 好评差评[-5] #58. n皇后问题百度翻译实时翻

n皇后问题是指在一个n*n的国际象棋棋盘上放置n个皇后，使得这n个皇后两两均不在同一行、同一列、统一对角线上，求合法的方案数。

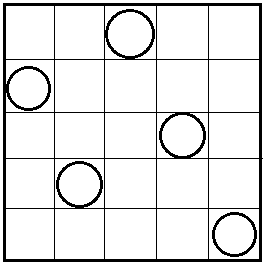
每两个皇后不在同一行也不在一列，同时也不在一个对角线上
判断不在同一对角线：
//第row行皇后的列号为temp[row]，第pre行皇后的列号为temp[pre]
if abs(row-pre) == abs(temp[row]-temp[pre]) ： 则冲突

使用DFS思想

1. 只求方案数，不需要求解出其中的过程那么我们就不需要进行回溯

python

n = int(input()) #皇后数量
temp = [0 for x in range(n)]   #暂存皇后
ans = 0 #方案数
def valid(temp,row,col): #验证皇后是否在同一列、同一对角线
    for pre in range(row):
        if (abs(row-pre) == abs(col-temp[pre])) or temp[pre]==col:
            return 0	#冲突
    return 1
def dfs(temp,row):
    global ans,n
    if row == n: #走到最后得到合法的方案
        ans += 1	#计算方案数+1
        return
    else:
        for col in range(n):
            if valid(temp,row,col) == 1: #col可以放皇后
                temp[row] = col
                dfs(temp,row+1)
dfs(temp,0)
print(ans)			
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

C++

#include<bits/stdc++.h>
using namespace std;
const int maxn = 10;
//n为皇后数量,temp暂存当前皇后的摆放位置,ans为方案数 
//hashTable为散列数组，标志x是否已经在temp中 
int n,temp[maxn],ans = <
1
2
3
4
5