剑指 Offer II 020. 回文子字符串的个数——马拉车Manacher算法

马拉车算法 Manacher‘s Algorithm 是用来查找一个字符串的最长回文子串的线性方法，由一个叫Manacher的人在1975年发明的，这个方法的最大贡献是在于将时间复杂度提升到了线性。

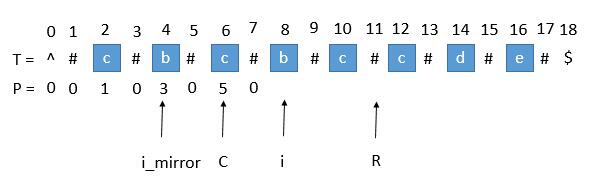
首先我们解决下奇数和偶数的问题，在每个字符间插入"#"，并且为了使得扩展的过程中，到边界后自动结束，在两端分别插入 “^” 和 “$”，两个不可能在字符串中出现的字符，这样中心扩展的时候，判断两端字符是否相等的时候，如果到了边界就一定会不相等，从而出了循环。经过处理，字符串的长度永远都是奇数了。

T数组是修改后的数组，P数组是标明回文长度的部分。只要P/2就能得到原始数组中回文长度的部分。

求每个 P [ i ]

接下来是算法的关键了，它充分利用了回文串的对称性。
我们用 C 表示回文串的中心，用 R 表示回文串的右边半径
。所以 R = C + P[ i ] 。C 和 R 所对应的回文串是当前循环中 R 最靠右的回文串。
让我们考虑求 P [ i ] 的时候，如下图。
用 i_mirror 表示当前需要求的第 i 个字符关于 C 对应的下标。
情况一、如果i不被R包括在内，在R外面。那么直接暴力求解，没有快捷的方法，从左从右计算即可。

情况二、如果i被R包括在内：

i_mirror是i关于C的对称，我们计算i_mirror的左侧对称是否在L的内部，如果在内部，那么P[i]=P[i_mirror]

如果不在内部，那么P[i]=(R-i)*2

如果恰好在边缘位置，也就是i_mirror与LR重叠，那么我们从R开始最近的字符开始验证。

代码：（只有res部分无关，别的都是manacher算法本身）

class Solution {
    public int countSubstrings(String s) {
                    if(s == null || s.length()==0 ) return 0;
            char[] str = s.toCharArray();
            char[] mstr = new char[str.length*2+1];
            int[] p = new int[mstr.length]; //放置回文半径的数组
            int index = 0;
            int res = 0;
            mstr[0] = '#';
            for(int i=1;i< mstr.length;i++){
                mstr[i] = str[index++];
                mstr[i+1] = '#';
                i++;
            }
            int C = -1; //中心位置
            int R = -1; //R代表的是终止 注意R不算
            for(int i=0;i<mstr.length;i++){
                //对每个位置求回文
                p[i] = R > i ? Math.min(p[2*C-i],R-i) : 1;
                //如果R不大于i 也就是i在R外 至少第一个位置不用验证 都是#
                //如果R大于i 也就是i在R内 至少那些位置不用验证？
                //就是R到i的距离作为回文半径 与 p[2*C-i]也就是i_mirror的回文半径 最小的那个
                //就不用验证了
                // e # a # [b] # a [C] # a # [b] # a # e # [R]
                //比如这种情况 最小值 b 的回文半径为 1（不考虑#） 而R到b的距离为2
                //我们只需要考虑b的回文半径

                while(i + p[i] < mstr.length && i - p[i] > -1){
                    //意思是：直接看能不能直接往外验证
                    //这个while的判断条件就是不越界
                    //已经找到了最近不需要扩验的
                    if(mstr[i+p[i]]==mstr[i-p[i]]){
                        p[i]++;
                    } else {
                        break;
                    }
                    //注意这个if 就是开始向外验证 但是根据我们的分析 如果碰到其他情况会直接break
                    //如果进了if了 就说明到了回文半径的边界了 进入2.3的情况
                }

                if(i+p[i]>R){
                    R = i+p[i];
                    C = i;
                }//更新R和C
                //这时候p数组里面就是回文半径了
                res = res+p[i]/2;
            }
            return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50