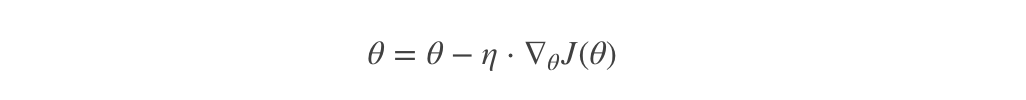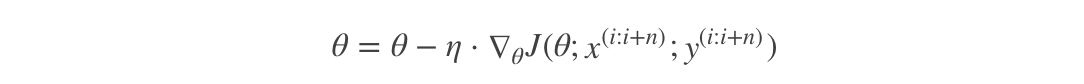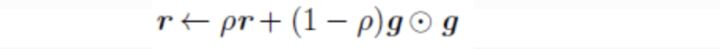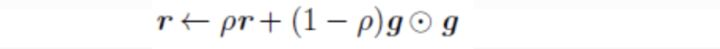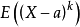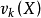pytorch优化器知识总结整理_梯度更新时,是更新一个批次的还是整个的

引用链接：
https://www.jianshu.com/p/39dac1e24709
https://zhuanlan.zhihu.com/p/78622301
https://blog.csdn.net/qq_41855990/article/details/107405837

FGD（Full gradient descent）全梯度下降法

计算训练集所有样本误差，对其求和再取平均值作为目标函数。
权重向量沿其梯度相反的方向移动，从而使当前目标函数减少得最多。
因为在执行每次更新时，我们需要在整个数据集上计算所有的梯度，所以批梯度下降法的速度会很慢，同时，批梯度下降法无法处理超出内存容量限制的数据集。
批梯度下降法同样也不能在线更新模型，即在运行的过程中，不能增加新的样本。
其是在整个训练数据集上计算损失函数关于参数θ的梯度：

SGD（stochastic gradient descent）

看来，SGD每次只是取出一个样本来计算更新梯度，并不是像全梯度下降算法似的，一次性计算全部样本的梯度，然后更新。其每轮计算的目标函数不再是全体样本误差，而仅是单个样本误差，即每次只代入计算一个样本目标函数的梯度来更新权重，再取下一个样本重复此过程，直到损失函数值停止下降或损失函数值小于某个可以容忍的阈值。
算法评价
优点:
虽然SGD需要走很多步的样子，但是对梯度的要求很低（计算梯度快）。而对于引入噪声，大量的理论和实践工作证明，只要噪声不是特别大，SGD都能很好地收敛。应用大型数据集时，训练速度很快。比如每次从百万数据样本中，取几百个数据点，算一个SGD梯度，更新一下模型参数。相比于标准梯度下降法的遍历全部样本，每输入一个样本更新一次参数，要快得多。
缺点:
SGD在随机选择梯度的同时会引入噪声，使得权值更新的方向不一定正确。此外，SGD也没能单独克服局部最优解的问题。
torch.optim.SGD(params,lr=,momentum=0,dampening=0,weight_decay=0,nesterov=False)
参数：
–params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
–lr (float) – 学习率
–momentum (float, 可选) – 动量因子（默认：0，通常设置为0.9，0.8）
–weight_decay (float, 可选) – 权重衰减（L2惩罚）（默认：0）
–dampening (float, 可选) – 动量的抑制因子（默认：0）
–nesterov (bool, 可选) – 使用Nesterov动量（默认：False）论文：http://www.cs.toronto.edu/~hinton/absps/momentum.pdf
例子：
optimizer = torch.optim.SGD(model.parameters(), lr=0.1, momentum=0.9)
optimizer.zero_grad()
loss_fn(model(input), target).backward()
optimizer.step()

推荐程度：不推荐！

使用动量(Momentum)的随机梯度下降法(SGD)

使用动量(Momentum)的随机梯度下降法(SGD)，主要思想是引入一个积攒历史梯度信息动量来加速SGD。更新的时候在一定程度上保留之前更新的方向，用法为在torch.optim.SGD的momentum参数不为零。
优点：加快收敛速度，有一定摆脱局部最优的能力，一定程度上缓解了没有动量的时候的问题。
缺点：仍然继承了一部分SGD的缺点

上述公式在吴恩达的深度学习课程中就是指数加权平均，公式稍有不同。不过β取0.9（相当于上面公式γ取0.9）是公认的好取值

优化算法寻找目标函数最小值的过程就像使用一个小球在一个超平面滚来滚去最终滚到最低点的过程。SGD每次通过一个批次的数据决定小球接下来要滚的方向，由于每次只使用一个小批次的数据计算梯度，得到的梯度只是损失函数在这一小批次数据上的梯度。所以各个批次数据得到的梯度有一定的方差，小球每次滚的方向和距离都不一样。但是大致方向上小球还是朝着最低点前进的。如图（a）所示。
带Momentum的SGD在训练时仿佛有惯性一样，会沿着前面一段时间的梯度方向往前“冲”，就像本身具有“动量”一样。这也是Momentum名字的由来。每当小球要转变方向时，例如从“向右上”转到“向右下”，由于“动量”的存在，之前一段时间“向上”方向的动量和当前时刻“向下”方向的动量抵消，之前一段时间“向右”的动量和现在时刻“向右”的动量叠加，所以小球可以少走弯路，更快的滚向最低点。动量可以在方向错误时将其“拉”回来，方向正确时将其再“推”快点。如图（b）所示。
再举个例子：

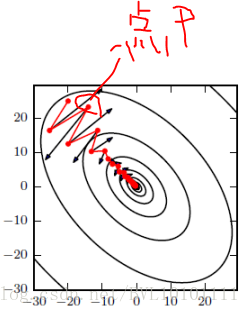
如图所示，红色为SGD+Momentum。黑色为SGD。可以看到黑色为典型Hessian矩阵病态的情况，相当于大幅度的徘徊着向最低点前进。而由于动量积攒了历史的梯度，如点P前一刻的梯度与当前的梯度方向几乎相反。因此原本在P点原本要大幅徘徊的梯度，主要受到前一时刻的影响，而导致在当前时刻的梯度幅度减小。
直观上讲就是，要是当前时刻的梯度与历史时刻梯度方向相似，这种趋势在当前时刻则会加强；要是不同，则当前时刻的梯度方向减弱。
可以看出，区别于普通的SGD就是增加了过去的趋势。

推荐程度：可以一试

使用牛顿加速度（NAG, Nesterov accelerated gradient）的随机梯度下降法（SGD）

可以理解为往标准动量中添加了一个校正因子
理解策略：在Momentun中小球会盲目地跟从下坡的梯度，容易发生错误。所以需要一个更聪明的小球，能提前知道它要去哪里，还要知道走到坡底的时候速度慢下来而不是又冲上另一个坡。

上面那个折线图我没看懂，但是其理论非常妙啊~！
优点：梯度下降方向更加准确
缺点：对收敛率的作用却不是很大

推荐程度：不如不试（此话引自https://www.jianshu.com/p/39dac1e24709，但从算法介绍看上去比**使用动量(Momentum)的随机梯度下降法(SGD)**要好一点，毕竟这是对于它的改进算法）

小批量梯度下降算法（mini-batch）

小批量梯度下降算法是FGD和SGD的折中方案,在一定程度上兼顾了以上两种方法的优点。
每次从训练样本集上随机抽取一个小样本集，在抽出来的小样本集上采用FGD迭代更新权重。
被抽出的小样本集所含样本点的个数称为batch_size，通常设置为2的幂次方，更有利于GPU加速处理。
特别的，若batch_size=1，则变成了SGD；若batch_size=n，则变成了FGD.其迭代形式为

SAGD（随机平均梯度下降(Stochastic Averaged Gradient Descent)）

在SGD方法中，虽然避开了运算成本大的问题，但对于大数据训练而言，SGD效果常不尽如人意，因为每一轮梯度更新都完全与上一轮的数据和梯度无关。
随机平均梯度算法克服了这个问题，在内存中为每一个样本都维护一个旧的梯度，随机选择第i个样本来更新此样本的梯度，其他样本的梯度保持不变，然后求得所有梯度的平均值，进而更新了参数。
如此，每一轮更新仅需计算一个样本的梯度，计算成本等同于SGD，但收敛速度快得多。

小结

全梯度下降算法（FGD）【知道】
在进行计算的时候,计算所有样本的误差平均值,作为我的目标函数
随机梯度下降算法（SGD）【知道】
每次只选择一个样本进行考核
小批量梯度下降算法（mini-batch）【知道】
选择一部分样本进行考核
随机平均梯度下降算法（SAG）【知道】
会给每个样本都维持一个平均值,后期计算的时候,参考这个平均值

AdaGrad

class torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0)
参数：
–params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
–lr (float, 可选) – 学习率（默认: 1e-2）
–lr_decay (float, 可选) – 学习率衰减（默认: 0）
–weight_decay (float, 可选) – 权重衰减（L2惩罚）（默认: 0）
优点：它可以自动调节学习率，不需要人为调节
缺点：仍依赖于人工设置一个全局学习率，随着迭代次数增多，学习率会越来越小，最终会趋近于0

确实利于稀疏数据，稀疏数据0比较多，这样的话直接就会使得某些参数的梯度为0，使得这些类的参数分母较小，从而学习率较大，更新的幅度越大。不过我感觉这样的更新策略也未必总是对的吧，仅仅根据出现频率来决定学习率不知道是否有理论依据，具体论文我也没看，不知是否有强有力的理论支撑。但是它的缺点是十分明显的，越训练到后面，学习率几乎为0。

推荐程度：不推荐

Rprop

1、首先为各权重变化赋一个初始值，设定权重变化加速因子与减速因子。
2、在网络前馈迭代中当连续误差梯度符号不变时，采用加速策略，加快训练速度；当连续误差梯度符号变化时，采用减速策略，以期稳定收敛。
3、网络结合当前误差梯度符号与变化步长实现BP，同时，为了避免网络学习发生振荡或下溢，算法要求设定权重变化的上下限。
torch.optim.Rprop(params, lr=0.01, etas=(0.5, 1.2), step_sizes=(1e-06, 50))
参数
–params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
–lr (float, 可选) – 学习率（默认：1e-2）
–etas (Tuple[float,float], 可选) – 一对（etaminus，etaplis）, 它们分别是乘法的增加和减小的因子（默认：0.5，1.2）
–step_sizes (Tuple[float,float], 可选) – 允许的一对最小和最大的步长（默认：1e-6，50）
不同权值参数的梯度的数量级可能相差很大，因此很难找到一个全局的学习步长。
靠参数梯度的符号，动态的调节学习步长
适用于full-batch learning，不适用于mini-batch learning，为什么呢？设想现在有一个十步的mini-batch，结果前九次梯度都是+0.1，结果最后一次梯度是-0.9，那么最好的且应该采取的做法就是，梯度相互抵消，几乎不变，而然Rprop会增加9次梯度，减去1次梯度，从而达到某个极端的数值，从而导致该算法无法应用于mini-batch情况，只能全量训练。这一重大缺点导致该算法几乎没人会用。。

RMSProp

RMSProp其实是对于AdaGrad的改进。

RMSprop是Geoff Hinton提出的一种自适应学习率方法。Adagrad会累加之前所有的梯度平方，而RMSprop仅仅是计算对应的平均值，因此可缓解Adagrad算法学习率接近为0的弊端。
首先给出AdaGrad算法：

再抛出原始的RMSProp算法:

可以看出RMSProp优化算法和AdaGrad算法唯一的不同，就在于累积平方梯度的求法不同。RMSProp算法不是像AdaGrad算法那样暴力直接的累加平方梯度，而是加了一个衰减系数来控制历史信息的获取多少。见下：


直观理解作用
简单来讲，设置全局学习率之后，每次通过，全局学习率逐参数的除以经过衰减系数控制的历史梯度平方和的平方根，使得每个参数的学习率不同。
那么它起到的作用是什么呢？
起到的效果是在参数空间更为平缓的方向，会取得更大的进步（因为平缓，所以历史梯度平方和较小，对应学习下降的幅度较小），并且能够使得陡峭的方向变得平缓，从而加快训练速度。
下面通过例子讲解一下：
假设我们现在采用的优化算法是最普通的梯度下降法mini-batch。它的移动方向如下面蓝色所示：

假设我们现在就只有两个参数w,b，我们从图中可以看到在b方向走的比较陡峭，这影响了优化速度。
而我们采取AdaGrad算法之后，我们在算法中使用了累积平方梯度：

从上图可以看出在b方向上的梯度g要大于在w方向上的梯度。
那么在下次计算更新的时候，r是作为分母出现的，越大的反而更新越小，越小的值反而更新越大，那么后面的更新则会像下面绿色线更新一样，明显就会好于蓝色更新曲线。

在参数空间更为平缓的方向，会取得更大的进步（因为平缓，所以历史梯度平方和较小，对应学习下降的幅度较小），并且能够使得陡峭的方向变得平缓，从而加快训练速度。
这就是RMSProp优化算法的直观好处。

Adam

1.Adam算法可以看做是修正后的Momentum+RMSProp算法
2.动量直接并入梯度一阶矩估计中（指数加权）
3.Adam通常被认为对超参数的选择相当鲁棒
4.学习率建议为0.001
再看算法：其实就是Momentum+RMSProp的结合，然后再修正其偏差。

我们可以看到图中多出了一步叫做偏差修正操作，那个是指数加权平均法中的基本操作，具体可以参见博客：https://blog.csdn.net/qq_41076797/article/details/110768164
另外我想介绍一下关于矩的知识，在数理统计学中有一类数字特征称为矩。
原点矩：令k为正整数（或为0），a为任何实数，X为随机变量，则期望值
叫做随机变量X对a的k阶矩，或叫动差。如果a=0，则有E（X^k），叫做k阶原点矩，记作
，也叫k阶矩。
优点：
1、对目标函数没有平稳要求，即loss function可以随着时间变化
2、参数的更新不受梯度的伸缩变换影响
3、更新步长和梯度大小无关，只和alpha、beta_1、beta_2有关系。并且由它们决定步长的理论上限
4、更新的步长能够被限制在大致的范围内（初始学习率）
5、能较好的处理噪音样本，能天然地实现步长退火过程（自动调整学习率）
6、很适合应用于大规模的数据及参数的场景、不稳定目标函数、梯度稀疏或梯度存在很大噪声的问题

推荐程度：非常推荐，基本上是最最常用的优化方法

如有不妥，请联系我！