SLAM代码（三维重建）_三角测量法获得射影重建代码

三维重建的一般步骤
- 特征点对计算基础矩阵。
- 根据基础矩阵计算相机矩阵
- 对于内个点对计算点在3D空间的位置。
The Fundamental Matrix Song

本文主要介绍三维重建的初始值的估计方法（三角测量triangulation）
这样看来三维重建综合了几个问题（包括上述三角测量，以及其他的问题包括基础矩阵估计，），如下图所示

采用光束平差法对射影空间下的多个相机运动矩阵及目标的三维结构进行优化。光束平差法一般在各种重建算法的最后一步使用。这种优化方法的最大特点是可以处理数据丢失情况并提供真正的最大似然估计。但同时，其要求提供一个好的初始值，即首先确定射影空间下的相机运动矩阵和三维结构。采用三角测量法确定目标的射影空间的三维坐标可以得到好的初始值。具体步骤见图2。

其中需要介绍一些基础知识

分层重建

• Projective reconstruction
• Affine reconstruction
• Metric reconstruction

如果从图像能获得在景物平面的某个仿射坐标系下的二维射影变换$H$,则这个变换的逆$H^{-1}$ 作用到图像点 m 就可以得到它所对应的景物点在景物平面的仿射坐标系下的坐标 $X = H^{−1}m$ ,从而可以得到平面景物的仿射结构。类似地,如果从图像能获得在景物平面的欧氏坐标系下的二维射影变换$H$,如果这个欧氏坐标系的度量单位与绝对 ( 或实际 ) 度量相差一个常数倍,则可以通过景物的图像点和变换$H$可以得到景物的相似结构;如果这个欧氏坐标系的度量单位与绝对度量相等,则通过景物的图像点和变换$H$可以得到景物的绝对欧氏结构。因此,恢复平面景物的仿射结构,等价于某个仿射坐标系下确定景物平面到图像平面的射影变换;恢复平面景物的度量结构,等价于在某个欧氏坐标系下确定景物平面到图像平面的射影变换;恢复平面景物的绝对欧氏结构,等价于在某个绝对欧氏坐标系下确定景物平面到图像平面的射影变换。

欧式重建的中已知绝对二次曲线即可恢复欧式几何的全部信息。

三角测量

三角原理的重构结果,是否为空间景物的欧氏结构取决于摄像机所处的世界坐标系。也就是说,如果世界坐标系是欧氏的,则重构结果是空间景物的欧氏结构;否则如果世界坐标系是仿射的(或射影的) ,则重构结果是空间景物的仿射结构(或射影结构) 。
在计算目标相对无人机的位置关系中，使用三角测量方法可以获得相对相机坐标系下目标的三维位置。具体原理如下。

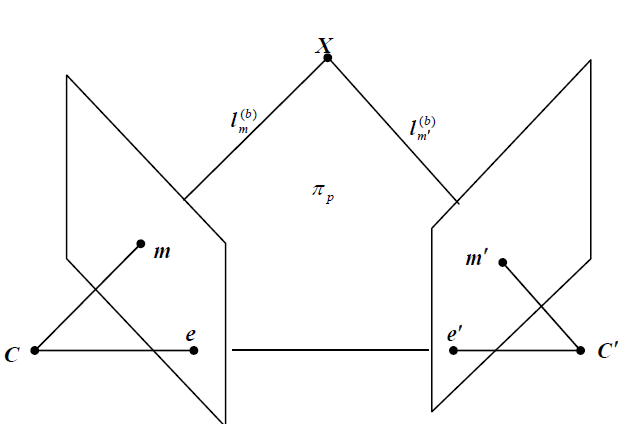
相机在2个对应的位姿下得到个视图的图像。两幅图像在同一世界坐标系下的摄像机矩阵P 和P′，m ↔ m′是两幅图像的一个点对应，即它们满足极几何约束${m}{{'}^{T}}Fm = 0$，现在要根据P和P′计算点对应m↔ m′的空间点X。m的反投射线 ${m}^{\left( b \right)}$ 与m′的反投射线 $l_{{m}'}^{\left( b \right)}$确定了通过两摄像机光心的一张平面