- 1欢迎参加SPDK线上中文讨论会议
- 2阿里开源高性能搜索引擎 Havenask - Ha3
- 3Windows10多显卡修改默认高性能卡_windows server 更改默认显卡
- 4Python爬虫常用哪些库?_python爬虫库
- 5FPGA编程语言--VHDL OR Verilog?_fpga语言
- 6机器人仿真论文阅读1_机器人仿真设计论文
- 7yolov8 多卡训练报错subprocess.CalledProcessError: Command‘[‘/home/... returned non-zero exit status 1._yolov8多卡训练报错
- 8JAVA 中 Switch引用Enum问题
- 9Spark内核架构剖析_spark sql内核剖析 下载
- 10js中的map和set_js map赋值set
数据机构之二叉树_1234567依次构造平衡二叉树
赞
踩
二叉树
一、二叉树的定义和分类
1、二叉树的定义
二叉树是一种特定的树,每个结点最多有两棵子树,并且左右子树不能交换位置。
这意味着下面几棵树是完全不同的树。

2、几种特殊的二叉树
满二叉树
高度为h并且结点数为2^h-1的树为满二叉树,即每个层都有最大结点数。
因此满二叉树的叶子结点都在最底下一层。并且若按层按顺序为结点编号对于结点i,如果有双亲,必为(向下取整)(i/2),如果有孩子,左孩子必为2 * i, 右孩子必为2 * i + 1。
完全二叉树
高度为h有n个结点的二叉树,当且仅当其每一个结点都与高度为h的满二叉树中编号一一对应时的二叉树为满二叉树。
完全二叉树的性质:
- 若i<=(向下取整)(i/2)则结点i为分支否则i为叶子结点;
- 叶子结点只能在最大的两层出现;
- 度为1的结点只可能有一个,且该结点只有左孩子没有右孩子;

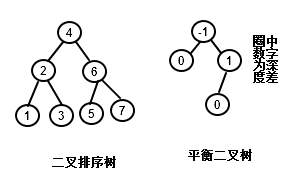
二叉排序树
左子树上的所有结点的关键字小于根结点的关键字;右子树上的所有结点均大于根结点的关键字的二叉树为二叉排序树
二叉平衡树
任意结点的左右子树的深度只差不超过一的二叉树为二叉平衡树。
3、二叉树的性质
- 非空二叉树的叶子结点等于度为2的结点树加1
- 非空二叉树第h层最多有2^(h-1)个结点;
- 高度为h的二叉树最多有2^h-1个结点;
- 具有n个结点的完全二叉树的高度为(向上取整)(log_2(N+1))或(向下取整)(log_2N + 1)。
4、二叉树的基本操作
- InitBiTree(&T) 初始化二叉树
- DestroyBiTree(&T) 销毁二叉树
- CreateBiTree(&T, definiton) 按照definition的定义构造二叉树
- ClearBiTree(&T) 清空二叉树
- BiTreeEmpty(T) 二叉树判空
- BiTreeDepth(T) 二叉树的深度
- Value(e) 返回e的数据
- Assign(&e, value) 将e的数据赋值为value
- Root(T) 返回二叉树的根结点
- Parent(T) 返回非根结点的双亲
- LeftChild(e) 返回e的左孩子
- RightChild(e) 返回e的右孩子
- LeftSibling(T, e) 返回e的左兄弟
- RightSibling(T, e) 返回e的右兄弟
- PreTraverse(T, visit()) 前序遍历
- InTraverse(T, visit()) 中序遍历
- PostTraverse(T, visit()) 后序遍历
- LevelTraverse(T, visit()) 层序遍历
二、二叉树的存储结构
1、顺序存储
二叉树的顺序存储是利用完全二叉树的性质进行存储。假如有一颗普通的二叉树,然后将不存在的结点补满构成完全二叉树再按顺序存储,因为元素的相对位置一定固定,因此很容易定位。但是对空间的浪费很多,因为有大量不是树中的元素被存储。

2、链式存储
因为顺序存储二叉树对空间的利用率较低因此二叉树采用链式存储的较多,链式存储是维护两个分别指向左右孩子的指针和一个数据域的结构。

二叉树的链式存储描述
typedef struct BiNode
{
ElemType data; //数据域
struct BiNode* lchild, rchild; //左右孩子指针
}BiNode,* BiTree;
- 1
- 2
- 3
- 4
- 5
三、二叉树的相关操作
参考树:
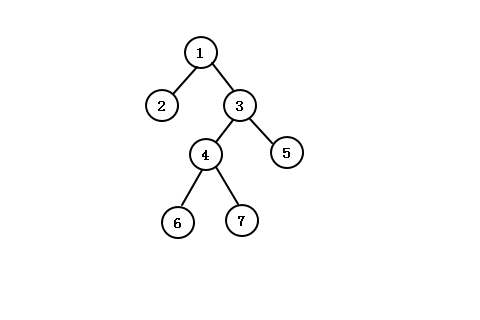
1、先序遍历
先访问根结点,然后先序遍历左子树,再先序遍历右子树。
上述树先序遍历后的结果是:1234675
递归实现代码:
typedef void (*visit)(ElemType)
void PreTraverse(BiTree T, visit func)
{
if(T != NULL)
{
func(T); //遍历根结点
PreTraverse(T->lchild, func); //遍历左子树
PreTraverse(T->rchild, func); //遍历右子树
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
2、中序遍历
中序遍历左子树,然后访问根结点,再中序遍历右子树。
上述树中序遍历后的结果是:2164735
递归实现代码:
typedef void (*visit)(ElemType);
void InTraverse(BiTree T, visit func)
{
if(T != NULL)
{
InTraverse(T->lchild, func); //遍历左子树
func(T);
InTraverse(T->rchild, func); //遍历右子树
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
3、后序遍历
后序遍历左子树,然后后序遍历右子树,再访问根结点。
上述树的后序遍历的结果为:2674531
递归实现代码:
typedef void (*visit)(ElemType);
void PostTraverse(BiTree T, visit func)
{
if(T != NULL)
{
PostTraverse(T->lchild, func);
PostTraverse(T->rchild, func);
func(T)
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
4、非递归实现中序遍历
树的非递归实现是利用栈的FILO特性实现的,对于任一结点P
- 若其左孩子不为空,则将P入栈并将P的左孩子置为当前的P,然后对当前结点P再进行相同的处理;
- 若其左孩子为空,则取栈顶元素并进行出栈操作,访问该栈顶结点,然后将当前的P置为栈顶结点的右孩子;
- 直到P为NULL并且栈为空则遍历结束。
非递归实现代码:
typedef void (*visit)(ElemType); void InTraverseWithStack(BiTree T, visit func) { sqStack S; InitStack(&S); BiTree p = T; while(p || isEmpty(S)) { if(p) { push(&S, p); p = p->lchild; } else { pop(&S, &p); func(p); p = p->rchild; } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
5、层次遍历
层次遍历是指一层一层的遍历二叉树,上述树的层序遍历是1234567
先将树的根节点入队,如果队列不空,则进入循环
将队首元素出队,并输出它;
如果该队首元素有左孩子,则将其左孩子入队;
如果该队首元素有右孩子,则将其右孩子入队。
实现代码:
typedef void (*visit)(ElemType); void LevelTraverse(BiTree T, visit func) { sqQueue Q; InitQueue(&Q); BiTree p; EnQueue(&Q, T); while(!IsEmptyQUeue(Q)) { DeQueue(&Q, &p); func(p); if(p->lchild != NULL) { EnQueue(&Q, &p->lchild); } if(p->rchild != NULL) { EnQueue(&Q, &p->rchild); } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
四、特殊二叉树的具体定义和相关操作
1、线索二叉树及其操作
线索二叉树的定义和结构
因为二叉树中一定存在叶子结点,就意味着一定存在指针未被利用。而且n个结点的二叉树悬空指针一定是n+1个。因此我们需要利用起这些悬空指针。规定若结点无左子树,则左子树的指针指向其前驱结点,若无右子树则指向其后继结点。(这里的前驱后继是按照遍历之后的结果得出的比如先序遍历为12345则2的前驱为1后继为3,不同遍历结果前驱和后继不同)
结构定义

typedef int ElemType;
typedef struct ThreadNode
{
ElemType data;
struct ThreadNode* lchild, rchild;
int ltag, rtag;
}ThreadNode,* ThreadTree;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
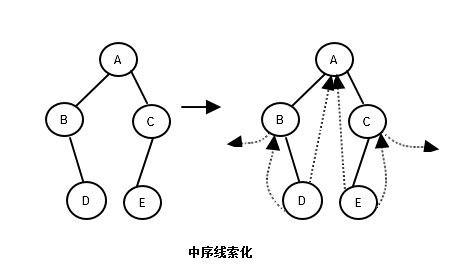
二叉树的线索化
二叉树的线索化实际上是遍历一次二叉树对二叉树的中结点的空指针进行修改。
- 1
实现代码:
- 1
void InThread(ThreadTree* p, ThreadNode* pre) { if((*p) != NULL) { InThread((*p)->lchild, pre); if((*p)->lchild == NULL) { (*p)->lchild = pre; (*p)->ltag = 1; } if(pre != NULL && pre->rchild == NULL) { pre->rchild = (*p); pre->rtag = 1; } pre = (*p); InThread(&p->rchild, pre); }//if }//InThread void CreateInThread(ThreadTree* T) { ThreadTree pre = NULL; if((*T) != NULL) { InThread(T, pre); pre->lchild = NULL; pre->rtag = 1; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
线索二叉树的遍历
1)、求中序遍历的第一个结点
ThreadNode* FirstNode(ThreadTree T)
{
while(T->ltag == 0)
{
p = p->lchild;
}
return p;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
2)、求该结点中序遍历中的后继结点
ThreadNode* NextNode(ThreadNode* p)
{
if(p->rtag == 0)
{
return FirstNode(p->rchild);
}
return p->rchild;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
3)、中序遍历
typedef void (*visit)(ElemType data)
void ThreadInTraverse(TreadTree T,visit func)
{
for(ThreadNode* p = FirstNode(T); p != NULL; p = NextNode(p))
{
func(p->data);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
2、二叉排序树
二叉排序树的查找
之前说过二叉排序树的结构很简单就是左子树上的所有结点的关键字小于根结点的关键字;右子树上的所有结点均大于根结点的关键字的二叉树。那么查找起来也很方便。
非递归实现:
BSTNode* BSTFind(BSTree T,ElemType cur) { BSTNode* p = NULL; while(T != NUL && cur != T->data) { p = T; if(cur < T->data) { T = T->lchild; } else { T = T->rchild; } } return T; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
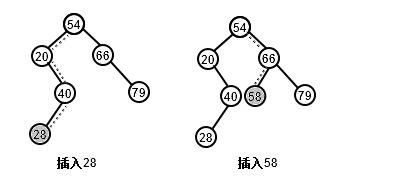
二叉排序树的插入
二叉排序树的插入有点类似于查找:
若二叉树为空则直接插入结点,否则若关键字小于根结点的关键字则插入到左子树中,若关键字大于根结点的关键字则插入到右子树中。
int BSTInsert(BiTree* T, ElemType cur) { if((*T) == NULL) { (*T) = (BiTree)malloc(sizeof(BINode)); (*T)->data = cur; (*T)->lchild = (*T)->rchild = NULL; retutn TRUE; //successfully } if(k == (*T)->data) { return FALSE; //failurely } if(cur < (*T)->data) { return BSTInsert(&(*T)->lchild, cur); } if(cur > (*T)->data) { return BSTInsert(&(*T)->rchild, cur); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
二叉排序树的删除
二叉排序树的删除要求删除后的二叉树必须还是二叉排序树。
删除过程:
- 如果被删除的结点是叶子结点就直接删除;
- 如果被删除的结点只有一颗左子树或者右子树则用该结点的孩子代替该结点,再删除;
- 如果该结点有两棵子树则该结点的直接后继或者直接前驱代替该结点然后从树中删除代替该结点的结点。

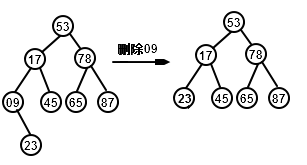
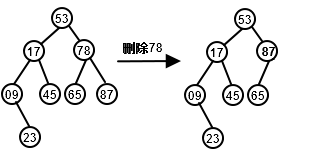
注意
二叉排序树的平均查找长度为O(log_2n)但是平衡二叉树并不唯一因此查找效率还和二叉树本身有关。比如
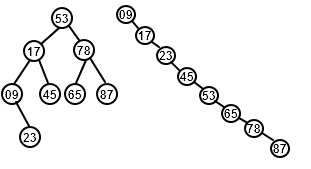
上面两种情况都是同一列数据的二叉排序树,但是明显右边的不如左边的查找效率高,因此二叉排序树的结构对其查找效率影响很大。
2、平衡二叉树的相关操作
前面提到过平衡二叉树是任意结点的左右子树的深度只差不超过一的二叉树。,同样在删除和插入元素之后必须保持其特性。在平衡二叉树中当插入和删除结点导致的平衡树的不平衡问题都可以都是在最小不平衡子树上进行的,最小不平衡子树是插入或删除路径上离插入结点最近的平衡因子的绝对值大于1的结点最为根的子树。
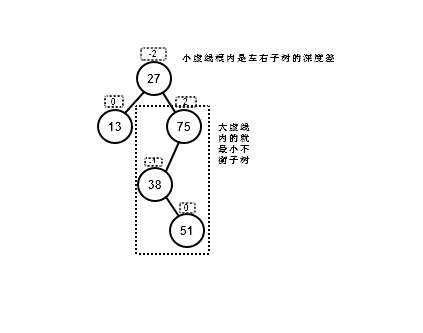
当插入一个元素导致平衡树不平衡则用一下方法进行调整:
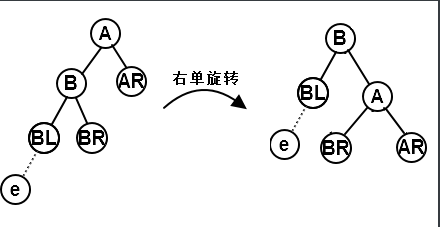
LL平衡旋转(右单旋转)
当在结点的左孩子的左子树上插入元素导致平衡被破坏时就进行一次向右的旋转操作。如图所示,将A的左孩子B向右上旋转代替A成为根结点,将A结点向下右下旋转成为B的右子树的根结点,而B的原右子树则作为A结点的左子树。(e为将要插入的元素)
RR平衡旋转(左单旋转)
当在结点的右孩子的右子树上插入元素时导致平衡被破坏时就进行一次向左的旋转操作。如图所示,将A的右孩子B向左上旋转代替A成为根结点,将A结点向左下旋转成为B的左子树的根结点,而B的原左子树则作为A结点的右子树。

LR平衡旋转(先左后右旋转)
当在结点的左孩子的右子树上插入结点导致平衡被破坏时先左旋转后右旋转。先将A结点的左孩子的右子树的根结点C向左上旋转提升到B结点的位置,然后将C结点向右上旋转提升到A结点的位置。

RL平衡旋转(先右后左旋转)
当在结点的右孩子的左子树上插入结点导致平衡被破坏时先右旋转后左旋转。先将A的右孩子的左子树的根结点C向右上旋转提升到B结点的位置,然后再把该C结点向左上旋转提升到A结点的位置。

删除时处理相同,可以将删除后造成的不平衡看作插入造成的不平衡。
2、哈夫曼树
有一些树为树中结点赋予一个特定意义的数值称为权,而权存储在结点的数据域,从树倒任意路径的长度与该结点上的权值的乘积称为结点的带权路径长度。而树的带权路径长度是所有结点的带权路径长度之和。比如下面的树,结点上的数值就是对应结点的权,并且只有叶子结点有权。

该树的带权路径长为WPL=4×2+12×3+3×7=65。
而哈夫曼树就是相同的权重不同的组合方式中WPL最小的树也称为最优二叉树。
霍夫曼树的构造
- 将N个结点分别作为N棵二叉树,构成一个森林;
- 从森林中寻找带权路径长最小的两棵构成新的树;
- 删除上一步选中的两颗树,将新生成的树插入到森林;
- 重复2,3两步直到只剩一颗树为止。
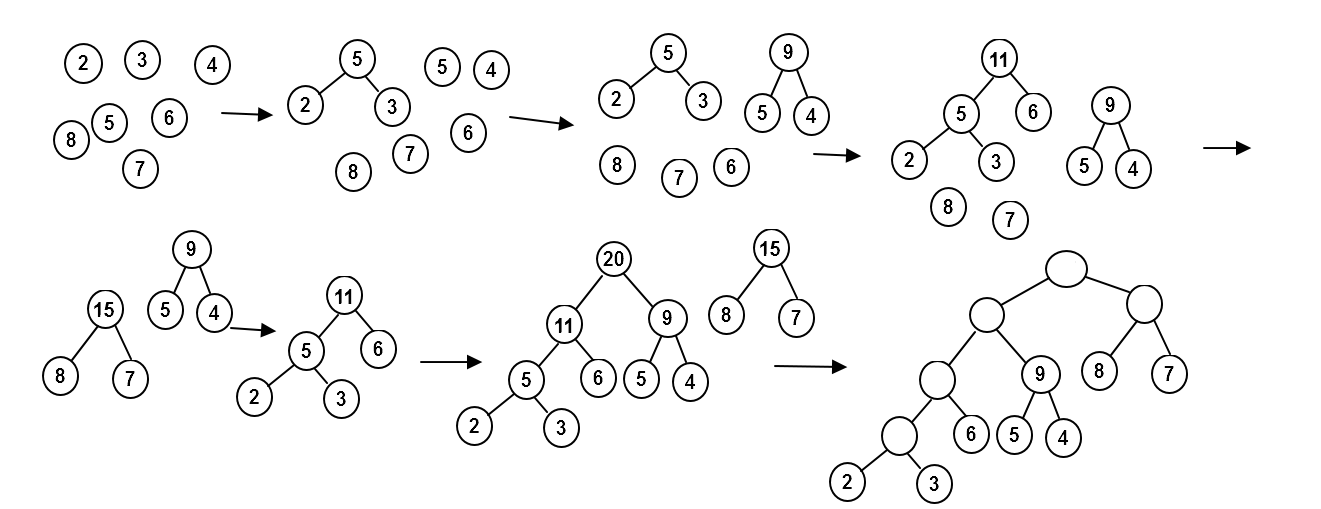
最终的WPL=35



