devbox
很楠不爱3
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

数据结构 - 树及二叉树的应用_数据结构 二叉树的应用

作者：很楠不爱3 | 2024-06-14 14:53:26

赞

踩

数据结构 二叉树的应用

目录

1. 数组, 链表, 树存储方式分析

1.1 数组存储方式分析

1.2 链表存储方式分析

1.3 树存储方式分析

 2. 树示意图及常用术语

3. 二叉树概述

4. 二叉树图示

5. 二叉树遍历

5.1 说明

5.2 应用实例 

5.2.1 思维图解

5.2.2 要求

6. 二叉树查找

6.1 要求

6.2 思维分析示例图

7. 二叉树删除

7.1 要求

7.2 思路分析图解

8. 核心代码实现

8.1 节点类核心代码

8.2 二叉树类核心代码

1. 数组, 链表, 树存储方式分析

1.1 数组存储方式分析

        优点：通过下标方式访问元素，速度快。对于有序数组，还可使用二分查找提高检索速度。

        缺点：如果要检索具体某个值，或者插入值(按一定顺序)会整体移动，效率较低。

        操作示意图：

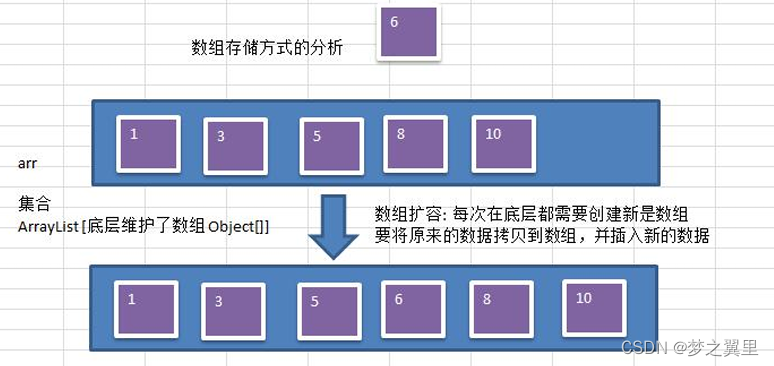
1.2 链表存储方式分析

        优点：在一定程度上对数组存储方式有优化(比如：插入一个数值节点，只需要将插入节点，链接到链表中即可， 删除效率也很好)。

        缺点：在进行检索时，效率仍然较低，比如(检索某个值，需要从头节点开始遍历)。

        操作示意图：

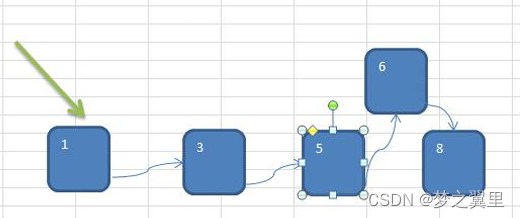
1.3 树存储方式分析

        能提高数据存储，读取的效率, 比如利用 二叉排序树(Binary Sort Tree)，既可以保证数据的检索速度，同时也可以保证数据的插入，删除，修改的速度。

        案例: [7, 3, 10, 1, 5, 9, 12]

        操作示意图：

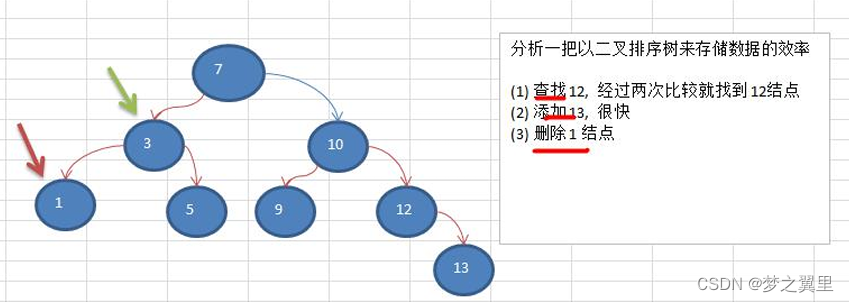
 2. 树示意图及常用术语

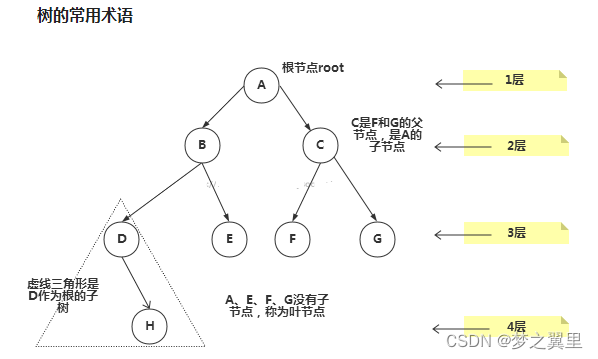
3. 二叉树概述

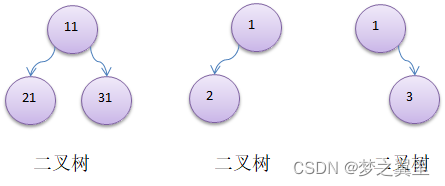
  1. 树有很多种，每个节点最多只能有两个子节点的一种形式称为二叉树。

  2. 二叉树的子节点分为左节点和右节点。

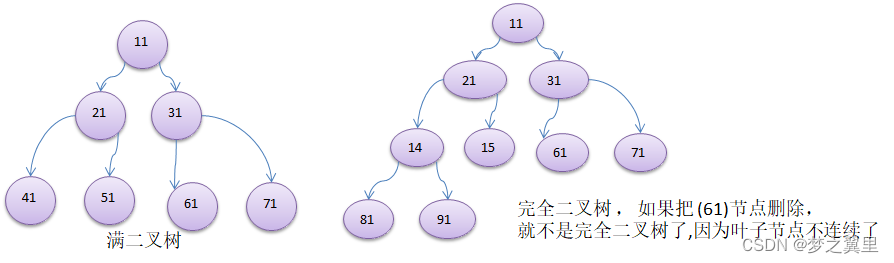
  3. 如果该二叉树的所有叶子节点都在最后一层，并且结点总数= 2^n -1 , n 为层数，则我们称为满二叉树。

  4. 如果该二叉树的所有叶子节点都在最后一层或者倒数第二层，而且最后一层的叶子节点在左边连续，倒数第二层的叶子节点在右边连续，我们称为完全二叉树。

4. 二叉树图示

5. 二叉树遍历

5.1 说明

  1. 使用前序，中序和后序对下面的二叉树进行遍历。

  2. 前序遍历: 先输出父节点，再遍历左子树和右子树【父 - 左 - 右】

  3. 中序遍历: 先遍历左子树，再输出父节点，再遍历右子树【左 - 父 - 右】

  4. 后序遍历: 先遍历左子树，再遍历右子树，最后输出父节点【左 - 右 - 父】

  5. 小结: 看输出父节点的顺序，就确定是前序，中序还是后序

5.2 应用实例 
5.2.1 思维图解

5.2.2 要求

  1. 前上图的 3号节点 "卢俊" , 增加一个左子节点 [5, 关胜]

  2. 使用前序，中序，后序遍历，请写出各自输出的顺序是什么

6. 二叉树查找

6.1 要求

  1. 请编写前序查找，中序查找和后序查找的方法。

  2. 并分别使用三种查找方式，查找 heroNO = 5 的节点

  3. 并分析各种查找方式，分别比较了多少次

6.2 思维分析示例图

7. 二叉树删除

7.1 要求

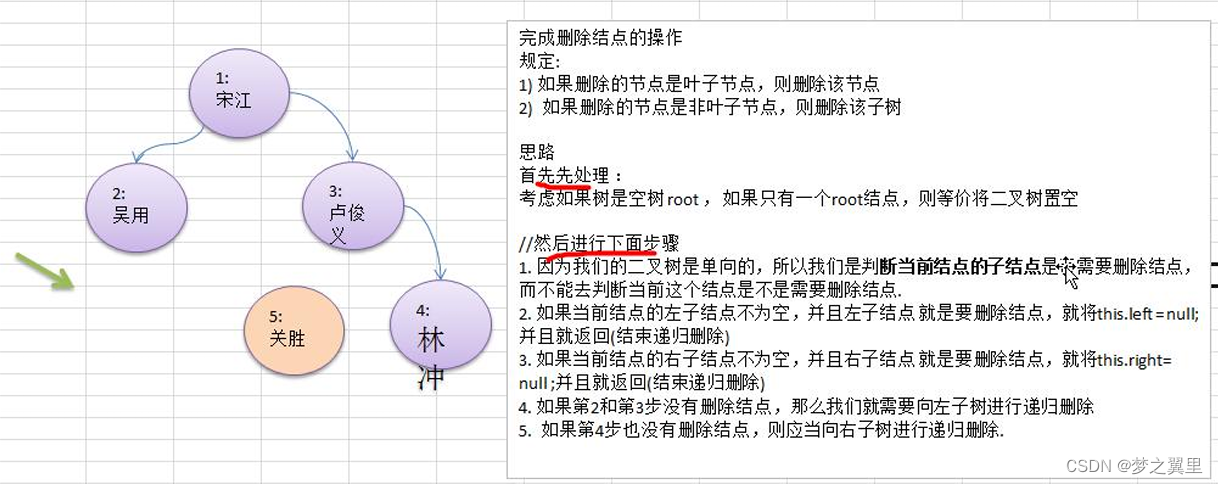
  1. 如果删除的节点是叶子节点，则删除该节点。

  2. 如果删除的节点是非叶子节点，则删除该子树。

  3. 测试，删除掉 5号叶子节点 和 3号子树。

7.2 思路分析图解

8. 核心代码实现

8.1 节点类核心代码
  1. // 前序遍历
  2. public void preOrder() {
  3. 	// 输出当前节点
  4. 	System.out.print(this + " ");
  5. 	// 如果左节点不为空
  6. 	if (Optional.ofNullable(this.getLeft()).isPresent()) {
  7. 		this.getLeft().preOrder();
  8. 	}
  9. 	// 如果右节点不为空
  10. 	if (Optional.ofNullable(this.getRight()).isPresent()) {
  11. 		this.getRight().preOrder();
  12. 	}
  13. }
  14. // 中序遍历
  15. public void infixOrder() {
  16. 	// 如果左节点不为空
  17. 	if (Optional.ofNullable(this.getLeft()).isPresent()) {
  18. 		this.getLeft().infixOrder();
  19. 	}
  20. 	// 输出当前节点
  21. 	System.out.print(this + " ");
  22. 	// 如果右节点不为空
  23. 	if (Optional.ofNullable(this.getRight()).isPresent()) {
  24. 		this.getRight().infixOrder();
  25. 	}
  26. }
  27. // 后序遍历
  28. public void afterOrder() {
  29. 	// 如果左节点不为空
  30. 	if (Optional.ofNullable(this.getLeft()).isPresent()) {
  31. 		this.getLeft().afterOrder();
  32. 	}
  33. 	// 如果右节点不为空
  34. 	if (Optional.ofNullable(this.getRight()).isPresent()) {
  35. 		this.getRight().afterOrder();
  36. 	}
  37. 	// 输出当前节点
  38. 	System.out.print(this + " ");
  39. }
  40. /**
  41. *
  42. * @Description 前序遍历查找
  43. * @param no 查找的编号
  44. * @return com.hui.data.struct.binaryTree.HeroNode
  45. */
  46. public HeroNode preOrderSearch(int no) {
  47.     System.out.println("前序遍历执行了~~~");
  48.     if (no == this.getId()) {
  49.        return this;
  50.     }
  51.     HeroNode curNode = null;
  52.     if (Optional.ofNullable(this.left).isPresent()) {
  53.        curNode = this.getLeft().preOrderSearch(no);
  54.     }
  55.     // 判断左子树是否存在查找的节点编号
  56.     if (Optional.ofNullable(curNode).isPresent()) {
  57.        return curNode;
  58.     }
  59.     if (Optional.ofNullable(this.right).isPresent()) {
  60.        curNode = this.getRight().preOrderSearch(no);
  61.     }
  62.     return curNode;
  63. }
  64. /**
  65.  *
  66.  * @Description 中序遍历查找
  67.  * @param no 查找的编号
  68.  * @return com.hui.data.struct.binaryTree.HeroNode
  69.  */
  70. public HeroNode infixOrderSearch(int no) {
  71.     HeroNode curNode = null;
  72.     if (Optional.ofNullable(this.left).isPresent()) {
  73.        curNode = this.getLeft().infixOrderSearch(no);
  74.     }
  75.     // 判断左子树是否存在查找的节点编号
  76.     if (Optional.ofNullable(curNode).isPresent()) {
  77.        return curNode;
  78.     }
  79.     System.out.println("中序遍历执行了~~~");
  80.     if (no == this.getId()) {
  81.        return this;
  82.     }
  83.     if (Optional.ofNullable(this.right).isPresent()) {
  84.        curNode =  this.getRight().infixOrderSearch(no);
  85.     }
  86.     return curNode;
  87. }
  88. /**
  89.  *
  90.  * @Description 后序遍历查找
  91.  * @param no 查找的编号
  92.  * @return com.hui.data.struct.binaryTree.HeroNode
  93.  */
  94. public HeroNode postOrderSearch(int no) {
  95.     HeroNode curNode = null;
  96.     if (Optional.ofNullable(this.left).isPresent()) {
  97.        curNode =  this.getLeft().postOrderSearch(no);
  98.     }
  99.     // 判断左子树是否存在查找的节点编号
  100.     if (Optional.ofNullable(curNode).isPresent()) {
  101.        return curNode;
  102.     }
  103.     if (Optional.ofNullable(this.right).isPresent()) {
  104.        curNode =  this.getRight().postOrderSearch(no);
  105.     }
  106.     // 判断右子树是否存在查找的节点编号
  107.     if (Optional.ofNullable(curNode).isPresent()) {
  108.        return curNode;
  109.     }
  110.     System.out.println("后序遍历执行了~~~");
  111.     if (no == this.getId()) {
  112.        return this;
  113.     }
  114.     return null;
  115. }
  116. /**
  117. *
  118. * @Description 删除节点
  119. * @param no 要删除节点的编号
  120. */
  121. public void delNode(int no) {
  122.     // 验证当前节点的左结点是否为空并且是否等于删除节点的编号, 是则将该左结点至 null
  123.     if (Optional.ofNullable(this.getLeft()).isPresent() && this.getLeft().getId() == no) {
  124.        this.setLeft(null);
  125.        return;
  126.     }
  127.     // 验证当前节点的右结点是否为空并且是否等于删除节点的编号, 是则将该右结点至 null
  128.     if (Optional.ofNullable(this.getRight()).isPresent() && this.getRight().getId() == no) {
  129.        this.setRight(null);
  130.        return;
  131.     }
  132.     // 左子树递归删除
  133.     if (Optional.ofNullable(this.getLeft()).isPresent()) {
  134.        this.getLeft().delNode(no);
  135.     }
  136.     // 右子树递归删除
  137.     if (Optional.ofNullable(this.getRight()).isPresent()) {
  138.        this.getRight().delNode(no);
  139.     }
  140. }
8.2 二叉树类核心代码
  1. // 前序遍历
  2. public void preOrder() {
  3. 	if (Optional.ofNullable(root).isPresent()) {
  4. 		root.preOrder();
  5. 	} else {
  6. 		System.out.println("二叉树为空, 不可遍历!!!");
  7. 	}
  8. }
  9. // 中序遍历
  10. public void infixOrder() {
  11. 	if (Optional.ofNullable(root).isPresent()) {
  12. 		root.infixOrder();
  13. 	} else {
  14. 		System.out.println("二叉树为空, 不可遍历!!!");
  15. 	}
  16. }
  17. // 后序遍历
  18. public void postOrder() {
  19. 	if (Optional.ofNullable(root).isPresent()) {
  20. 		root.afterOrder();
  21. 	} else {
  22. 		System.out.println("二叉树为空, 不可遍历!!!");
  23. 	}
  24. }
  25. // 前序遍历查找
  26. public HeroNode preOrderSearch(int no) {
  27.     if (Optional.ofNullable(root).isPresent()) {
  28.        return root.preOrderSearch(no);
  29.     }
  30.     return null;
  31. }
  32. // 中序遍历查找
  33. public HeroNode infixOrderSearch(int no) {
  34.     if (Optional.ofNullable(root).isPresent()) {
  35.        return root.infixOrderSearch(no);
  36.     }
  37.     return null;
  38. }
  39. // 后序遍历查找
  40. public HeroNode postOrderSearch(int no) {
  41.     if (Optional.ofNullable(root).isPresent()) {
  42.        return root.postOrderSearch(no);
  43.     }
  44.     return null;
  45. }
  46. /**
  47.  *
  48.  * @Description 删除节点
  49.  * @param no 要删除节点的编号
  50.  */
  51. public void delNode(int no) {
  52.     if (Optional.ofNullable(root).isPresent()) {
  53.        if (root.getId() == no) {
  54.            root = null;
  55.        } else {
  56.            root.delNode(no);
  57.        }
  58.     } else {
  59.        System.out.println("是空树, 不能删除!!!");
  60.     }
  61. }

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/很楠不爱3/article/detail/718385
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号