很楠不爱3

这个屌丝很懒，什么也没留下！

热门标签

01背包问题_01背包问题 csdn

作者：很楠不爱3 | 2024-03-29 01:46:24

踩

01背包问题 csdn

定义

背包问题是动态规划的经典问题之一。根据物品限制条件的不同，背包问题可分为01背包、完全背包、多重背包、分组背包和混合背包（前4种背包的混合）等。

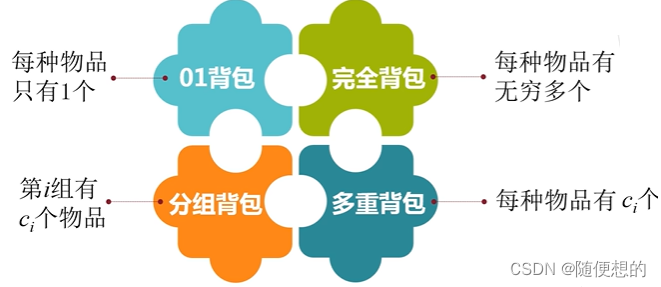
一、01背包

求解

（1）确定状态：c[i][j]表示前i种物品放入容量为j的背包中获得的最大价值。

（2）划分状态：第i阶段处理第i种物品，第i-1阶段处理第i-1种物品。当处理第i种物品时，前i-1种物品已处理完毕，只需考虑第i-1阶段向第i阶段的转移。

（3）决策选择。若背包容量不足，则不能放入，价值仍为前i-1种物品处理后的结果；若背包容量充足，则考察放入、不放入哪种情况获得的价值更大。

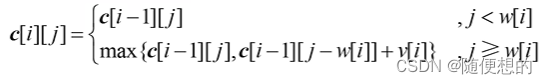
误认为容量够时，放入比不放入价值更大，但注意放入会导致j-w[i]，容量变了

（4）边界条件。c[0][j]=0，c[i][0]=0（物品数量和容量为0，价值都为0）

举例


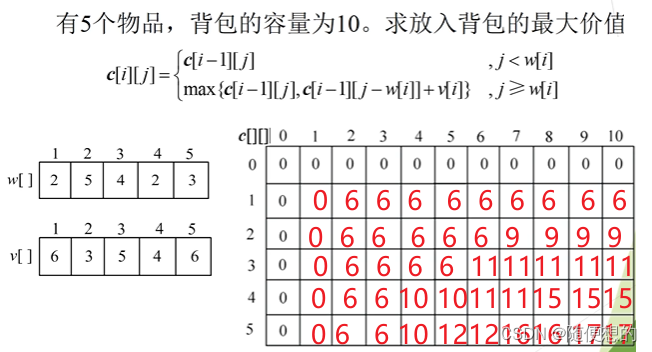
for(int i=1;i<=n;i++){
    for(int j=1;j<=W;j++){
        if(j<w[i])
            c[i][j]=c[i-1][j];
        else
            c[i][j]=max(c[i-1][j],c[i-1][j-w[i]]+v[i]);
    }
}

拓展延伸

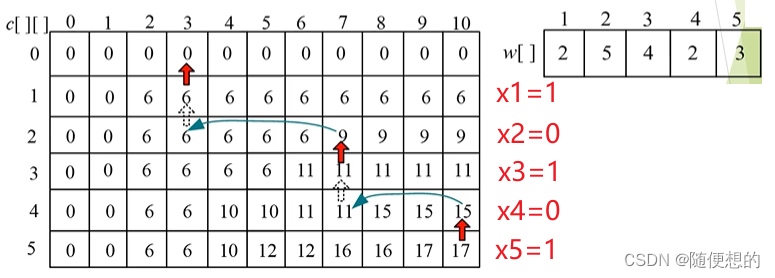
得到最大价值（最优值）后，还想知道具体放入了哪些物品。

①从右下角开始（i=n，j=W）

②若c[i][j]>c[i-1][j]，则第i个物品放进去了，x[i]=1（标记放了），j=j-w[i]

若c[i][j]<=c[i-1]，则第i个物品没放进去，x[i]=0（标记没放）。

③i--，转向第2步，直到i=0

算法优化

求解第i行时，只需要第i-1行的结果，前面的结果已经没用了；而求解c[i][j]时，只需要上一行j列或上一行j-w[i]列的结果。我们可以进行空间优化。

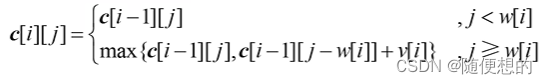
斐波那契：fn=fn-1+fn-2，fn-2=fn-1,fn-1=fn

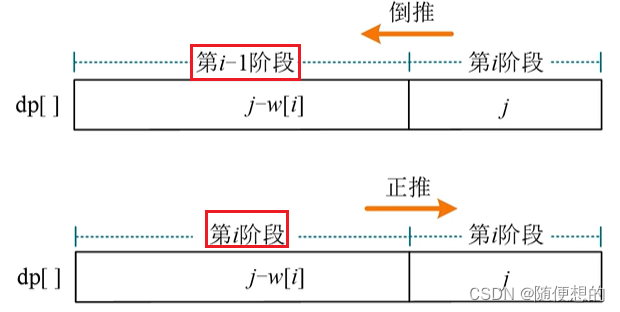
求解第i行，只需一个一维数组倒推即可。

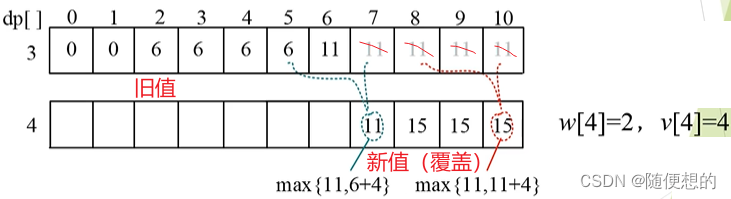
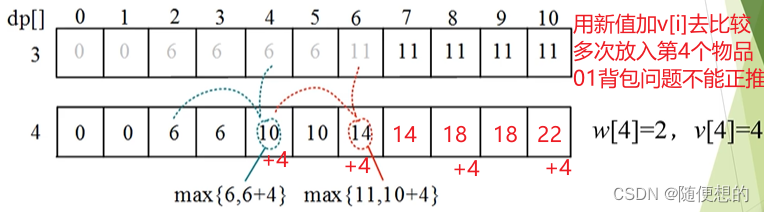
为什么不正推？


for(int i=1;i<=n;i++){
    for(int j=W;j>=w[i];j--){
        dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
    }
}

练习题

Bone Collector

知道是01背包后就简单了


#include<iostream>
#include<cstdio>
#include <cstring>
#define ll long long
#define INF 0x3f3f3f3f
using namespace std;
const int N=1000;
int n,v;
ll value[N+1],volume[N+1],dp[N+1];
 
void solve(){
    for(int i=1;i<=n;i++){
        for(int j=v;j>=volume[i];j--){
            dp[j]=max(dp[j],dp[j-volume[i]]+value[i]);
        }
    }
    printf("%d\n",dp[v]);
}
 
int main()
{
    int t;
    scanf("%d",&t);
    for (int i = 1; i <= t; i++){
        scanf("%d",&n);
        scanf("%d",&v);
        for(int j=1;j<=n;j++)
            scanf("%d",&value[j]);
        for(int j=1;j<=n;j++)
            scanf("%d",&volume[j]);
        memset(dp,0,sizeof(dp));//注意清0
        solve();
    }
    return 0;
}

二、完全背包

物品数量没有限制：每种物品有无限个，可以多次放入。采用正推形式求解。


for(int i=1;i<=n;i++){
    for(int j=w[i];j<=W;j++){
        dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
    }
}

练习题

Piggy-Bank

从题中可知，硬币的数量是无限的，所以这道题是完全背包问题，但这里求的最小价值，且需要准确达到质量，不能小于质量。前面的完全背包问题中，我们求最大值时并不要求刚好装满。

所以我们需要将代码进行变形。

①memset(dp,INF,sizeof(dp)); dp[0]=0；

最小值需要设为∞，若为0，0就是最小的。

②dp[j]=min(dp[j],dp[j-weight[i]]+value[i])

假设只有一个硬币价值30，质量50，dp[50]=30,dp[51]=∞，可以满足准确达到质量的要求。


#include<iostream>
#include<cstdio>
#include <cstring>
#define ll long long
#define INF 0x3f3f3f3f
using namespace std;
const int N=500;
const int M=10000;
int e,f,n;
int value[N+1],weight[N+1];
int dp[M+1];//dp[j] 表示重量为 j 的钱罐的最小花费
 
void solve(){
    dp[0]=0;//重量为 0 的钱罐不需要花费,没有硬币重量不为零时是无解的
    for(int i=1;i<=n;i++){
        for(int j=weight[i];j<=(f-e);j++){
            dp[j]=min(dp[j],dp[j-weight[i]]+value[i]);
        }
    }
    if(dp[f-e]==INF)printf("This is impossible.\n");
    else printf("The minimum amount of money in the piggy-bank is %d.\n",dp[f-e]);
}
 
int main()
{
    int t;
    scanf("%d",&t);
    for(int i=0;i<t;i++){
        scanf("%d",&e);
        scanf("%d",&f);
        scanf("%d",&n);
        for(int i=1;i<=n;i++){
            scanf("%d",&value[i]);
            scanf("%d",&weight[i]);
        }
        memset(dp,INF,sizeof(dp));//将所有元素初始化为无穷大（表示无解）
        solve();
    }
 
    return 0;
}

三、分组背包

有组物品，每一组选一个物品或不选（类似于01背包，选或不选）,使得背包内的物品价值总和最大。

用01背包思路来考虑，c[i][j]表示前i组物品放入容量为j的背包中获得的最大价值。

v[i][k]和w[i][k]分别表示第i组物品中第k个物品的价值和重量。

$c[i][j]=\left\{\begin{matrix} c[i-1][j] & ,j<w[i][k]\\ max(c[i-1][j],c[i-w[i][k]]+v[i][k])&, j>=w[i][k] \end{matrix}\right.$

和01背包一样，分组背包也能空间优化，不考虑前面的元素。


for(int i=1;i<=n;i++){
    for(int j=W;j>=1;j--){//遍历背包容量
        for(int k=1;k<=W;k++){//不同的背包容量，遍历第i组物品，选一个或不选第i组内的物品
            if(j>=w[i][k])
                dp[j]=max(dp[j],dp[j-w[i][k]+v[i][k]);
        }
    }
}

若第二层循环和第三层循互换。第i组第k个物品，遍历所有的背包容量，可能会使得第i组多个物品被放入背包中。

练习题

ACboy needs your help


#include<iostream>
#include<cstdio>
#include <cstring>
#define ll long long
#define INF 0x3f3f3f3f
using namespace std;
const int N=100;
int n,m;
int value[N+1][N+1],dp[N+1];
 
void solve(){
    for(int i=1;i<=n;i++){
        for(int j=m;j>=1;j--){
            for(int k=1;k<=m;k++){
                if(j>=k) 
                    dp[j]=max(dp[j],dp[j-k]+value[i][k]);
            }
        }
    }
    printf("%d\n",dp[m]);
}
 
int main()
{
    while(cin>>n>>m&&n&&m){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                scanf("%d",&value[i][j]);
            }
        }
        memset(dp,0,sizeof(dp));
        solve();
    }
    return 0;
}

四、多重背包

物品数量是有限个，第i种物品有ci个。可以通过暴力拆分或二进制拆分将多重背包问题转化为01背包问题，也可以通过数组优化解决可行性问题。

暴力拆分

暴力拆分指将第i中物品看作ci种独立的物品，每种物品只有一个，转化为01背包问题。


for(int i=1;i<=n;i++)
    for(int k=1;k<=c[i];k++)//多一层循环
        for(int j=W;j>=w[i];j--)
            dp[j]=max(dp[j],dp[j-w[i]]+v[i]);

二进制拆分

将c[i]个物品拆分成若干种新物品。存在一个最大的整数p，使 $2^{0}+2^{1}+2^{2}+...+2^{p}\leq c[i]$ ，剩余部分用 $R_i{}$ 表示，这可以将c[i]拆分为p+2个数： $2^{0},2^{1},2^{2},...,2^{p},R_i{}^{}$ 。

举例：假设有9个苹果，可以将这些苹果分成（1）、（1+1）、（1+1+1+1）、（1+1）四组，打包后得到4个不同的苹果：1、2、4、2，转换成了01背包。

$2^{p+1}-1\leq C_i{}\Rightarrow 2^{p+1}\leq C_i{}+1\Rightarrow p+1\leq log(C_i{}+1)\Rightarrow p+2\leq log(C_i{}+1)+1$


for(int i=1;i<=n;i++){
    if(c[i]*w[i]>=W){//相当于数量无限，可转化完全背包
        for(int j=w[i];i<=W;j++)
            dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
    }
    else{
        for(int k=1;c[i]>0;k<<=1){
            int x=min(k,c[i]);//如果k小，目前的物品是k*w[i],如果c[i]小，目前的物品是Ri*w[i]
            for(int j=W;j>=x*w[i];j--)
                dp[j]=max(dp[j],dp[j-x*w[i]]+x*v[i]);
            c[i]-=x;
        }
    }
    
 
}

数组优化

若不要求最优值，仅关注可行性（如面值是否能拼成）可用数组优化。用一个数组来记录使用了多少个第i种物品。


memset(dp,false,sizeof(dp));//dp[j]表示前i种硬币是否可以拼成价格j
int ans=0;//记录拼出的价格个数
dp[0]=true;
for(int i=1;i<=n;i++){//遍历每种硬币
    memset(num,0,sizeof(num));//num[j]表示拼成价格j时用了多少个第i种硬币
    for(int j=v[i];j<=W;j++){//遍历价格范围，从硬币的面值 v[i] 开始，到目标价格 W 结束
        if(!dp[j]&&dp[j-v[i]]&&num[j-v[i]]<c[i]){//当前价格 j 没有被拼出过,能够使用前 i 种硬币拼出价格为 j - v[i],拼出价格为 j - v[i] 时使用的第 i 种硬币数量小于其限制数量 c[i]
            dp[j]=true;
            num[j]=num[j-v[i]]+1;
            ans++;
        }
    }
}

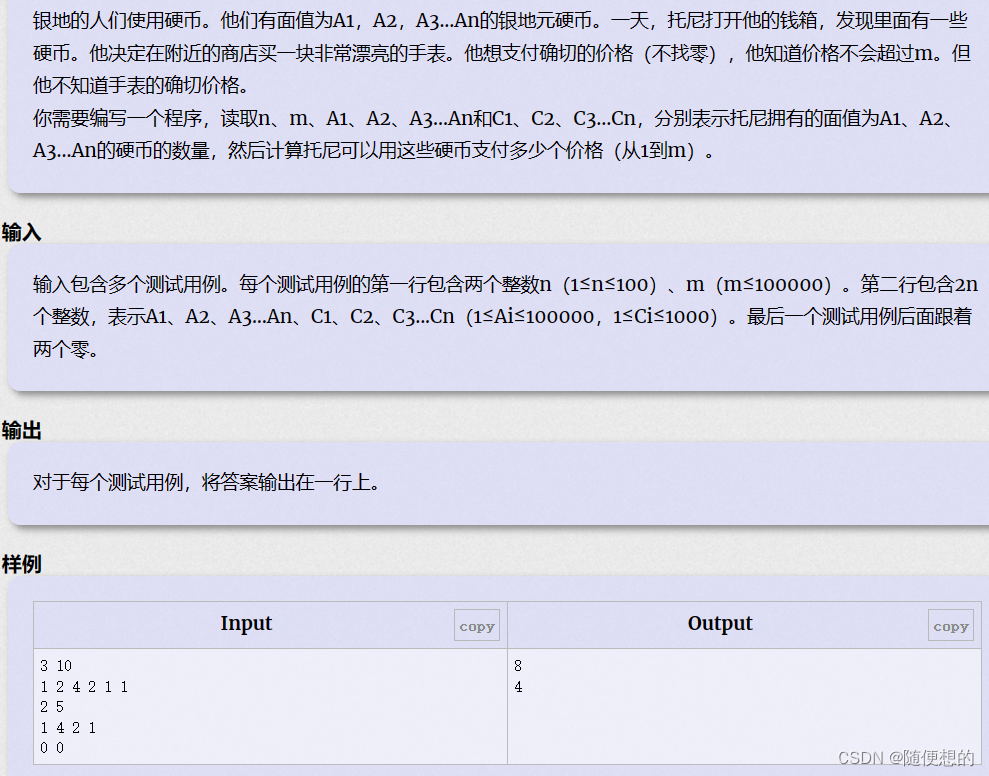
练习题

Coins


#include<iostream>
#include<cstdio>
#include <cstring>
#define ll long long
#define INF 0x3f3f3f3f
using namespace std;
const int N=100;
const int M=100000;
int n,m;
int value[N+1],counts[N+1],nums[M+1];
bool dp[M+1];
 
void solve(){
   memset(dp,false,sizeof(dp));
   int ans=0;
   dp[0]=true;
   for(int i=1;i<=n;i++){
        memset(nums,0,sizeof(nums));
        for(int j=value[i];j<=m;j++){
            if(!dp[j]&&dp[j-value[i]]&&nums[j-value[i]]<counts[i]){
                ans++;
                nums[j]=nums[j-value[i]]+1;
                dp[j]=true;
            }
        }
   }
   printf("%d\n",ans);
}
 
int main()
{
    scanf("%d",&n);
    scanf("%d",&m);
    while(n!=0&&m!=0){
        for(int i=1;i<=n;i++)
            scanf("%d",&value[i]);
        for(int i=1;i<=n;i++)
            scanf("%d",&counts[i]);
        solve();
        scanf("%d",&n);
        scanf("%d",&m);
    }
    return 0;
}

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/很楠不爱3/article/detail/332955