OpenCV4机器学习（八）：决策树原理及分类实战

前言：

本专栏主要结合OpenCV4，来实现一些基本的图像处理操作、经典的机器学习算法（比如K-Means、KNN、SVM、决策树、贝叶斯分类器等），以及常用的深度学习算法。

系列文章，持续更新：

• OpenCV4机器学习（一）：OpenCV4+VS2017环境搭建与配置
• OpenCV4机器学习（二）：图像的读取、显示与存储
• OpenCV4机器学习（三）：颜色空间（RGB、HSI、HSV、Lab、Gray）之间的转换
• OpenCV4机器学习（四）：图像的几何变换、仿射变换
• OpenCV4机器学习（五）：标注文字和矩形框
• OpenCV4机器学习（六）：K-means原理及实现
• OpenCV4机器学习（七）：KNN 原理及实现

---

一、决策树介绍

决策树是一种机器学习的方法，可用于分类或回归问题。它是一种树形结构，可以是二叉树，也可以是非二叉树，其中每个内部节点表示一个属性上的判断，每个分支代表一个判断结果的输出，最后每个叶节点代表一种分类结果。

决策树有许多不同版本，典型版本是最早出现的ID3算法，以及对其进行改进后形成的C4.5算法，这两种算法可用于分类。对ID3算法改进的另一个分支为”分类和回归树“，即CART算法，可用于分类或回归。CART算法为随机森林和Boosting等重要算法提供了基础。在OpenCV中，决策树实现的是CART算法。

其实决策树的分类和人在生活中的决策很相似，举个栗子：

今天我想网购台电脑，刷到一台看着挺带劲的机子，在决定买不买之前，我心路历程是这样的：

1. 这台笔记本价格还可以，7000 多，没超过 8000 ，在我的可接受范围内
2. emmm，牌子是 xxx ，名牌值得信赖。。再看看配置
3. i7，固态+机械，显存 8G，内存16G。这个配置一看就是游戏本，我喜欢。看看评价如何?
4. woc，这么多差评，差评率也太高了。。。告辞告辞

看到没，刚刚的心路历程就是一个决策过程。我通过品牌、价格、配置、差评率等属性来决定“买还是不买 ”。

二、决策树基本原理

决策树分为分类树和回归树两种，分类树对离散变量做决策树，回归树对连续变量做决策树。决策树的概念非常简单，我们在日常生活中也会自然而然地用到。从逻辑角度分析的话，决策树分类器就像判断模块和终止模块组成的树，终止模块表示分类结果（也就是树的叶子节点）。判断模块表示对一个特征取值的判断（该特征有几个值，判断模块就有几个分支）。

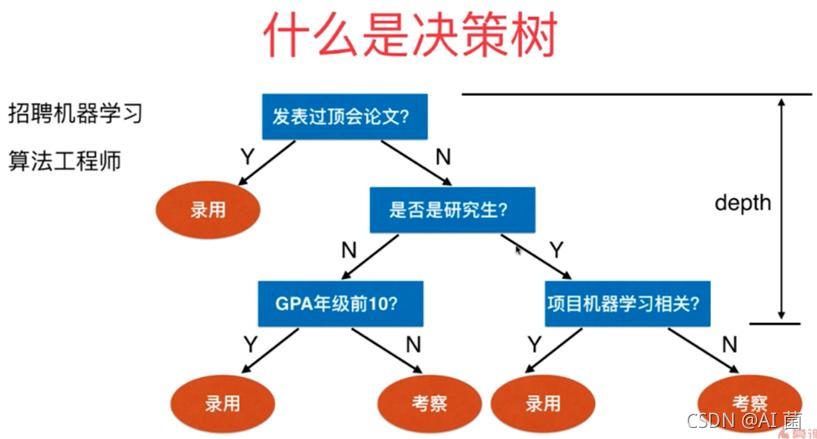
如果不考虑效率，那么样本所有特征的判断级联起来终会将某一个样本分到一个类终止块上。实际上，样本所有特征中有一些特征在分类时起到决定性作用，决策树的构造过程就是找到这些具有决定性作用的特征，将决定性作用最大的那个特征作为根节点，然后递归找到各分支下子数据集中次大的决定性特征，直至子数据集中所有数据都属于同一类。所以，构造决策树的过程本质上就是根据数据特征将数据集分类的递归过程，我们需要解决的一个核心问题就是，当前数据集上哪个特征在划分数据分类时起决定性作用。

三、决策树学习过程

一棵决策树的生成过程主要分为以下3个部分:

• 特征选择：特征选择是指从训练数据中众多的特征中选择一个特征作为当前节点的判断标准，如何选择特征有着很多不同量化评估标准，从而衍生出不同的决策树算法。
• 决策树生成： 根据选择的特征评估标准，从上至下递归地生成子节点，直到数据集不可分则停止决策树停止生长。 树结构来说，递归结构是最容易理解的方式。
• 剪枝：决策树容易过拟合，一般来需要剪枝，缩小树结构规模、缓解过拟合。剪枝技术有预剪枝和后剪枝两种。

三、切分属性的选择

决策树的核心问题是：自顶向下的各个节点应该选择何种属性进行切分，才能获得更好的分类器？因此选择在分类时起到决定性作用的属性是决策树的关键所在。

ID3 算法使用信息增益选择最佳属性构建决策树，即使用能获得最大信息增益的属性作为划分当前数据集的最佳属性。假设属性A对训练数据集D的信息增益为G(D, A)，信息增益计算公式如下：

$G(D,A)=H(D)-H(D|A)$

其中，H(D)是数据集D原始的信息熵，H(D|A)选择属性A作为判断条件下D的条件熵，两者之差即为属性A带来的信息增益。信息增益越大，说明该属性减小混乱的作用越大，即该属性更重要。

信息熵：在概率论中，信息熵给了我们一种度量不确定性的方式，是用来衡量随机变量不确定性的，熵就是信息的期望值。若待分类的事物可能划分在N类中，分别是d1,d2,…,dn，每一种取到的概率分别是p1,p2,…,pn，那么D的熵就定义为:

$H(D)=-{\sum }_{i=1}^n{p}_{i}log{p}_i$

条件熵：假设有随机变量(D|A)，其联合概率分布为:P(D=di,A=ai)=pij,i=1,2,⋯,n;j=1,2,⋯,m。则条件熵H(D|A)表示在已知随机变量D的条件下随机变量A的不确定性，其定义为D在给定条件下A的条件概率分布的熵对D的数学期望:

$H(D|A)=-{\sum }_{i=1}^n{p}_{i}H(D|A=a_i)$

四、决策树的优缺点

决策树的一些优点为：

• 容易理解，可解释性较好
• 可以用于小数据集
• 时间复杂度较小
• 可以处理多输入问题，可以处理不相关特征数据
• 对缺失值不敏感

决策树的一些缺点为：

• 在处理特征关联性比较强的数据时，表现得不太好
• 当样本中各类别不均匀时，信息增益会偏向于那些具有更多数值的特征
• 对连续性的字段比较难预测
• 容易出现过拟合
• 当类别太多时，错误可能会增加得比较快

五、决策树分类实战

下面采用OpenCV中的决策树来对Mushroom数据集进行二分类，判断蘑菇是有毒还是没毒。Mushroom数据集是UCI数据集中的蘑菇可食用数据集，该数据集中一共有8124个蘑菇样本，每一个样本特征向量由22个描述蘑菇外观的属性构成，每个蘑菇被确定为可食用（e）或有毒（p）两类标签。

1、数据集准备

// 1.1读取数据
const char *csv_file_name = argc >= 2 ? argv[1] : "../mushroom/agaricus-lepiota.data";

// 1.2 读取CSV数据文件
cv::Ptr<TrainData> dataSet =
	TrainData::loadFromCSV(csv_file_name, // Input file name
		0, // 从数据文件开头跳过的行数
		0, // 样本的标签从此列开始
		1, // 样本输入特征向量从此列开始
		"cat[0-22]" // All 23 columns are categorical
	);

// 1.3 确定数据总样本数
int n_samples = dataSet->getNSamples();
cout << "从" << csv_file_name << "中，读取了" << n_samples << "个样本" << endl;

// 1.4 划分训练集与测试集
dataSet->setTrainTestSplitRatio(0.9, false); //按90%和10%的比例将数据集为训练集和测试集
int n_train_samples = dataSet->getNTrainSamples();
int n_test_samples = dataSet->getNTestSamples();
cout << "Train Samples: " << n_train_samples << "  Test  Samples: " << n_test_samples << endl;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

2、创建决策树

// 2.1 创建决策树模型
cv::Ptr<RTrees> dtree = RTrees::create();

// 2.2 设置模型参数
dtree->setMaxDepth(10);//10
dtree->setMinSampleCount(10);//10
dtree->setRegressionAccuracy(0.01f);
dtree->setUseSurrogates(false /* true */);
dtree->setMaxCategories(15);
dtree->setCVFolds(1 /*10*/); // nonzero causes core dump
dtree->setUse1SERule(false/*true*/);
dtree->setTruncatePrunedTree(true);
//dtree->setPriors( priors );
dtree->setPriors(cv::Mat()); // ignore priors for now...						
1
2
3
4
5
6
7
8
9
10
11
12
13
14

3、训练决策树

cout << "start training..." << endl;
dtree->train(dataSet);
cout << "training success." << endl;
1
2
3

4、测试

cv::Mat results_train, results_test;
float train_error = dtree->calcError(dataSet, false, results_train);// use training data
float test_error = dtree->calcError(dataSet, true, results_test); // use test data
std::vector<cv::String> names;
dataSet->getNames(names);
Mat flags = dataSet->getVarSymbolFlags();
cout << "[Decision Tree] Error on training data: " << train_error << "%" << endl;
cout << "[Decision Tree] Error on test data: " << test_error << "%" << endl;
1
2
3
4
5
6
7
8

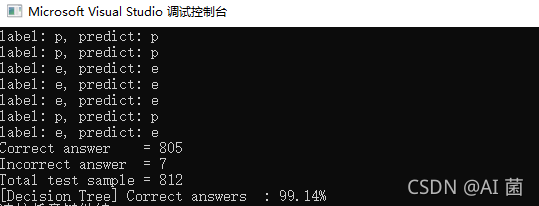
5、统计输出结果

cv::Mat expected_responses = dataSet->getTestResponses();
int t = 0, f = 0, total = 0;
for (int i = 0; i < dataSet->getNTestSamples(); ++i) {
	float responses = results_test.at<float>(i, 0);
	float expected = expected_responses.at<float>(i, 0);
	cv::String r_str = names[(int)responses];
	cv::String e_str = names[(int)expected];
	if (responses == expected)
	{
		t++;
		cout << "label: " << e_str << ", predict: " << r_str << endl;
	}
	else
	{
		f++;
		cout << "label: " << e_str << ", predict: " << r_str << " ×" << endl;
	}
	total++;
}
cout << "Correct answer    = " << t << endl;
cout << "Incorrect answer  = " << f << endl;
cout << "Total test sample = " << total << endl;
cout << setiosflags(ios::fixed) << setprecision(2);
cout << "[Decision Tree] Correct answers  : " << (float(t) / total) * 100 << "%" << endl;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

输出结果：

参考链接：
https://www.cnblogs.com/sxron/p/5471078.html
https://zhuanlan.zhihu.com/p/197476119

戳戳下方二维码，更多干货第一时间送达！