【语音识别】MFCC特征提取

本次笔记主要从原理层面讲述了MFCC特征提取的流程，先是介绍了正弦波的离散化，之后介绍了奈奎斯特采样定理的由来，在讲述傅里叶变换的使用，最后将这些应用于MFCC特征提取算法。

信号与正弦波

高中学过三角函数：
x t = sin(2πf0t)
但是这个图像是连续的，点动成线，而计算机最喜欢处理的就是确切的点，但是一条线上有无数点，需要我们取其中某些点进行计算，而取点就是要考虑到相同间隔，又称：采样频率。
采样周期：ts，其倒数为采样频率fs = 1/ts
而采样点序号为n

从而得到离散化后的公式：
x n = sin(2πf0nts)

这里又会延伸一个新问题，采样频率越高自然越能保留原始波的信息，那么最低可以是多少？
先给结论：采样频率大于信号中最大频率的两倍。
fs/2 ≥ fmax
这就是奈奎斯特采样定理。
即，在原始信号的一个周期内，至少要采样两个点，才能有效杜绝频率混叠问题。

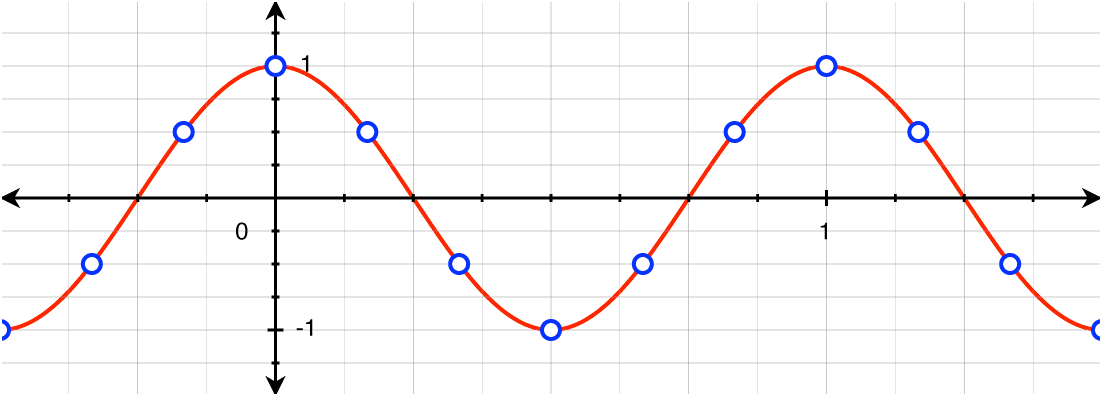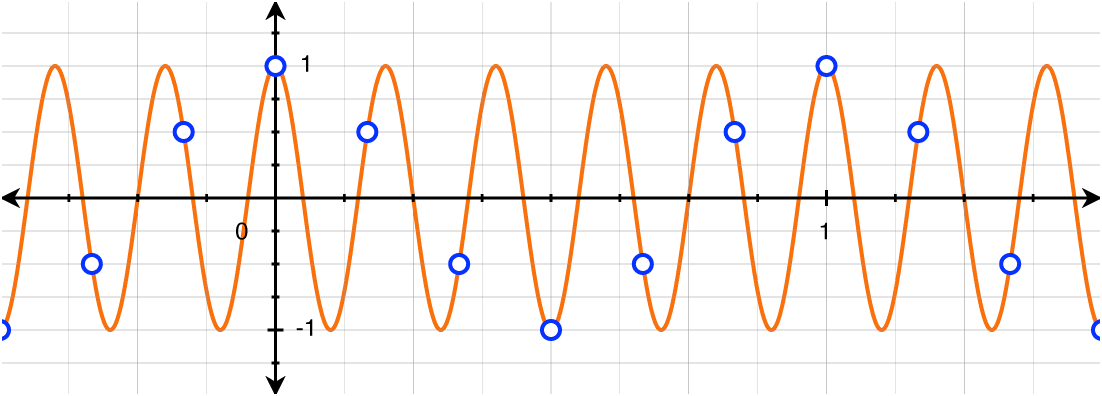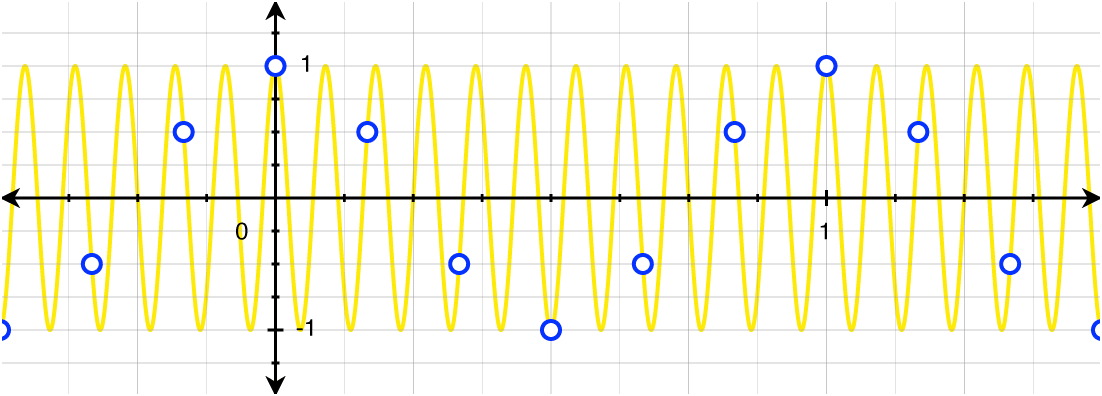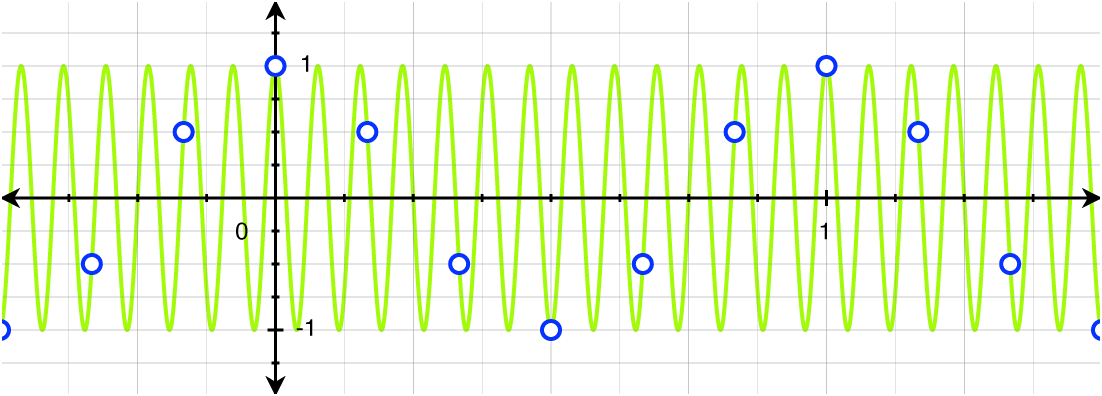
下面思考问题：给出正弦波采样后的离散序列可以恢复之前的正弦波波形吗？
不一定，下图可以直观的表现出来，如果一个周期内采样点少于2，那么会丢失很多信息，最直观的就是周期不同。
这种情况又叫做频率混叠。

离散傅里叶变换

在现实中声音通常是很多正弦波叠加而成，我们看到的波形就像是山水画中的重山叠嶂，如果要分析就需要一点点剥离，这个工作就像是纸雕艺术中剥离一层层的纸。于是我们从正面看要转换到侧面看，也就是从时域转到频域视角，这个操作叫做DFT。

·DFT

定义：给定一个长度为