Logistic Regression(基本原理分析+python代码实现)_python logisticregression() 源码详解

作者：小蓝xlanll | 2024-03-29 22:25:24

踩

python logisticregression() 源码详解

Logistic Regression(基本原理分析+python代码实现)

一、基本理论分析

我们假定我们预测的值为h（hypotheses），真实值为y。

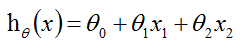（1.1）

theta是参数也叫作权重。从公式（1.1）中可以看到求解h的重点是求解出theta，因为x是给定的已知量。而单个theta的更新公式为：

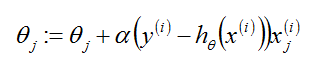（1.2）

其中，j表示第j个theta，i表示向量第i个。

这个更新规则叫作LMS（least mean squares）。就是大家熟悉的Widrow-Hoff学习规则。从（1.2）中我们得到了theta的值，而现在我们又引入了新的未知量alpha。所以，求解的Logistic的重点过程就是围绕给出的(xi,yi)求解alpha值。求解alpha的过程有一个有名的算法叫作梯度上升算法。（更加流行的叫梯度下降算法）下面先给出批量梯度上升算法（batch gradient descent algorithm）

Repeat until convergence{

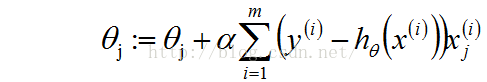(for every j) （1.3）

}

给出该算法对实际数据的分类效果图：

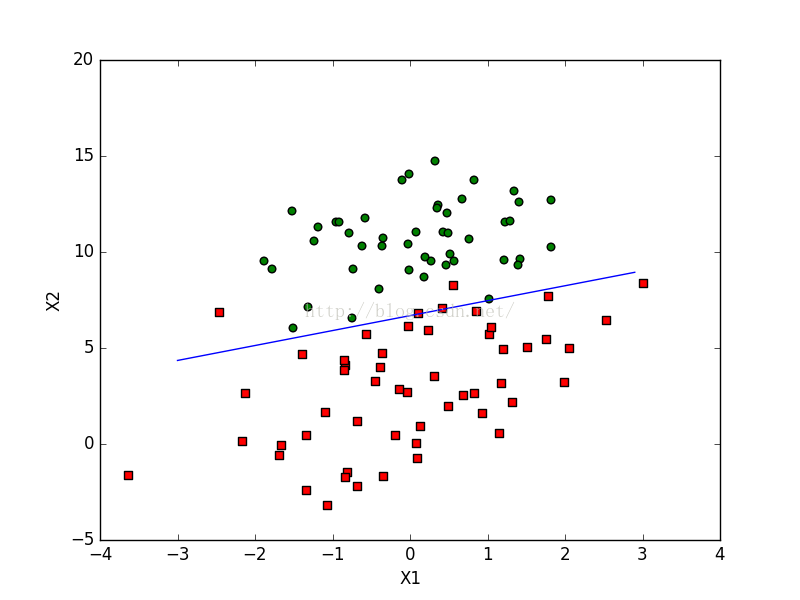
对于批量梯度上升算法的缺陷就是处理小数据还行，可是当处理大数据就有点力不从心了。因为，算法每次都要遍历一遍整个数据。对于该算法的优化算法为随机梯度算法(stochastic gradient descent)。

Loop{

for i =1 to m{

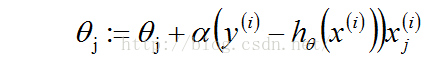（1.4）

}

该算法的实际效果图：

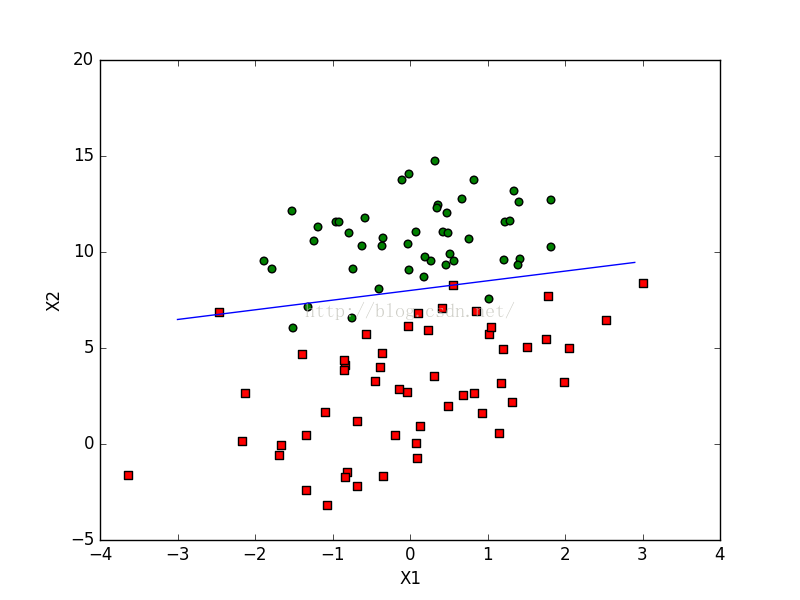
对于优化后的算法是可以在新样本到来时对分类器进行增量式更新，因而是一个在线学习算法。所以，当数据很大的时候就会比上一个算法节省大量的时间。

现在的基本参数都已经解决了。那么问题来了，h是如何得到的呢？其实他是我们选择的一个生成函数，根据我们的选择函数不同其就会有不同的形式。本文所采用的h函数时sigmoid的函数。如下所示：

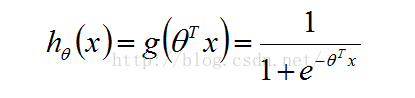（1.5）

二、代码实现部分

（1）、sigmoid函数，公式（1.5）


def sigmoid(inX):
    return 1.0 / (1 + exp(-inX))

（2）、batch gradient descent algorithm，公式（1.3）


#@param dataMatrix type: array
#@param classLabels type: list
#@param weights:alpha's
def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)
    labelMat = mat(classLabels).transpose()
    m, n = shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    weights = ones((n, 1))
    for k in range(maxCycles):              #最大循环次数
        h = sigmoid(dataMatrix * weights)   #矢量
        error = (labelMat - h)              #矢量 
        weights = weights + alpha * dataMatrix.transpose() * error
    return weights

（3）、stachastic gradient descent algorithm，公式（1.4）


#@param dataMatrix type: array
#@param classLabels type: list
#@param weights:alpha's 
def stocGradAscent(dataMatrix, classLabels, numIter = 150):
    m, n = shape(dataMatrix)
    weights = ones(n)
    for j in range(numIter):                                    #最大循环次数
        dataIndex = range(m)
        for i in range(m):                                      #更新每个alphas,m为数据组数
            alpha = 4 / (1.0 + j + i) + 0.01
            randIndex = int(random.uniform(0, len(dataIndex)))  #选取随机更新alphas
            h = sigmoid(sum(dataMatrix[randIndex] * weights))  #标量
            error = classLabels[randIndex] - h                  #标量
            weights = weights + alpha * error * dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights

（4）、分类器


def classifyVector(inX, weights):
    prob = sigmoid(sum(inX*weights))
    if prob > 0.5: return 1.0
    else: return 0.0

（5）、测试算法


def colicTest():
    frTrain = open('horseColicTraining.txt')
    frTest = open('horseColicTest.txt')
    trainingSet = []; trainingLabels = []
    for line in frTrain.readlines():
        currLine = line.strip().split('\t')
        lineArr = []
        for i in range(21):
            lineArr.append(float(currLine[i]))
        trainingSet.append(lineArr)
        trainingLabels.append(float(currLine[21]))
    trainWeights = stocGradAscent1(array(trainingSet), array(trainingLabels), 500)#通过训练数据得到的alpha's
#     return trainWeights, trainingSet, trainingLabels
    errorCount = 0; numTestVec = 0.0
    for line in frTest.readlines():
        numTestVec += 1.0
        currLine = line.strip().split('\t')
        lineArr = []
        for i in range(21):
            lineArr.append(float(currLine[i]))
        if int(classifyVector(array(lineArr), trainWeights)) != int(currLine[21]):
            errorCount += 1
    errorRate = (float(errorCount) / numTestVec)
    print "the error of this test is: %f" % errorRate
    return errorRate
 
def multiTest():
    numTests = 10; errorSum = 0.0
    for k in range(numTests):
        errorSum += colicTest()
    print "after %d iterations the average error rate is: %f" % (numTests, errorSum / float(numTests))

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/小蓝xlanll/article/detail/337708