逻辑回归（Logistic Regression）详解

---

前言

逻辑回归是线性分类器，即线性模型。是否是线性模型取决于决策边界。

---

一、逻辑回归

逻辑回归是一种分类方法，主要用于二分类问题，使用逻辑函数（即Sigmoid函数）。
$$g(z)=\frac{1}{1+e^{-z}}$$
原始的条件概率为（w是设定好的向量矩阵，x是特征表示为的向量，b是偏置项。）
$$p(Y|X)=w^{T}x+b$$
上述两个式子结合，可以将条件概率和逻辑回归联系到一起，则在特征X的条件下，被划分为Y类别的概率是：
$$p(Y|X)=\frac{1}{1+e^{-w^{T}x+b}}$$
Sigmoid函数如图所示：

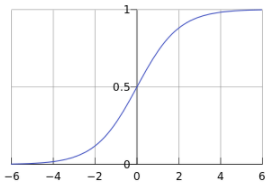
如果是二分类的情况，则有：
$$p(y=1|x,w)=\frac{1}{1+e^{-w^{T}x+b}}$$
$$p(y=0|x,w)=1-p(y=1|x,w)$$
即：
$$p(y=0|x,w)=\frac{e^{-w^{T}x+b}}{1+e^{-w^{T}x+b}}$$
把y=1和y=0的两个式子合并可以得到：
$$p(y|x,w)=p(y=1|x,w{)}^y[1-p(y=1|x,w){]}^{1-y}$$

二、推导目标函数

目的：我们需要最大化目标函数。找出使得目标函数最大的w和b。
引入最大似然：
$$\prod _{i=1}^{m}p(y^i|x^i,w)=\prod _{i=1}^{m}p(y=1|x^i,w{)}^{y^i}[1-p(y=1|x^i,w){]}^{1-y^i}$$
两边取自然对数可得：
$$\sum _{i=1}^m[y^{i}logp(y=1|x^i,w)+(1-y^i)log(1-p(y=1|x^i,w))]$$
最大化原函数等价于求最小化函数：
$$-\frac{1}{m}\sum _{i=1}^m[y^{i}logp(y=1|x^i,w)+(1-y^i)log(1-p(y=1|x^i,w))]$$
将$p(y=1|x^i,w)$表示为：$h(x^i)$
则最终的目标函数为：
$$J（W,b）=-\frac{1}{m}\sum _{i=1}^m[y^{i}logh(x^i)+(1-y^i)log(1-h(x^i))]$$

三、逻辑回归实战

1
2

四、正则化

目的：正则化主要是为了解决过拟合问题。

参考文献：
逻辑回归（目标函数推导）.
机器学习笔记之线性回归、岭回归、Lasso回归.

---

总结