小舞很执着

这个屌丝很懒，什么也没留下！

热门标签

算法我也不知道有没有下一个---一个题目的开端（索引堆与图）

作者：小舞很执着 | 2024-08-07 17:53:44

踩

ab5,bc4,cd8 火车前端

病痛了一周，折磨来折磨去，终于还是平静了下来，现在能把上周末"贯穿"学到的最后一个基础数据结构的知识给沉淀沉淀了。也是即将再单位分享的东西：图论。这东西，想当年大二，学校的时候，只是理解或者画图，就已经很费劲了，当时我们平时作业包括后来的期末考试也只是到理解原理的层面，会画图，就行，实现什么的，根本别想。我自己当年也是认真看过，死磕过几个算法的实现：最小生成树、最短路径等，然而，是看不懂的。这么多年过去了，自己编程能力和见识多了，回过头来，发现，其实并没那么难，只不过比平时的业务逻辑稍微复杂些，但是相较于框架的源码复杂度来说，还是远远够不到的。这一次，我先以一道题开始，逐步将相关的知识点讲下来，采取这种方式，最后，会拓展的讲讲其他的实现，恩，开干

零、一些话

本次的题目，其实算是一道功能实现题，但是能很直接的看出使用的数据结构和大二数据结构课本中介绍的这种数据结构的基本几个之一的算法，所以非常考察当年本科计算机基础的夯实程度与编程实践能力。还是那句话，不要整天咔咔咔的写个curd就觉得会编程，很牛逼。计算机能解决的问题，远远不止curd，编程能力也远远不止curd。同样，这道题，也是一道面试题(具体出处，我就不说了)，成败与否，工资高与低，日子苦逼与否，可能往往取决于一道题，并非危言耸听。有人觉得算法没用，平时用不到，都是api调用，我耗时耗力学，有啥回报呢，我能用来解决什么问题呢？下面我来谈谈我的想法。

算法，我觉得类似于我现在追的一部翻拍武侠剧《倚天屠龙记》中的两部武学经典《九阳神功》与《乾坤大挪移》。张无忌整个过程中似乎并没有学什么具体的武功招式，与外家功夫，只学了这两部内功圣经，就已经干翻六大派高手，干翻赵敏手下的一大堆的援军与玄冥二老，称霸武林。可是这两部武学内功并没有交张无忌一招一式啊！我觉得算法如此。我们现在编程生活中，几乎不用我们去实现链表，更不可能让我们实现一个红黑树，更别提让我们写一个图的深度遍历，因为太多太多的框架都帮助我们实现了。然而，试想一种情况：如果一个开发者，能白板写大顶堆小顶堆，能白板手写红黑树，能立马手动编码实现一道基于数据结构的中等难度的LeetCode上面的习题，难道他不会调用spring的api？难道他不会写个sql去查询数据库？我相信即使他不会，也比一般开发者学的快！更进一步，如果你发现你要根据具体的业务场景实现自己的业务负载均衡模型、在电信的业务模型中对具体的一个表达式进行解析（恩，我弄过）、在游戏开发领域快速判断两点之间的连通性等等这些，都是必须要牢靠掌握数据结构与算法能力的。哪怕是，我们想要更佳平滑的弥补HashMap的多线程坑，不懂数据结构，那是绝对不可能的。

也许百度百度，可能大家都能知道怎么弄。可是自我思考得来的解决与百度来的解决，那是截然不同的两种能力等级！解决问题的速度，也是不一样的。更佳的，当面临系统优化、制定规则引擎、写一些系统工具，那算法与数据结构就是无论如何都无法绕开的了。所以为什么很多大厂面试，为啥愿意面算法，让你手写算法，原因在此。本来就是更上了一个level啊！是否录取一个应聘者，如何开工资，能力等级是多少，高下立判！

一、算法原题

Kiwiland市的铁路系统服务于多个城镇。由于资金问题，所有线路均为“单向线路”。例如，由Kaitaia向Invercargill的方向有一条铁路线，但反方向却没有路线。事实上，即使这两个方向都有铁路线，他们也可能是不同的线路轨迹，里程数也不一定相同。

这道题就是要帮助铁路系统为乘客提供线路信息。具体来讲，你需要计算出某条线路的里程数，两个城镇之间的线路数量以及其中的最短线路。

**Input：**一个有向图（directed graph），其中的节点表示一个城镇，线表示两个城镇间的线路，线的权重表示距离。一条线路不得出现两次或以上，且起点城镇和终点城镇不得相同。

**Output：**测试1至5，如果该线路不存在，则输出 'NO SUCH ROUTE'，否则就按照给定的线路行进，注意不要添加任何其他站点！例如，在下面第1条线路中，必须从A城开始，直接到达B城（距离为5），然后直接到达C城（距离为4）。

线路A-B-C的距离
线路A-D的距离
线路A-D-C的距离
线路A-E-B-C-D的距离
线路A-E-D的距离
从C点开始，在C点结束，沿途最多可以有3个站点，符合该要求的线路有几条？在下面给出的示例数据中，共有2条符合线路：C-D-C (2 站)，C-E-B-C (3 站)
从A点开始，在C点结束，要求线路上必须有4个站点，符合该要求的线路有几条？在下面给出的示例数据中，共有3条符合线路：A 到 C (通过 B,C,D); A 到 C (经过 D,C,D); 以及 A 到 C (经过 D,E,B).
A 到 C的最短路线长度
B 到 B的最短路线长度
从C点开始，在C点结束，要求距离小于30，符合该要求的线路有几条？在下面给出的示例数据中，符合条件的线路有：CDC, CEBC, CEBCDC, CDCEBC, CDEBC, CEBCEBC, CEBCEBCEBC.

测试输入：

在测试输入中，城镇名字由A、B、C、D代表。例如AB5表示从A到B，线路距离为5.

图表: AB5, BC4, CD8, DC8, DE6, AD5, CE2, EB3, AE7

要求输出：

Output #1: 9

Output #2: 5

Output #3: 13

Output #4: 22

Output #5: NO SUCH ROUTE

Output #6: 2

Output #7: 3

Output #8: 9

Output #9: 9

Output #10: 7

从题目可以看出，其实就是要实现一个最简单的图，并最终实现一个最短路径的算法。当然这个过程中，会涉及一些数据结构与算法：堆(索引最小堆)、邻接矩阵表示图、图的深度优先遍历、有环图的遍历、Dijkastra最短路径算法（正权边）。下面会一个个来说。

二、最小堆

首先我们围绕这道题，从最最基础的结构 — 堆，说起。以往，各种教学，都从大顶堆讲，然后自己私下去拓展学小顶堆，这回我们直接从小顶堆，来入手。首先让我们看看堆的定义（来源于维基百科）：

堆（英语：Heap）是计算机科学中的一种特别的树状数据结构。若是满足以下特性，即可称为堆：“给定堆中任意节点 P 和 C，若 P 是 C 的母节点，那么 P 的值会小于等于（或大于等于） C 的值”。若母节点的值恒小于等于子节点的值，此堆称为最小堆（min heap）；反之，若母节点的值恒大于等于子节点的值，此堆称为最大堆（max heap）。在堆中最顶端的那一个节点，称作根节点（root node），根节点本身没有母节点（parent node）。

总结下：

树状结构
完全二叉(多叉)树(除了叶子节点，其他节点必须所有孩子都有值)
任意父亲节点大于(小于)或者等于孩子节点
大于：最大堆；小于：最小堆

下面是堆的基础模型图：

最小堆的示意图

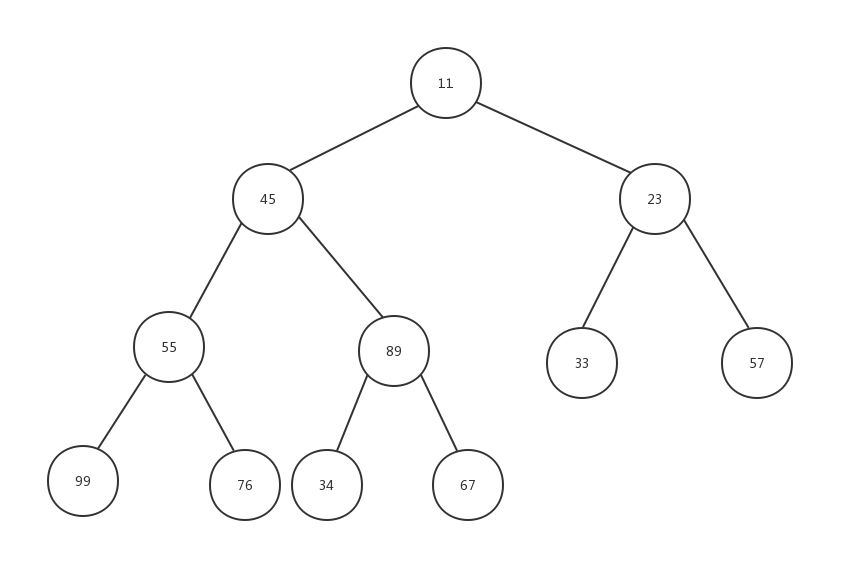
相应的，我们使用的存储堆的数据结构，更多的使用一个数组，如下：

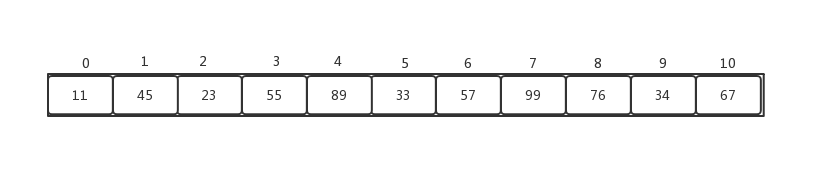
使用数组具体的母子节点的换算公式是：

获取当前节点的父亲节点索引：parentNodeIndex = (currentNodeIndex-1)/2
获取当前节点的孩子索引：
- 左孩子：leftNodeIndex = currentNodeIndex*2 + 1
- 右孩子：rightNodeIndex = currentNodeIndex*2 + 2

下面是我总结的大体上堆这种数据结构的优点：

快速的获取最大(最小)值：O(1)复杂度
简单、快速的底层存储逻辑
堆排序（O(nlogn)）

三、最小堆的核心实现(基于Java)

先给出基础的骨架代码


public class MinPriorityQueue<K extends Comparable<K>> {
 
  	// 堆的基础存储数据结构
    private Object[] elements;
 
  	// 当前堆中元素个数
    private int size;
  
    public MinPriorityQueue() {
        this.elements = new Object[Common.INIT_SIZE];
        this.size = 0;
    }
 
   private void checkLength(int index) {
        if (index < 0 || index >= this.elements.length) {
            throw new IllegalArgumentException("超出限制");
        }
    }
 
    public int lchild(int index) {
        checkLength(index);
        return (index * 2) + 1;
    }
 
    public int rchild(int index) {
        checkLength(index);
        return (index * 2) + 2;
    }
 
 
    public int parent(int index) {
        checkLength(index);
        return (index - 1) / 2;
    }
 
    public void swap(int i, int j) {
        checkLength(i);
        checkLength(j);
 
        K temp = (K) elements[i];
        elements[i] = elements[j];
        elements[j] = temp;
    }
 
    @Override
    public String toString() {
        return "MinPriorityQueue{" +
                "elements=" + Arrays.toString(elements) +
                ", size=" + size +
                '}';
    }
}

有几点：

内部存储由于擦除原因，使用了Object
每个泛型参数类型都要是可比较类型(Comparable)，因为要比较父子节点大小
size表示当前堆中元素大小
当然，这里可以直接使用Comparable类型的基础数组存储

1、上浮操作与添加元素

上浮是保证整个堆保证原先数据规则的一种手段，主要用于添加元素的时候，每次添加元素，我们会直接放到内部基础数组最后一个索引位置，然后做上浮操作，下面我们随便添加一个数字（9），然后看看整体上浮过程是如何变化的：

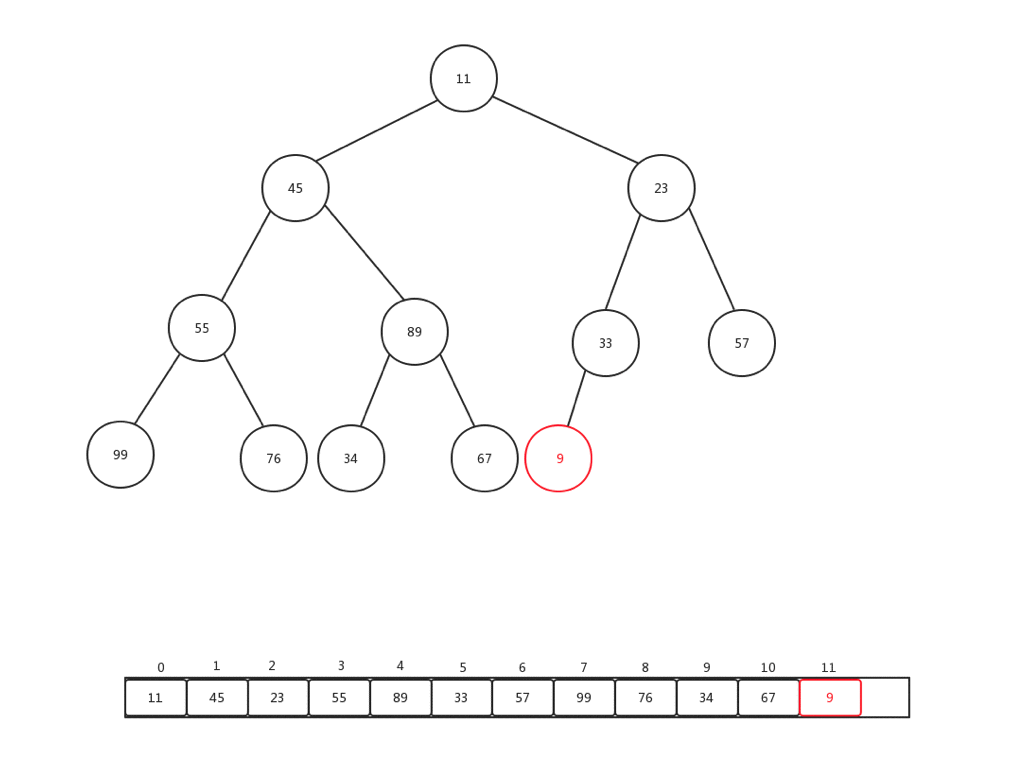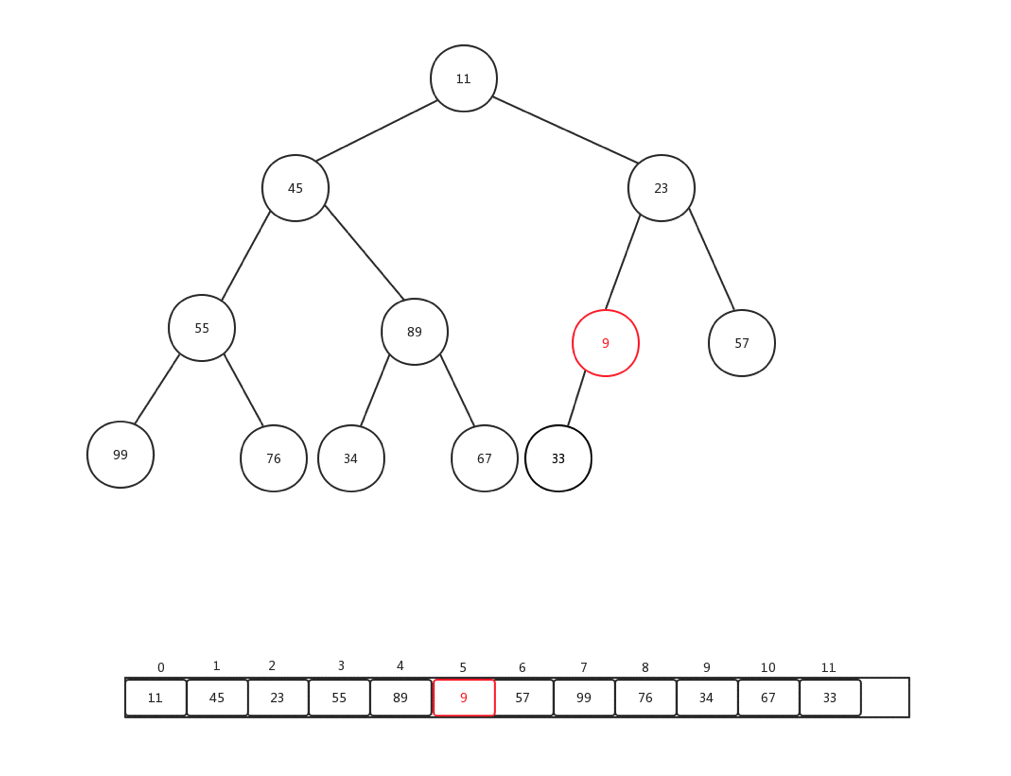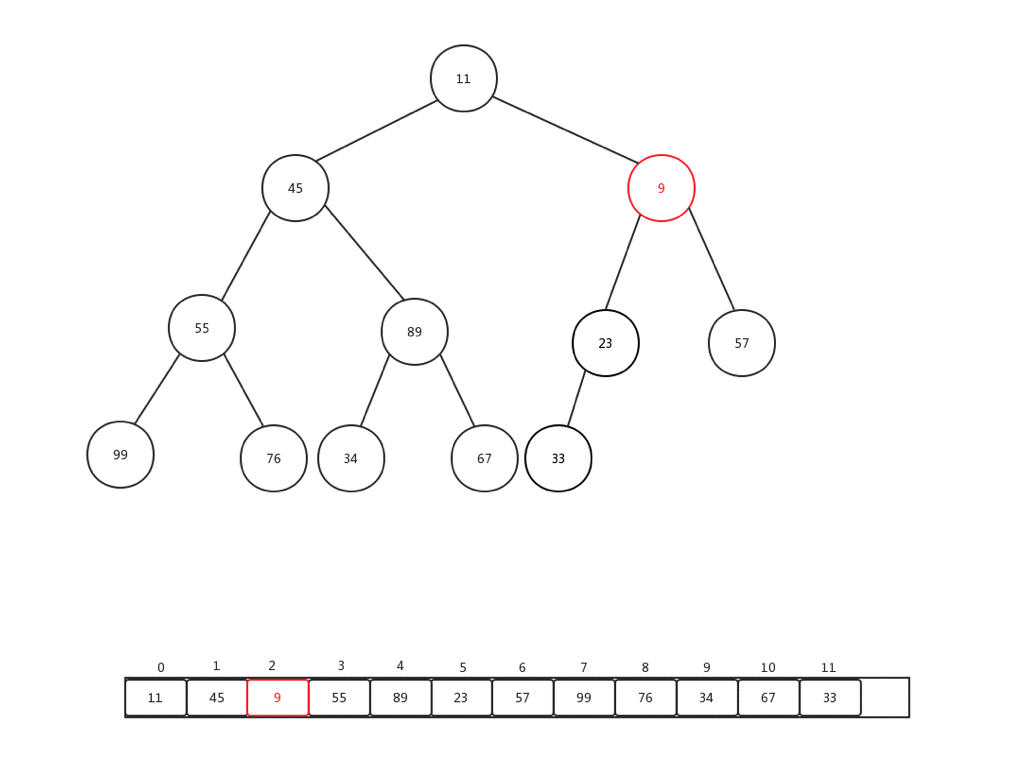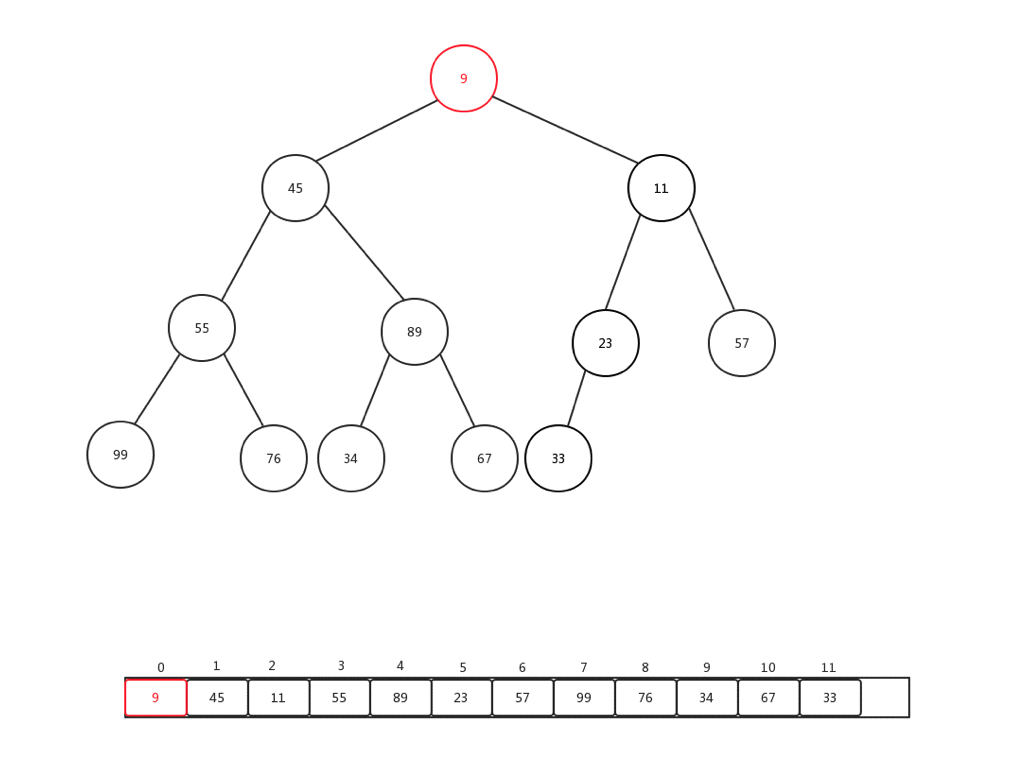
整个过程比较简单，主要是当前节点和父亲加点比较：


		/**
     * 上浮
     */
    public void swam(int index) {
				// 防止索引溢出
        checkLength(index);
 
        int p = index;
        while (p > 0) {
            K currentEle = (K) elements[p];
            int parentIndex = parent(p);
          	// 核心，用于比对当前节点与父亲节点的大小
            if (currentEle.compareTo((K) elements[parentIndex]) < 0) {
              	// 交换当前索引与父亲节点索引中的值
                swap(p, parentIndex);
                p = parentIndex;
            } else {
              	// 一旦发现当前值大于父亲节点，就停止循环
                break;
            }
        }
    }

有了上浮操作，那么向堆中添加元素的代码也是比较简单的了：


		/**
     * 添加元素
     */
    public void addElement(K element) {
        if (size == elements.length) {
            // 添加堆的容量
            resize();
        }
        elements[size] = element;
        swam(size);
      	// 维护当前堆数量大小
        size++;
    }
		/**
     * 扩容
     */
    public void resize() {
        int length = elements.length;
        Object[] tempArr = new Object[length + Common.GROW_SIZE];
        System.arraycopy(elements, 0, tempArr, 0, length);
        this.elements = tempArr;
    }

2、下沉操作与删除元素

相对比较来说，下沉会更加复杂一些，复杂点在于，每次都要进行当前节点与几个孩子节点的比较操作，可是当前节点是否有孩子节点，还是要判断的。总的来说，要花心思去保护索引溢出的情况。首先，让我们看看删除一个堆内元素是如何进行的：

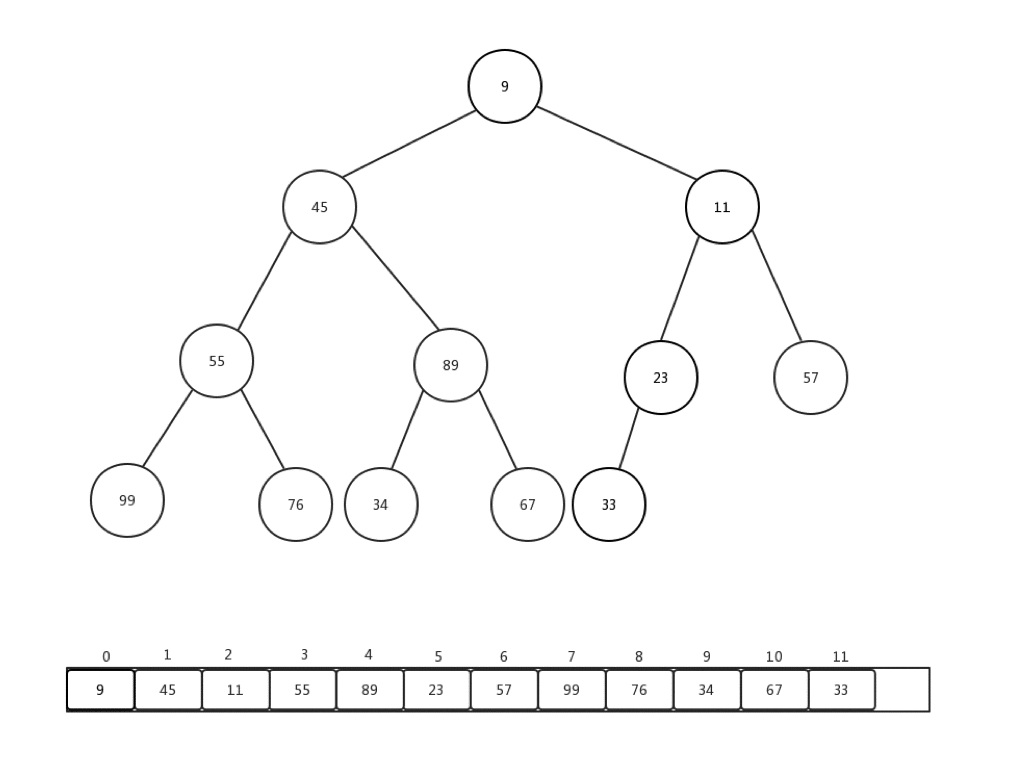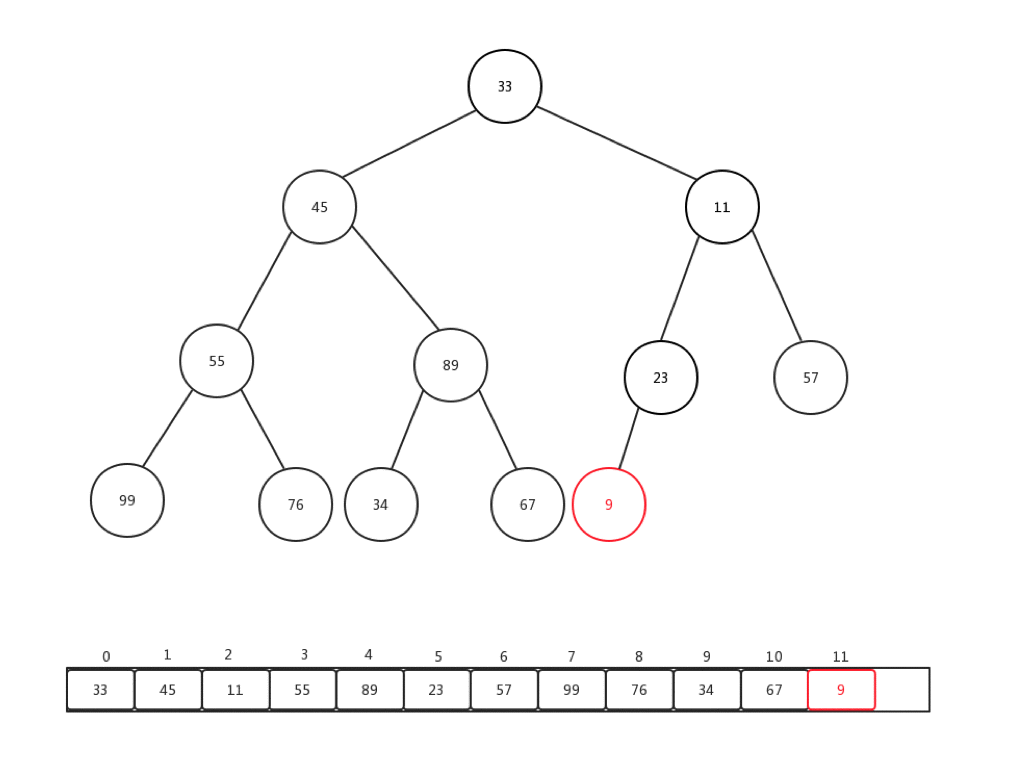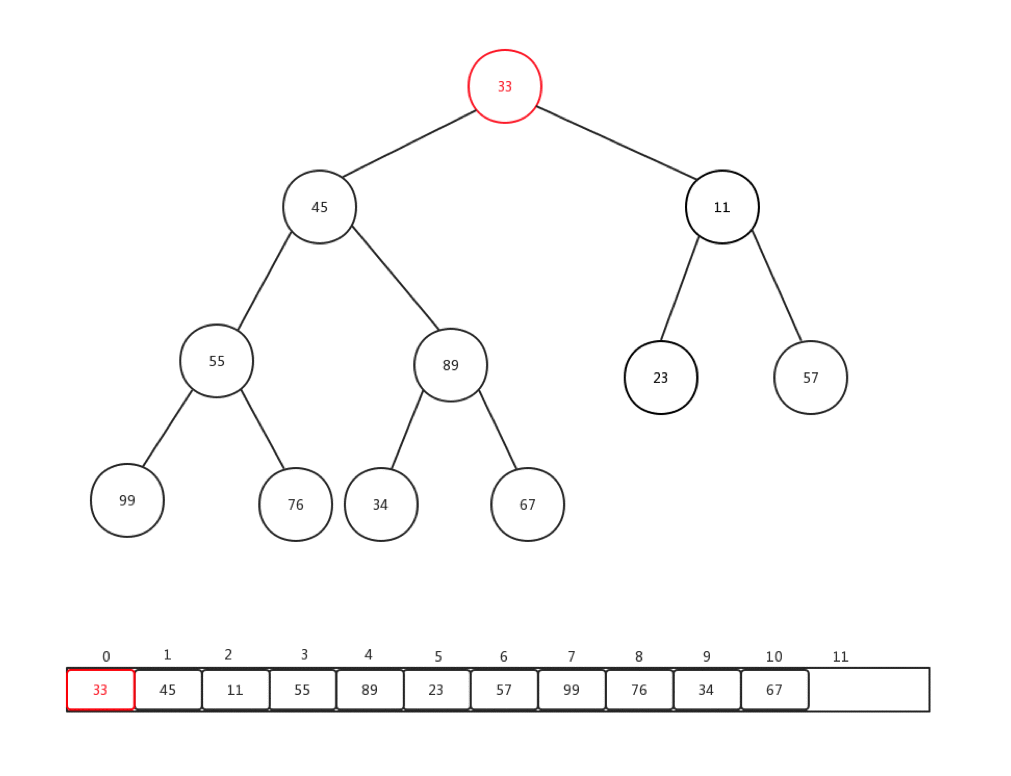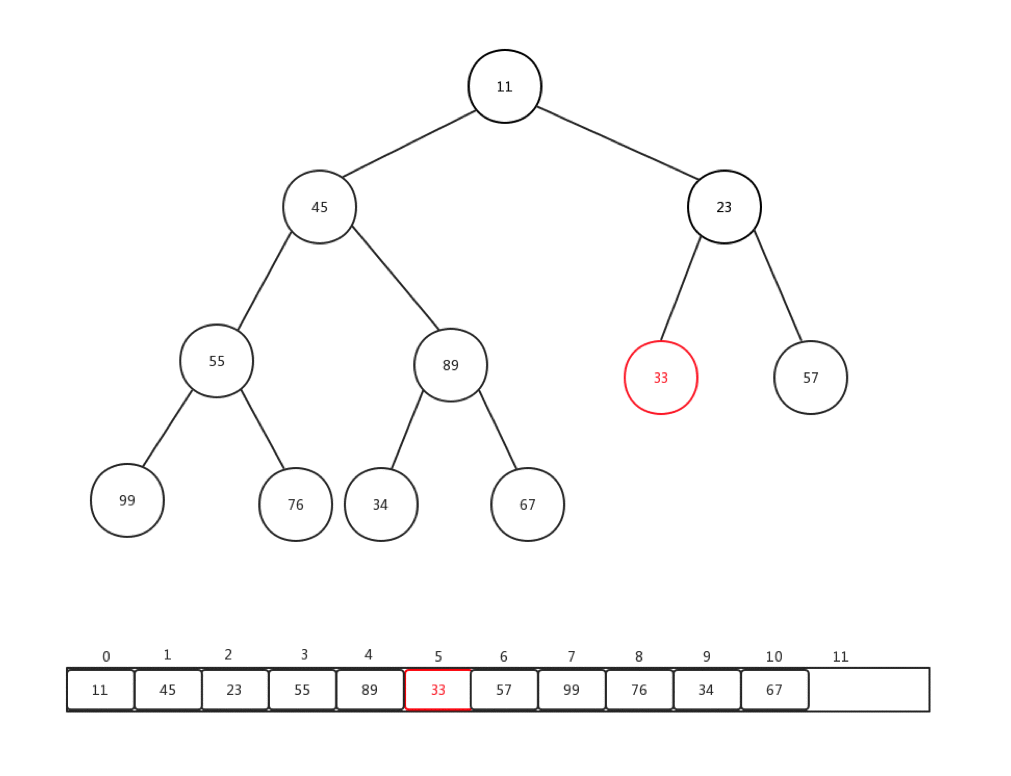
保存堆顶元素的值
交换堆顶和最后的结点
删除最后一个节点的值，指向null
对堆顶(索引为0)做下沉操作

下面是下沉操作的基础代码：


		/**
     * 下沉
     */
    public void sink(int index) {
        checkLength(index);
        int p = index;
        /**
         * 如果左孩子大于或者等于当前堆中元素个数的话，
         * 表明当前节点已经是叶子节点，可以不用继续遍历了
         */
        while (p < size && lchild(p) < size) {
            K currentEle = (K) elements[p];
            // 获取左孩子索引
            int lchild = lchild(p);
            // 获取右孩子索引
            int rchild = rchild(p);
            // 获取左孩子的值
            K lelement = (K) elements[lchild];
            // 获取右孩子的值
            K relement = (K) elements[rchild];
            // 核心，获取左右孩子最小值的那个节点索引，注意，这里右孩子有可能为空
            int minChildIndex = Objects.isNull(relement) ? lchild :
                    (lelement.compareTo(relement) > 0 ? rchild : lchild);
            // 使用当前节点值与最小值比较，如果当前值还要小，那就交换
            if (currentEle.compareTo((K) elements[minChildIndex]) > 0) {
                swap(p, minChildIndex);
                p = minChildIndex;
            } else {
                break;
            }
 
        }
    }

在这里，主要对节点索引进行了详尽的判断与保护，接下来，就是删除元素的方法代码：


 		/**
     * 删除堆顶元素
     */
    public K delElemet() {
        if(size == 0){
            throw new IllegalArgumentException("当前堆已经空了");
        }
        K result = (K) elements[0];
        if (size > 1) {
            swap(0, size - 1);
            elements[--size] = null;
            sink(0);
        } else {
            size--;
        }
        return result;
    }

3、调整数组成为一个最小堆

通常情况下，我们接收到的是一整个数组的值，然后需要我们整理，才能变成一个最小堆，这个过程我们称它为：heapify。就是重新调整。让我们来看下一组数组Integer[] arr = {90,34,99,57,11,67,55,23,76,33,45}如何进行从新调整的：

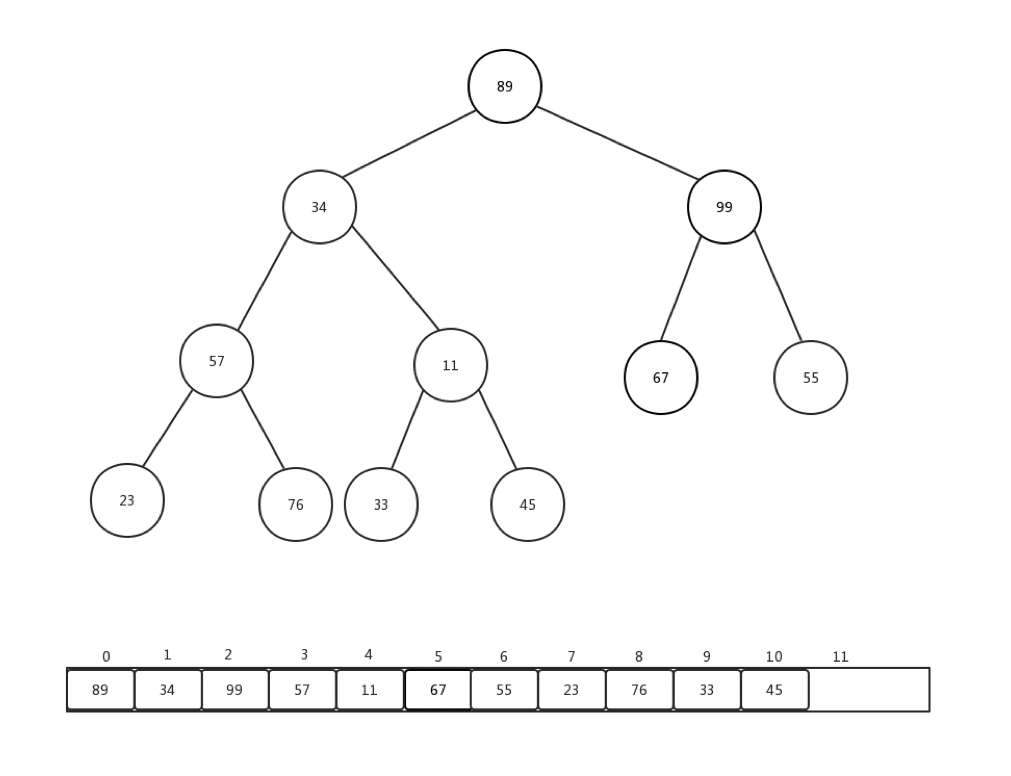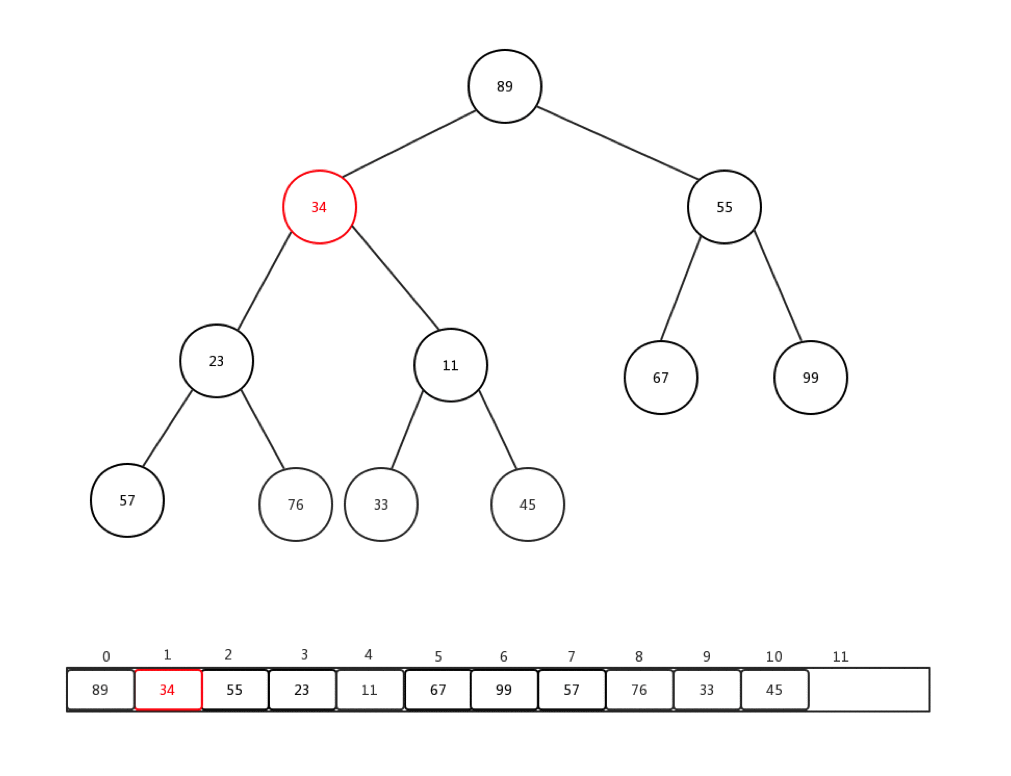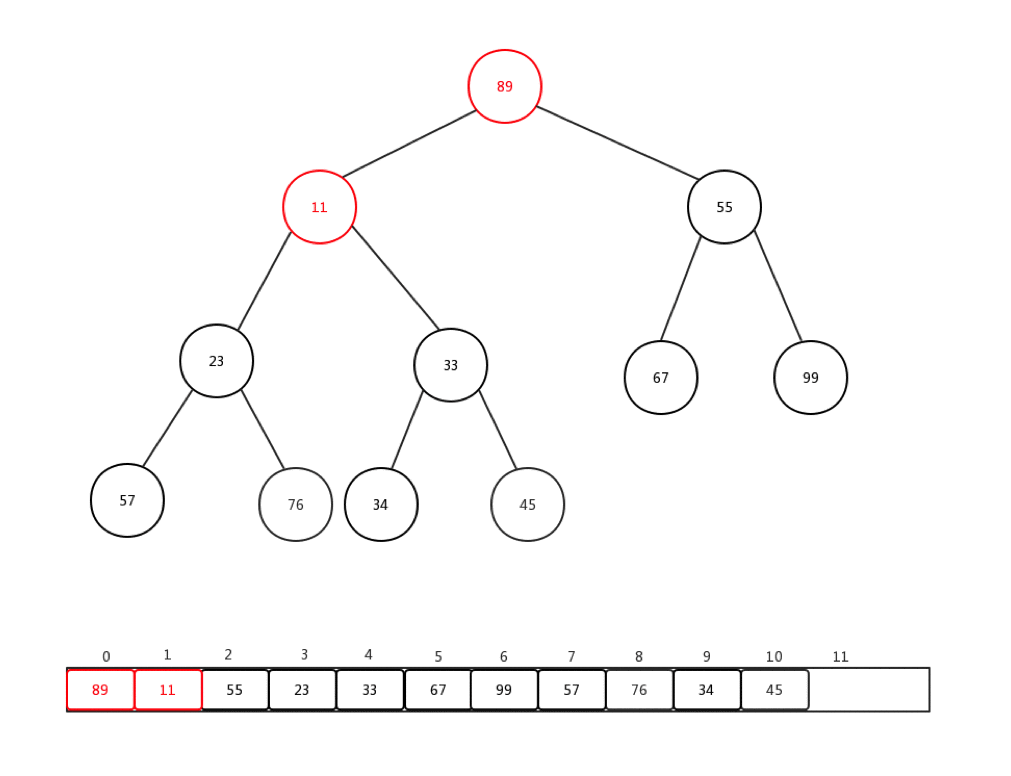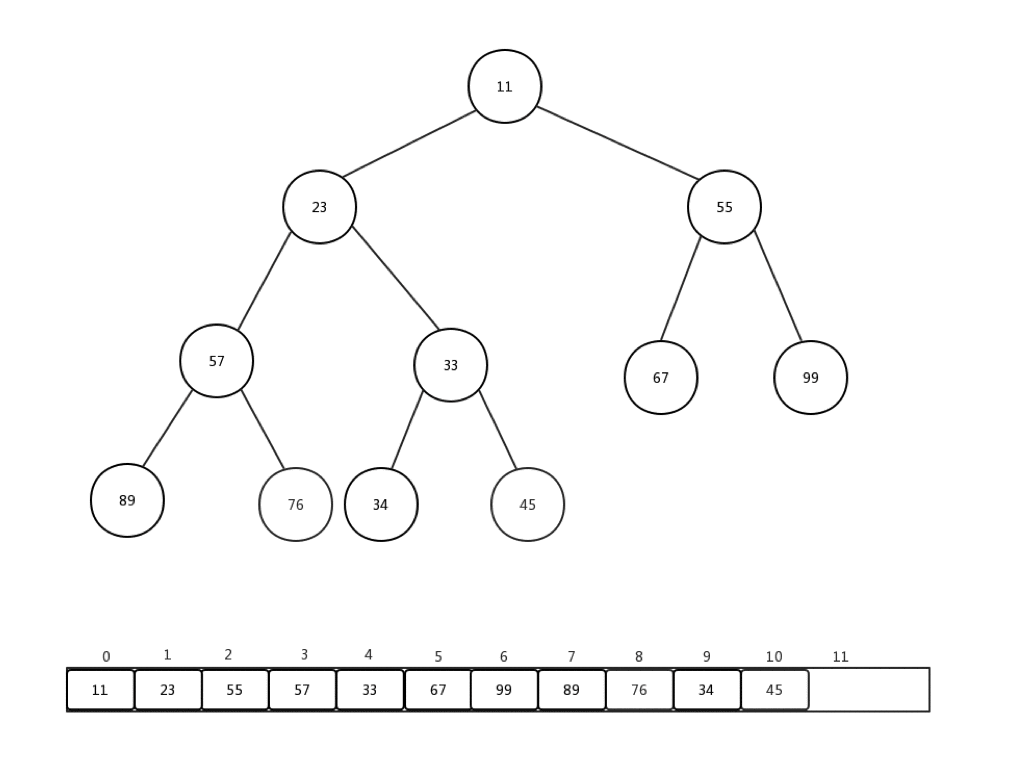
做一些介绍：

每次从第一个非叶子节点开始进行每个节点的下沉操作
第一个非叶子节点的索引 = (最后一个节点索引-1)/2
整体时间复杂度是：O(n)

下面就是基础的代码实现：


	// 每次传入数组的大小	
	public MinPriorityQueue(Comparable[] comps) {
        if (Objects.isNull(comps) || comps.length == 0) {
            throw new IllegalArgumentException("数组不能为空");
        }
        this.elements = new Object[comps.length];
        this.size = 0;
        for (int i = 0; i < comps.length && comps[i] != null; i++) {
            this.elements[i] = comps[i];
            this.size++;
        }
	      heapify();
    }
 
    private void heapify() {
        if (this.size == 0) {
            return;
        }
        int index = (this.size - 2) / 2;
        for (int i = index; i >= 0; i--) {
          	// 下沉
            sink(i);
        }
    }

到此，我们对于一个最小堆的全部实现，就完成了。下面开始介绍基于堆的一种拓展数据结构 — 索引最小堆

四、索引最小堆

经历了最小堆的"洗礼"，发现如下几个问题：

每次交换都是使用原始元素进行交换
没提供修改固定索引元素的方法
如果每个节点元素是一个复杂且庞大的值，那么交换过程会导致很多问题(慢、内存溢出)

就此，索引堆概念出现了：

每个实际元素的数组中的索引位置不变
另申请一个与堆同等大小的数组，存储每个元素在堆中实际位置
再来一个同等大小的数组，反向索引具体堆中的位置(数组索引 —> 堆上的索引)

(最后一点最不好理解，后面会有介绍)如此一来，每次元素添加到堆中，具体的元素就不会随着上浮下沉而变换位置，真正变换的，是索引值(就是一个整型)。

1、索引最小堆演示

下面我根据上面最小堆，进一步扩展成索引最小堆，一步步演示，我们使用的原始数组是：

Integer[] arr = {90,34,99,57,11,67,55,23,76,33,45}

(1)不加反向索引

可以看到全程没有进行存储元素的移动，全部是元素所对应的索引值进行移动，这样一来，就能很好的解决上面元素复杂，移动缓慢的问题。

(2)加上反向索引

上面的索引堆还存在一个问题，就是，我更改堆中对应一个具体索引的元素值，之后，我并不知道这个值对应的具体在堆中的位置，例如：

改变索引4中元素11的值：data[4] = 12
我们想要确定11这个元素堆中的位置(其实是在索引数组的第一个位置上，就是0上面)
然后根据这个位置，对这个位置前面的进行上浮操作，这个位置后面的进行下沉操作，这样就能从新调整堆

这个时候，反向索引就有用了！我下面展现下最终加上反向索引的最终形式：

如果i表示具体索引值，recs表示反向索引数组，indexes表示索引数组，这几个的关系是：

recs[indexes[i]] = i
indexes[recs[i]] = i

反向数组不太好理解，可以多看看，多看看。其实就是一个存储当前索引对应的数据，在堆中的位置，这个位置其实也是一个索引，只不过这个索引指向的是索引数组

2、索引最小堆的基础实现

首先是基础框架的代码：


public class IndexMinPriorityQueue<K extends Comparable<K>> {
		// 索引数组
    private int[] indexes;
		// 原始数据的数组
    private Object[] elements;
		// 反向索引数组
    private int[] recs;
		// 当前堆元素的大小
    private int size;
 
    public IndexMinPriorityQueue() {
        this.indexes = new int[Common.INIT_SIZE];
        this.elements = new Object[Common.INIT_SIZE];
        this.recs = new int[Common.INIT_SIZE];
        this.size = 0;
        for (int i = 0; i < Common.INIT_SIZE; i++) {
            this.indexes[i] = -1;
            this.recs[i] = -1;
        }
    }
 
    public IndexMinPriorityQueue(int count) {
        this.indexes = new int[count];
        this.elements = new Object[count];
        this.recs = new int[count];
        this.size = 0;
        for (int i = 0; i < count; i++) {
          	// 默认初始化时候，堆内没有元素时候两个索引数组的每个字段都初始化成-1
            this.indexes[i] = -1;
            this.recs[i] = -1;
        }
    }
}

加入了两个辅助性质的数组，我们来看看其他的一些修改点，首先是交换数据的方法：


		public void swap(int i, int j) {
        if (i < 0 || i >= size) {
            throw new IllegalArgumentException("超出限制");
        }
        if (j < 0 || j >= size) {
            throw new IllegalArgumentException("超出限制");
        }
				// 可以看到，每次只交换索引数组中的值，真实数据数组不变
        int temp = indexes[i];
        indexes[i] = indexes[j];
        indexes[j] = temp;
 
        // 反向索引数组内部值的确认
        recs[indexes[i]] = i;
        recs[indexes[j]] = j;
    }

相应的，上浮与下沉的方法也是要变动的：


		/**
     * 下沉
     */
    public void sink(int index) {
        if (index < 0 || index > size) {
            throw new IllegalArgumentException("超出限制");
        }
        int p = index;
        while (p < size && lchild(p) < size) {
          	// 可以看到，每次取元素，都是要据具体的索引数组的值来定位真实数据数组的位置
            K currentEle = (K) elements[indexes[p]];
            int lchild = lchild(p);
            int rchild = rchild(p);
            K lelement = (K) elements[indexes[lchild]];
          	// 索引数组的值为-1，表示当前元素被删除或者就是没存入
            int minChildIndex = indexes[rchild] == -1 ? lchild :
                    (lelement.compareTo((K) elements[indexes[rchild]]) > 0 
                     ? rchild : lchild);
            if (currentEle.compareTo((K) elements[indexes[minChildIndex]]) > 0) {
                swap(p, minChildIndex);
                p = minChildIndex;
            } else {
                break;
            }
 
        }
    }
 
    /**
     * 上浮
     */
    public void swam(int index) {
        if (index < 0 || index >= size) {
            throw new IllegalArgumentException("超出限制");
        }
        int p = index;
        while (p > 0) {
            K currentEle = (K) elements[indexes[p]];
            int parentIndex = parent(p);
            K pelement = (K) elements[indexes[parentIndex]];
            if (Objects.nonNull(pelement) && currentEle.compareTo(pelement) < 0) {
                swap(p, parentIndex);
                p = parentIndex;
            } else {
                break;
            }
        }
 
    }

添加是对添加蒜素的修改：


    /**
     * 添加元素
     */
    public void addElement(K element) {
        if (size == elements.length) {
            // 扩容
            resize();
        }
        // 索引数组的末尾添加这个元素的索引值
        indexes[size] = size;
        // 反向索引也是最后一位添加
        recs[size] = size;
        // 其实这也是最后一位添加，因为此时indexes[size] = size
        elements[indexes[size]] = element;
        // 先对最后一位的索引进行上浮操作，然后再将size加一
        swam(size++);
    }
 
		/**
     * 扩容
     */
    public void resize() {
        int length = elements.length;
        Object[] tempArr = new Object[length + Common.GROW_SIZE];
        int[] tempIndexes = new int[length + Common.GROW_SIZE];
        int[] tempRecs = new int[length + Common.GROW_SIZE];
        System.arraycopy(elements, 0, tempArr, 0, length);
        System.arraycopy(indexes, 0, tempIndexes, 0, length);
        System.arraycopy(recs, 0, tempRecs, 0, length);
        for (int i = length; i < tempIndexes.length; i++) {
            tempIndexes[i] = -1;
            tempRecs[i] = -1;
        }
        this.elements = tempArr;
        this.indexes = tempIndexes;
        this.recs = tempRecs;
    }

下面看看删除一个堆顶元素的修改：


		/**
     * 删除堆顶元素
     *
     * @return 堆顶的具体元素值
     */
    public K delElemet() {
        K result = (K) elements[indexes[0]];
        delEl();
        return result;
    }
 
    /**
     * 删除堆顶元素
     *
     * @return 堆顶的具体元素索引值
     */
    public int delElemetIndex() {
        int result = indexes[0];
        delEl();
        return result;
    }
 
    private void delEl() {
        if (size > 1) {
            // 这里其实是交换索引数组的第一位和最后一位的值
            swap(0, size - 1);
        }
        // 此时要把末尾的索引值对应的元素置空，代表删除原始数据
        elements[indexes[--size]] = null;
        // 当然，反向索引数组的值也要删除，置位-1
        recs[indexes[size]] = -1;
        // 当然，最后要把索引数组值删除，其实就是最后一位
        indexes[size] = -1;
        // 对索引数组，就是第一位开始，做下沉
        sink(0);
    }

最后的最后，我们就可以看看如何修改一个堆中的元素了


		public void change(int index, K element) {
        if (index < 0 || index > size) {
            throw new IllegalArgumentException("超出限制");
        }
        this.elements[index] = element;
        // 这时候，反向索引数组就显示作用了：获取这个修改值对应的堆中的索引值
        int currentHeapIndex = this.recs[index];
        swam(currentHeapIndex);
        sink(currentHeapIndex);
    }

五、图的基础

好吧，到了图这里，已经深入到计算机科学领域了，我作为一个工程狗，真心无法，也没有能力一箭到底！所以在此，我先上定义，然后我们截取最简单，切合具体的实际问题(这里就是第一章那道题)来说相关的图论的基础结构与算法，其他的，有关图论的东西太多太多，有兴趣可以自己深入研究。下面是wiki上面的一个定义：

图有多种变体，包括简单图、多重图、有向图、无向图等，但大体上有以下两种定义方式。

二元组的定义

一张图 $G$ 是一个二元组 $(V,E)$ ，其中 $V$ 称为顶点集， $E$ 称为边集。它们亦可写成 $V(G)$ 和 $E(G)$ 。 $E$ 的元素是一个二元组数对，用 $(x,y)$ 表示，其中 $x,y \in V$ 。

三元组的定义

一张图 $G$ 是一个三元组 $(V,E,I)$ ，其中 $V$ 称为顶集（Vertices set）， $E$ 称为边集（Edges set）， $E$ 与 $V$ 不相交； $I$ 称为关联函数， $I$ 将 $E$ 中的每一个元素映射到 $V\times V$ 。如果 $I(e)=(u,v) (e\in E, u,v \in V)$ 那么称边 $e$ 连接顶点 $u,v$ ，而 $u,v$ 则称作 $e$ 的端点， $u,v$ 此时关于 $e$ 相邻。同时，若两条边有一个公共顶点，则称关于相邻。

恩，说实话，我也看不懂，具体对于我们这次要解决的实际问题，相关的数据结构的知识点，提取出以下几点：

我们要实现一个有向图
而且是有向加权图
会有环
边用E(edge)来表示
节点用V(Vertices)来表示
我们这里固定使用一种表示方法来进行图的存储：邻接表

下面我们就开搞！

1、有向图

我们来看看题目中，要我们实现的有向图的基本输入是：

AB5, BC4, CD8, DC8, DE6, AD5, CE2, EB3, AE7

根据此文字表述，我们画出如下的示意图：

有话说：不要在意边的长短与权值大小的对应比例，只是一种展示、展示、展示！

接下来我们就用代码来实现相应的V(定点)与E(边)


// 定点的抽象数据定义
public interface IVertices<V> {
  	// 获取这个节点的值
    V getData();
  
  	// 获取当前节点的索引值
  	int getIndex();
}
 
// 边的抽象数据定义
public interface IEdge<V> {
		// 获取一条边起始顶点的对象
    V getV1();
		// 获取一条边结束顶点的对象
    V getV2();
		// 获取一条边的权值
    int getWeight();
}

2、邻接表存储表示法

最常用的图的表示法有两种：邻接矩阵、邻接表。响应的适用场景如下：

邻接矩阵：适用于稠密图
邻接表：适用于稀疏图

一般来说，我们解决实际问题，都是稀疏图，所以常用邻居表，本次我们只看邻接表的表示法，来存储一个图。下面是基本的邻接表示意图：

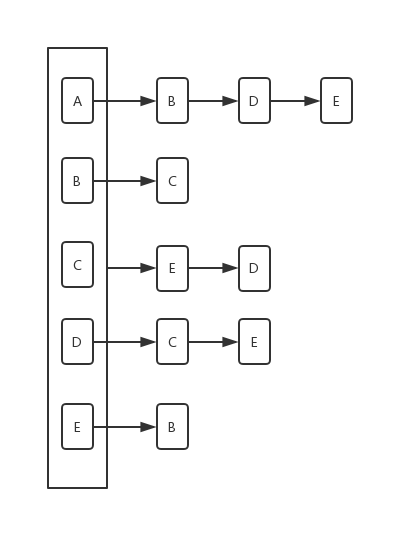
根据上面这个图的展示，整个图使用邻接表存储，会有下面的几点：

一个图对象保存一个map
key值是图中的顶点
value值是list，list中的每个值是以key值顶点为起始的边
顶点对象要实现hashCode与equals方法，因为要当key

下面就是一个图的基本代码实现，使用邻接表的方式：


public class Graph<V extends IVertices, E extends IEdge<V>> {
 
    // 当前图中的结点数目
    private int vsize;
 
    // 当前图中的边的数目
    private int esize;
 
  	// 邻接表
    private Map<V, List<E>> vectors;
 
    public Graph() {
        this.vsize = 0;
        this.esize = 0;
        this.vectors = new HashMap<>();
 
    }
 
  	// 根据所有的结点来初始化
    public Graph(V[] datas) {
        if (Objects.isNull(datas) || datas.length == 0) {
            throw new IllegalArgumentException("初始化失败");
        }
        this.vsize = datas.length;
        this.esize = 0;
        this.vectors = new HashMap<>();
        for (int i = 0; i < this.vsize; i++) {
            this.vectors.put(datas[i], new LinkedList<>());
        }
    }
 
		// 添加一条边
    public void addEdge(E w) {
        List<E> ts = this.vectors.get(w.getV1());
        if (ts == null) {
            throw new IllegalArgumentException("这个节点不存在");
        }
        if (!ts.contains(w)) {
            ts.add(w);
            this.esize++;
        }
    }
 
    // 获取总节点数
    public int getVsize() {
        return vsize;
    }
 
    // 获取总边数
    public int getEsize() {
        return esize;
    }
 
    public Map<V, List<E>> getVectors() {
        return vectors;
    }
}

六、图的遍历(深度优先)

根据题目，我这里介绍深度优先遍历的整个过程与实现。当然还有广度优先遍历，会在后面的最短路径上深入介绍。

1、题目节点遍历展示

我们随便找出一个小题：

从C点开始，在C点结束，沿途最多可以有3个站点，符合该要求的线路有几条？在下面给出的示例数据中，共有2条符合线路：C-D-C (2 站)，C-E-B-C (3 站)

从上面的图，我们来看下整体深度遍历是如何进行的：

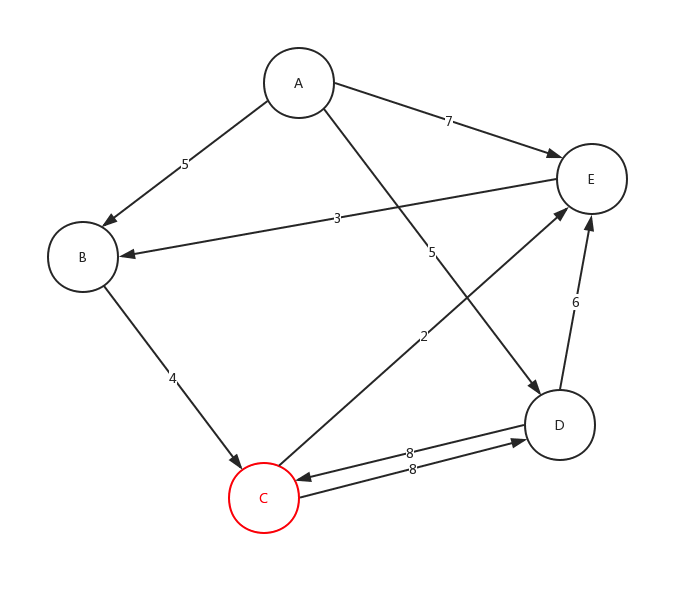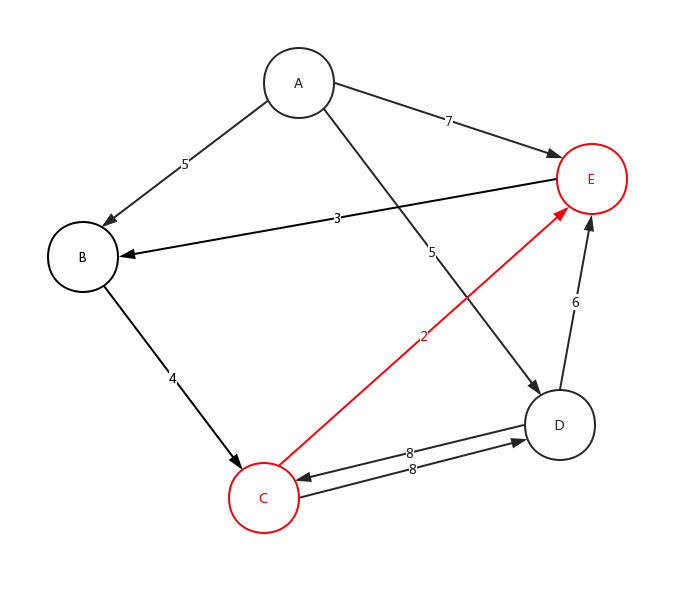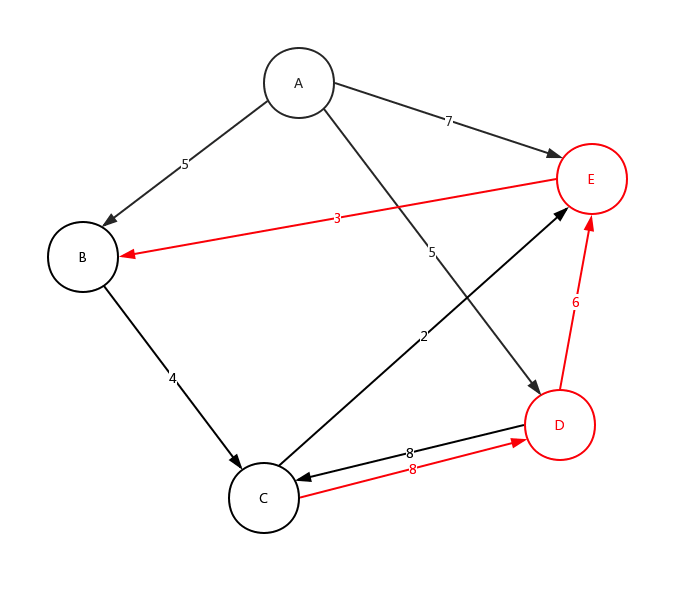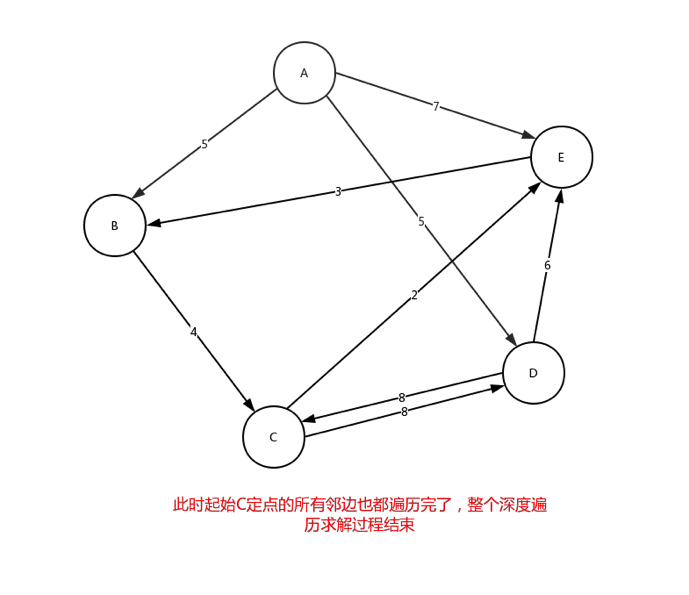
细心的看这个动态图，很好的展示了，整个深度遍历的求解过程。

2、代码实现

下面我就用代码来实现这一过程。相对来说，要实现这个过程并非那么容易，因为要控制类似于："最多"，"刚好"，"最多长度"等这些个区间求解。所以，要有响应的访问计数值，来进行辅助。首先我们来看看深度遍历图的对象的基础：


public class WordDepestPath {
 
    // 要遍历的图
    private Graph<WordVector, WordEdge> graph;
 
    // 记录当前边被访问到的次数
    private Map<WordEdge, Integer> edgeVisitedCount;
 
    // 记录当前顶点被访问到的次数
    private Map<WordVector, Integer> verticesVisitedCount;
 
    public WordDepestPath(Graph<WordVector, WordEdge> graph) {
        this.graph = graph;
        this.edgeVisitedCount = new HashMap<>();
        this.verticesVisitedCount = new HashMap<>();
 
        // 获取图的邻接表
        Map<WordVector, List<WordEdge>> vectors = graph.getVectors();
        // 遍历所有的边，进行初始化
        for (Map.Entry<WordVector, List<WordEdge>> entry : vectors.entrySet()) {
            List<WordEdge> value = entry.getValue();
            for (WordEdge it : value) {
                // 起始状态顶点和边都没有被访问到一次
                edgeVisitedCount.put(it, 0);
                verticesVisitedCount.put(it.getV1(), 0);
            }
        }
 
 
    }
}

这里的WordVector、WordEdge分别是IVertices、IEdge的实现，主要顶点内包装了个字符串，例如："A"。当然，因为要作为map的key值，必须要实现hashcode与equals方法，如下代码：


public class WordEdge implements IEdge<WordVector>, Comparable<WordEdge> {
 
    private WordVector v1, v2;
 
    private int weight;
 
    public WordEdge() {
    }
 
    public WordEdge(WordVector v1, WordVector v2, int weight) {
        this.v1 = v1;
        this.v2 = v2;
        this.weight = weight;
    }
 
    @Override
    public WordVector getV1() {
        return v1;
    }
 
    @Override
    public WordVector getV2() {
        return v2;
    }
 
    @Override
    public int getWeight() {
        return weight;
    }
 
    @Override
    public boolean equals(Object o) {
        if (this == o) return true;
        if (o == null || getClass() != o.getClass()) return false;
        WordEdge wordEdge = (WordEdge) o;
        return weight == wordEdge.weight &&
                Objects.equals(v1, wordEdge.v1) &&
                Objects.equals(v2, wordEdge.v2);
    }
 
    @Override
    public int hashCode() {
 
        return Objects.hash(v1, v2, weight);
    }
 
 
    @Override
    public String toString() {
        return "WordEdge{" +
                "v1=" + v1 +
                ", v2=" + v2 +
                ", weight=" + weight +
                '}';
    }
 
    @Override
    public int compareTo(WordEdge o) {
        return this.weight - o.getWeight();
    }
}
 
public class WordVector implements IVertices<String>, Comparable<WordVector>{
 
    private int index;
 
    private String word;
 
    public WordVector() {
    }
 
    public WordVector(int index, String word) {
        this.index = index;
        this.word = word;
    }
 
    @Override
    public int getIndex() {
        return index;
    }
 
 
    @Override
    public boolean equals(Object o) {
        if (this == o) return true;
        if (o == null || getClass() != o.getClass()) return false;
        WordVector that = (WordVector) o;
        return index == that.index &&
                Objects.equals(word, that.word);
    }
 
    @Override
    public int hashCode() {
 
        return Objects.hash(index, word);
    }
 
    @Override
    public String toString() {
        return word;
    }
 
    @Override
    public int compareTo(WordVector o) {
        return this.getIndex() - o.getIndex();
    }
 
    @Override
    public String getData() {
        return this.word;
    }
}

下面是深度遍历的入口方法：


		public List<List<WordEdge>> depestPath(WordVector src, WordVector dest) {
        List<List<WordEdge>> result = new ArrayList<>();
        Map<WordVector, List<WordEdge>> vectors = this.graph.getVectors();
        List<WordEdge> wordEdgesSrc = vectors.get(src);
        List<WordEdge> wordEdgesDest = vectors.get(dest);
        if (wordEdgesSrc == null || wordEdgesDest == null) {
            throw new IllegalArgumentException("没有此次搜索路径的结点");
        }
        for (WordEdge edge : wordEdgesSrc) {
            Stack<WordEdge> stack = new Stack<>();
            stack.push(edge);
            edgeVisitedCount.put(edge, edgeVisitedCount.get(edge) + 1);
            depestPathLargest3(edge, dest, 1, stack, result);
 
            edgeVisitedCount.put(stack.peek(), 0);
            stack.pop();
        }
 
        return result;
    }

最后是我们核心深度递归遍历图的方法：


		/**
     * 最多三站地的路径求解方法
     * 解决思路：
     * 如果整个路径上面最多只允许有三个顶点（除开起始节点）
     * 那么就是说，如果是一个有环有向图，那么这个解的边
     * 最多只能被访问一次。如果多被访问一次，那么就会超出
     * 三个顶点的题目要求，所以整个过程，重点要控制这个边
     * 的访问次数
     * @param currentEdge 当前遍历到的边
     * @param dest 目标顶点
     * @param largest 当前遍历到的站点的数量
     * @param stack 栈，用于辅助保存遍历节点
     * @param result 结果集，保存了所有符合条件的路径
     */
    private void depestPathLargest3(WordEdge currentEdge, WordVector dest, int largest,
                                    Stack<WordEdge> stack, List<List<WordEdge>> result) {
        // 递归终止条件
        if (edgeVisitedCount.get(stack.peek()).intValue() >= 2) {
            stack.pop();
            return;
        }
 
        WordVector v2 = currentEdge.getV2();
        // 注意这里：如果到了目的顶点，但是不满足最长路径值，同样不能成为结果
        if (v2.getData().equals(dest.getData()) && largest <= 3) {
            // 此分支，就是表示一条我们求解的路径
            ArrayList<WordEdge> rightPath = new ArrayList<>();
            result.add(rightPath);
            for (WordEdge it : stack) {
                rightPath.add(it);
            }
        }
 
        List<WordEdge> edges = this.graph.getVectors().get(v2);
 
        // 这种情况表示下个顶点没有临边，那就要栈顶的边不可走，要出栈
        if (edges.isEmpty()) {
            stack.pop();
            return;
        }
 
        // 对当前层遍历到的边的结束顶点，进行邻接边的遍历
        for (WordEdge it : edges) {
            // 每每遍历到了一个邻接边，要进行入栈+计数
            stack.push(it);
            edgeVisitedCount.put(it, edgeVisitedCount.get(it) + 1);
            // 开始递归
            depestPathLargest3(it, dest, largest + 1, stack, result);
        }
 
        /**
         *  注意这里，走到了这个地方，表示遍历邻边已经结束，
         *  每次弹出一个值的之前，要把这个邻边对应的访问计数
         *  清零，为了不影响后面的递归结束判断
         */
        edgeVisitedCount.put(stack.peek(), 0);
        stack.pop();
 
    }

根据这种思路，我们要求解下面两个问题，也是依葫芦画瓢了：

从A点开始，在C点结束，要求线路上必须有4个站点，符合该要求的线路有几条？在下面给出的示例数据中，共有3条符合线路：A 到 C (通过 B,C,D); A 到 C (经过 D,C,D); 以及 A 到 C (经过 D,E,B).
从C点开始，在C点结束，要求距离小于30，符合该要求的线路有几条？在下面给出的示例数据中，符合条件的线路有：CDC, CEBC, CEBCDC, CDCEBC, CDEBC, CEBCEBC, CEBCEBCEBC.

七、图的最短路径问题

我们这里求最短路径，使用最经典的迪杰克斯拉算法(Dijkstra)，这个算法，用来求单源最短路径使用，有一定的限制：

所有边的权值只能是正数，不能有负权边
每次要使用索引堆进行辅助

下面我们一步步来讲解下，如何求上面算法题中的一小题，就是最短路径的问题：

A 到 C的最短路线长度

1、迪杰克斯拉算法展示

下面是动图展示，然后我们一步步说如何求解：

一些前置条件：

索引堆中，索引值对应每个节点：1->A，2->B，3->C，4->D，5->E
索引堆中，具体的真实值存储选取的单源节点到当前节点最短的路径值：A->0，B->5，C->9，D->5，E->7

下面是具体的求解过程：

首先将原点加入到堆中，那原点对应的值是0
开始循环从堆中拿堆顶的数据，直到堆为空为止
每次拿到数据之后，遍历拿到的节点的所有邻边
拿到每个邻边的另一端的结点，判断这个节点是否被确定下来
如果没有确定下来，那就看当前从此路径过来的总路径，是否比当前节点的路径要短
如果短，则跟新当前节点的路径值，如果不短，则跳过
当然，这个结点有可能还没有统计过路径长度，路径为空，这种时候直接将节点，对应的路径值，压入索引堆中
如果当前节点已经是确定路径的结点了，那就跳过当前节点与邻边的遍历
注意：每次从堆顶拿到的，是最小的路径值，那这个路径对应另一端的节点就被确认下来，因为我们没有考虑负权边，所以不可能存在另外一个路径，到这个节点还要短，所以每次堆顶拿到的值，必须要被标记成已确定
如此遍历，直到堆为空的情况结束

这就是全过程，下面我们来看看代码实现

2、迪杰克斯拉算法的代码实现


public class Dijsktra {
 
    // 我们要求解的原图（邻接表存储）
    private Graph<WordVector, WordEdge> graph;
 
    // 索引小顶堆
    private IndexMinPriorityQueue<Integer> queue;
 
    // 保存每个节点是否被确认下来的映射，默认是false
    private Map<WordVector, Boolean> isMarked;
 
    // 保存源节点到每个节点的最小路径值
    private Number[] distTo;
 
    // 保存每个节点的最短路径是从那个邻边到达的
    private WordEdge[] from;
 
    public Number[] getDistTo() {
        return distTo;
    }
 
    public Dijsktra(Graph<WordVector, WordEdge> graph, WordVector src) {
        this.graph = graph;
        this.queue = new IndexMinPriorityQueue<>(graph.getVsize());
        this.isMarked = new HashMap<>();
        distTo = new Number[graph.getVsize()];
        from = new WordEdge[graph.getVsize()];
        // 默认将每个节点的确认映射，设置成false，就是都是未确认状态
        for (Map.Entry<WordVector, List<WordEdge>> entry : graph.getVectors().entrySet()) {
            WordVector key = entry.getKey();
            isMarked.put(key, false);
        }
        // 初始化最短路径保存数组，与最短路径的邻边数组
        for (int i = 0; i < graph.getVsize(); i++) {
            distTo[i] = 0.0;
            from[i] = null;
        }
 
        // 第一个将源节点加入到结构中
        from[src.getIndex()] = new WordEdge(src, src, 0);
        // 注意，加入的索引值与对应的结点，还有值是路径的长度
        this.queue.insert(src.getIndex(), from[src.getIndex()].getWeight());
        this.isMarked.put(src, true);
 
        // 开始遍历索引堆
        while (!this.queue.isEmpty()) {
            // 获取堆顶的元素索引
            Integer nodeIndex = this.queue.delElemetIndex();
            // 通过索引值与邻边数组，获取对应的当前遍历的堆顶定点
            WordVector v2 = from[nodeIndex].getV2();
            // 当前节点就是最短路径了，所以标记已被确认
            this.isMarked.put(v2, true);
            // 开始遍历当前节点的所有邻边
            List<WordEdge> edges = this.graph.getVectors().get(v2);
            for (WordEdge it : edges) {
                // 查询邻边另一边的结点，看看路径情况
                WordVector nextNode = it.getV2();
                if (!this.isMarked.get(nextNode)) {
                    int nextNodeIndex = nextNode.getIndex();
                    /**
                     *  核心：首先的if逻辑判断很关键，
                     *  看看当前节点索引对应的路径值有没有开始统计，
                     *  并且如果开始统计有值的话，就计算从当前邻边到
                     *  达当前节点的路径长度，是否小于已经存在的路径
                     *  如果小，就要更新，不小就略过。
                     */
                    if (from[nextNodeIndex] == null
                            || distTo[v2.getIndex()].intValue() 
                        + it.getWeight() < distTo[nextNodeIndex].intValue()) {
 
                        // 内部，表示要更新当前节点的最短路径，那就要改各个数组与索引堆中的值
                        distTo[nextNodeIndex] = distTo[v2.getIndex()].intValue() 
                          + it.getWeight();
                        from[nextNodeIndex] = it;
                        // 索引堆也有两种情况，有这个值，没这值
                        if (queue.contain(nextNodeIndex))
                            queue.change(nextNodeIndex,  distTo[nextNodeIndex].intValue());
                        else
                            queue.insert(nextNodeIndex, distTo[nextNodeIndex].intValue());
                    }
                }
            }
        }
 
    }
}

如此，其实已经解决了我们题目中的所有问题

转载于:https://my.oschina.net/UBW/blog/3039949

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/小舞很执着/article/detail/943796