Viterbi译码及其matlab和FPGA实现_matlab viterbi

Viterbi译码由美国科学家Viterbi在1967年提出¹,是卷积码的译码算法，是一种最大似然译码算法，其通过寻找距离最短的译码路径来实现。这篇文章侧重实现，具体原理就不说明了。

matlab实现Viterbi译码

卷积码

Viterbi译码是卷积码的译码方式，因此首先给出卷积码的matlab实现方式。

trellis= poly2trellis(7, [171 133]);
codeData = convenc(bits,trellis);
1
2

matlab官方给出的示例是：

trellis = poly2trellis(ConstraintLength,CodeGenerator) 
1

bits是编码前的数据。
poly2trellis生成一个结构体，其输入为(卷积码的级数，多项式的表达式)。如这个代码中卷积码的级数为7，多项式的表达式有两个，是八进制的表示，代表对应位置的抽头，如171位1111001，代表7级的数据是否要用于多项式的计算。
输出的值包含五个：
numInputSymbols: 输入状态数，输入bit^2
numOutputSymbols:输出状态数，输出bit^2
numStates:寄存器状态数，(级数-1)^2
nextStates:由当前状态和输入决定下一个状态
outputs:由当前状态和输入决定的输出
如代码中的卷积码：
numInputSymbols:2
numOutputSymbols:4
numStates:64
nextStates:64 * 2的数组
outputs:64 * 2的数组

viterbi译码

decodeData = vitdec(codeData ,trellis,42,'trunc','hard');
1

matlab官方给出的示例是：

decodedout = vitdec(codedin,trellis,tbdepth,opmode,dectype)
1

codedin:编码后的数据
trellis：前面poly2trellis生成的值
tbdepth:traceback depth，回溯深度
matlab官方对tbdepth给出的说明：As a general estimate, a typical traceback depth value is approximately two to three times (ConstraintLength – 1) / (1 – coderate). A rate 1/2 code has a traceback depth of 5(ConstraintLength – 1)… 即典型的回溯深度一般为(卷积码的级数-1)/(1-码率)，码率即为输入和输出的比例，对于本文的卷积码，一个输入二个输出，所以码率为1/2，即5*(7-1)是合理的值，即为30，这个值取大取小一点也没关系，这里取了42。
dectype:decoding type,有’unquant’，‘hard’，‘soft’三种。对于’hard’,解码器期望二进制输入值为 0 或 1。

FPGA实现Viterbi译码

卷积码

卷积码在FPGA实现十分容易，靠移位寄存器和异或运算即可实现：

//移位寄存器
reg [6:0] conv_reg;
always@(posedge sys_clk or negedge sys_rst_n)begin
    if(!sys_rst_n)
        conv_reg<='d0;
    else
        conv_reg<={din,conv_reg[6:1]};
end

//生成多项式
reg [1:0] dout_reg;
always@(posedge sys_clk or negedge sys_rst_n)begin
    if(!sys_rst_n)
        dout_reg<='d0;
    else begin
        dout_reg[1]<=conv_reg[0]^conv_reg[3]^conv_reg[4]^conv_reg[5]^conv_reg[6]; //171
        dout_reg[0]<=conv_reg[0]^conv_reg[1]^conv_reg[3]^conv_reg[4]^conv_reg[6]; //133
    end
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

根据171和133(八进制)的二进制表示，来写生成多项式。

Viterbi译码

Xilinx有IP可以使用。

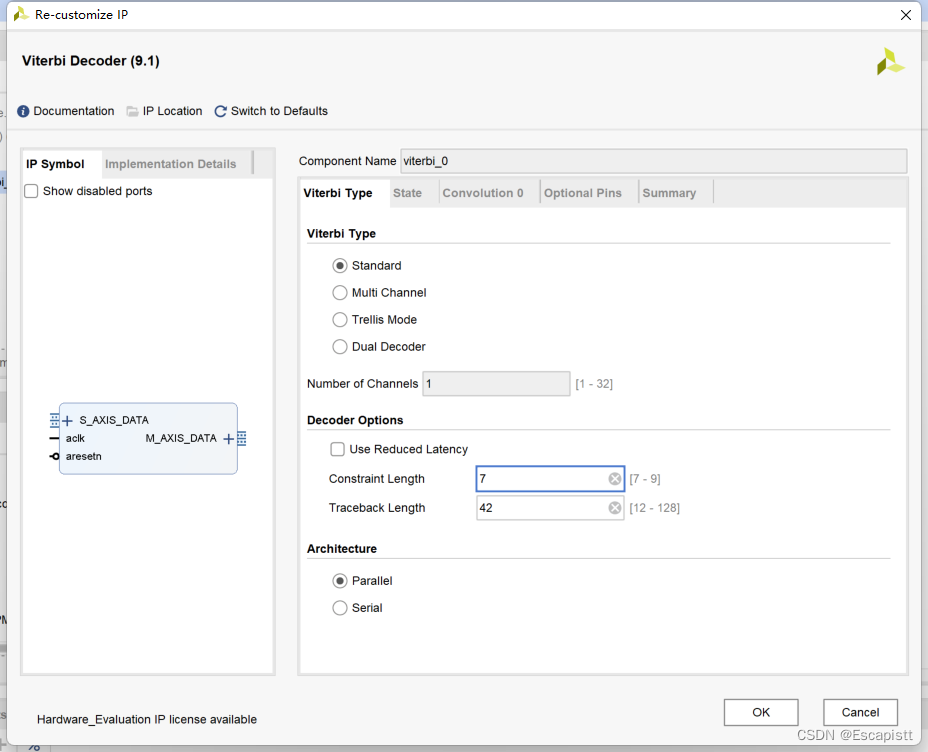
Viterbi Type配置constraint length，traceback length。

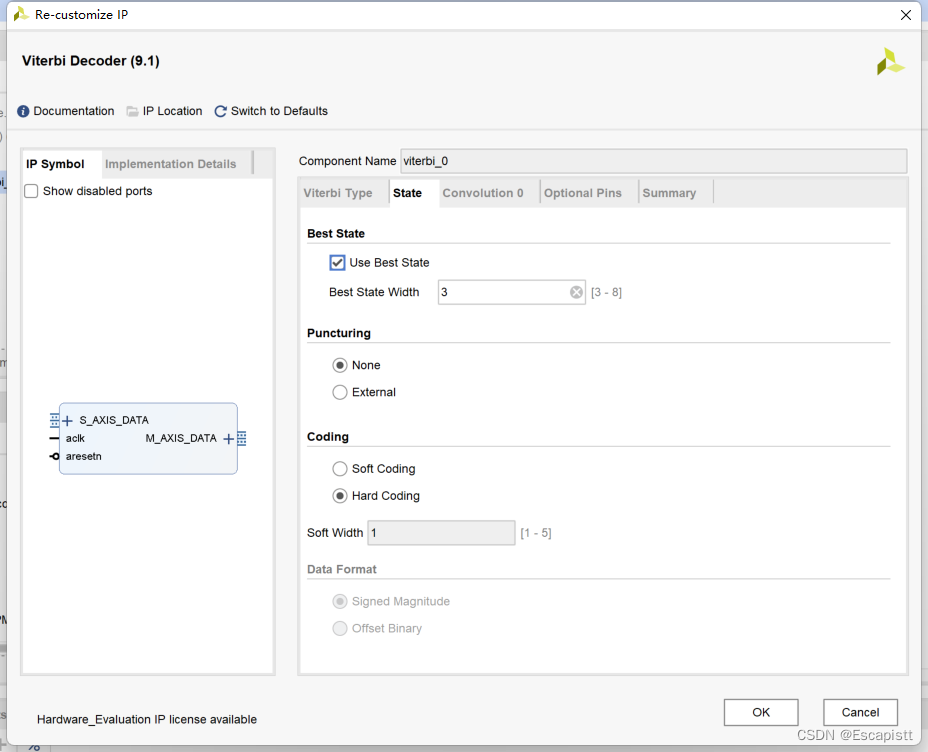
State配置hard coding

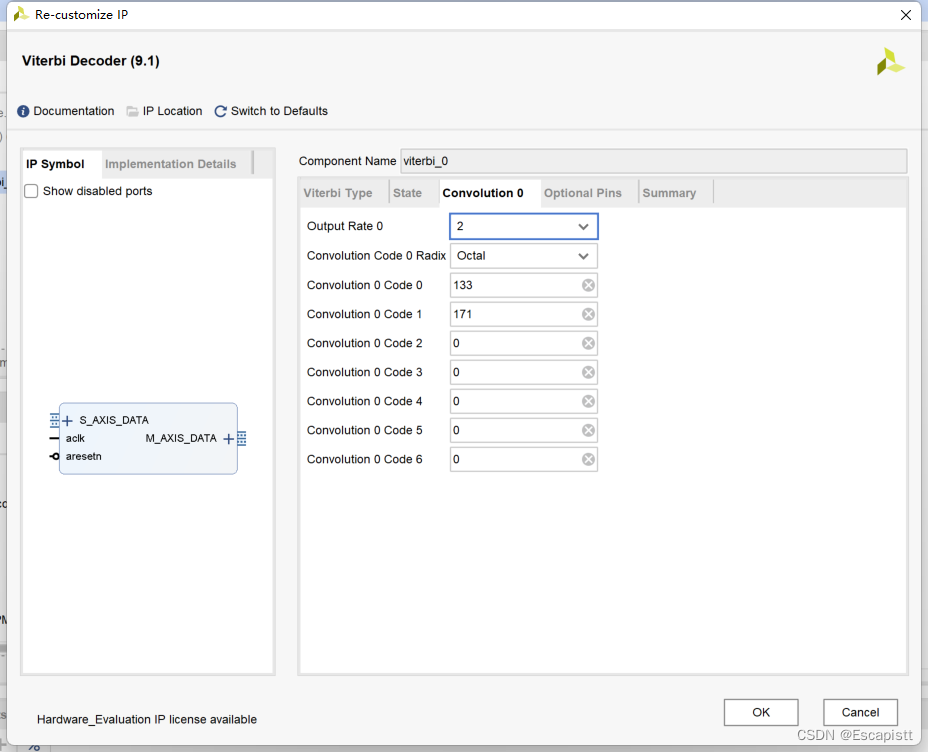
convolution 0配置生成多项式
这些配置与matlab设计一致。

---

1. FORNEY G D. The viterbi algorithm [J]. Proceedings of the IEEE, 1973, 61(3): 268-78. ↩︎