pagerank算法_PageRank 及衍生

PageRank

简介：是由Google创始人Larry Page 和 Sergey Brin受“论文的影响力”所提出，用于标识网页的重要性的方法，是Google用来衡量一个网站的好坏的唯一标准。在揉合了诸如Title标识和Keywords标识等所有其它因素之后，Google通过PageRank来调整结果，使那些更具“等级/重要性”的网页在搜索结果中另网站排名获得提升，从而提高搜索结果的相关性和质量。

相关概念：

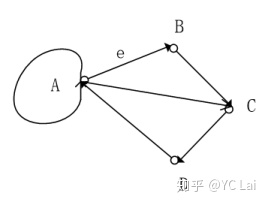
有向图：边（Edge）有方向的图，即 A➡️B != B➡️A

无向图：边没有方向的图。

入度：有向图某个点作为终点的次数之和

出度：有向图某个点作为起点的次数之和

度=入度+出度

上图中 A的出度=2，A的入度=1，度=3

PageRank两个假设：

• 数量假设：在Web图模型中，如果一个页面节点接收到的其他网页指向的入链数量越多，那么这个页面越重要。
• 质量假设：指向页面A的入链质量不同，质量高的页面会通过链接向其他页面传递更多的权重。所以越是质量高的页面指向页面A，则页面A越重要。

公式：

是待估计网页，

为

的入链集合，

是

页面的出链数量。即一个页面的得票数由所有链向它的页面的重要性来决定，到一个页面的超链接相当于对该页投一票。一个页面的PageRank是由所有链向它的页面（链入页面）的重要性经过递归算法得到的。

求解：

将上面一个公式转化为矩阵形式。首先需要写出转移矩阵，即网页对于其它页面的跳转概率。

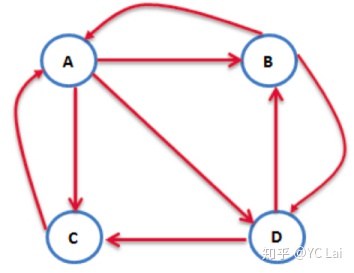
由上图可以写出转移矩阵：

每一列表示某个节点转移到其它节点的转移概率。

就是A转移到B的概率是1/3（下标从0开始），其实就是出链的概率。

步骤

首先假设每个节点的初始权重相等，然后通过不断地进行迭代得到稳定的权重。

经过一次迭代之后：

,

需要多次迭代才能最终稳定。

问题

因为节点有可能没有出度或者没有入度，最终这些会造成Rank Leak或者Rank Sink。

Rank Leak（等级泄露）：一个网页没有出链，就像是一个黑洞一样，吸收了别人的影响力而不释放，最终会导致其他网页的PR值为0。

Rank Sink（等级沉没）：一个网页只有出链，没有入链。比如节点A迭代下来，会导致这个网页的PR值为0。

解决方法：增加阻尼因子

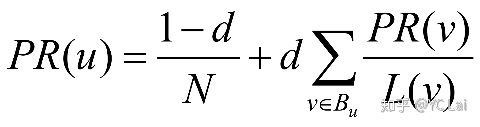
python代码：

def random_work(a, w, n):
	
    d = 0.85
	
    for i in range(100):
		
       w = (1-d)/n + d*np.dot(a, w)
		
       print(w)

也有现成的库可以使用：

import networkx as nx
import matplotlib.pyplot as plt
# 创建有向图
 
G = nx.DiGraph() 
# 有向图之间边的关系
edges = [("A", "B"), ("A", "C"), ("A", "D"), ("B", "A"), ("B", "D"), ("C", "A"), ("D", "B"), ("D", "C")]
for edge in edges:
    
    G.add_edge(edge[0], edge[1])
# 有向图可视化
layout = nx.spring_layout(G)
nx.draw(G, pos=layout, with_labels=True, hold=False)
plt.show()
pagerank_list = nx.pagerank(G, alpha=0.8)
print("pagerank值是：", pagerank_list)
#常用操作：
#添加节点：使用G.add_node('A')，也可以使用G.add_nodes_from(['B','C','D','E'])
#删除节点：使用G.remove_node(node)，也可以使用G.remove_nodes_from(['B','C','D','E'])
#边的增加
G.add_edge("A", "B")添加指定的从A到B的边
G.add_edges_from 
#从边集合中添加
G.add_weighted_edges_from 从带有权重的边的集合中添加
 
#边的删除
G.remove_edge，G.remove_edges_from
#边的查询
G.edges()获取图中所有边，G.number_of_edges()获取图中边的个数。

衍生思想：

将数据转化为图结构的形式，用来进行影响力的分析。

Ex：1. 推荐系统 2. 文章分析 3. 交通网络

TextRank：

用于分析文章，将词作为节点，词跟着词，就是节点连接节点，然后就构建了图结构。

• 如果一个单词出现在很多单词后面的话，那么说明这个单词比较重要
• 一个TextRank值很高的单词后面跟着的一个单词，那么这个单词的TextRank值会相应地因此而提高

例如：Compatibility of systems of linear constraints over the set of natural numbers. Criteria of compatibility of a system of linear Diophantine equations, strict inequations, and nonstrict inequations are considered. Upper bounds for components of a minimal set of solutions and algorithms of construction of minimal generating sets of solutions for all types of systems are given. These criteria and the corresponding algorithms for constructing a minimal supporting set of solutions can be used in solving all the considered types systems and systems of mixed types.

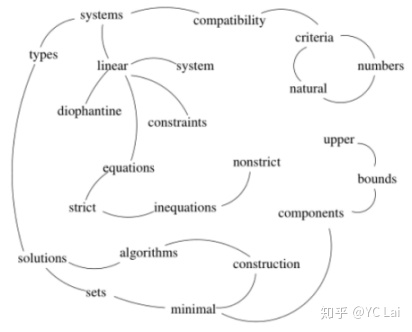
至于一些介词、量词、动词等都没有在上图显示，原因是因为提前选择了词性，再转换成图结构。

步骤：

1. 进行分词和词性标注，将单词添加到图中
2. 出现在一个窗口中的词形成一条边
3. 基于PageRank原理进行迭代（20-30次）
4. 顶点（词）按照分数进行排序，可以筛选指定的词性

from textrank4zh import TextRank4Keyword, TextRank4Sentence
import jieba
 
text = 'xxxxxxxxxxxxxxxxxxxxxxxxxxxx'
# 输出关键词，设置文本小写，窗口为2
tr4w = TextRank4Keyword()
tr4w.analyze(text=text, lower=True, window=3)
print('关键词：')
for item in tr4w.get_keywords(20, word_min_len=2):
    print(item.word, item.weight)
 
 
# 输出重要的句子
tr4s = TextRank4Sentence()
tr4s.analyze(text=text, lower=True, source = 'all_filters')
print('摘要：')
# 重要性较高的三个句子
for item in tr4s.get_key_sentences(num=3):
	# index是语句在文本中位置，weight表示权重
    print(item.index, item.weight, item.sentence

又一个现成的库textrank4zh可以使用。还有jieba库。

EdgeRank

用于分析信息流。利用用户之间的互动等行为结合内容质量来进行影响力分析。Facebook和微博都采用了这种方法，但好像并没有找到文章或者资料有写，比较隐秘。

• 当前用户与Edge创建者之间的亲密度
• Edge不同类型的权重，譬如创建、评论、点赞、打标签等
• Edge创建时间的时间衰减因素

Summary

其实都是从PageRank那里演变而来，应用于不同的场景。要想使用这类算法：

1. 需求：影响力排序，或者是相似度计算
2. 关联：将数据转化为 图结构

参考

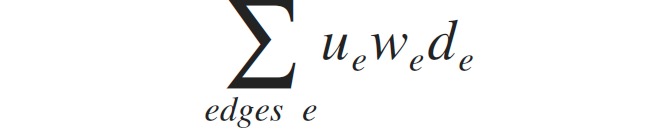
[1]. 陈旸老师的ppt。

[2]. PageRank原文