devbox
小桥流水78
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

经典算法题总结：二叉树篇

作者：小桥流水78 | 2024-08-15 03:26:13

赞

踩

经典算法题总结：二叉树篇

二叉树解题的思维模式分两类：

  1. 是否可以通过遍历一遍二叉树得到答案？如果可以，用一个 traverse 函数配合外部变量来实现，这叫「遍历」的思维模式。
  2. 是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。

无论使用哪种思维模式，你都需要思考：如果单独抽出一个二叉树节点，它需要做什么事情？需要在什么时候（前/中/后序位置）做？其他的节点不用你操心，递归函数会帮你在所有节点上执行相同的操作。

二叉树数据结构定义：

  1. public class TreeNode {
  2.     int val;
  3.     TreeNode left;
  4.     TreeNode right;
  5.  
  6.     public TreeNode() {
  7.     }
  8.  
  9.     public TreeNode(int val) {
  10.         this.val = val;
  11.     }
  12.  
  13.     public TreeNode(int val, TreeNode left, TreeNode right) {
  14.         this.val = val;
  15.         this.left = left;
  16.         this.right = right;
  17.     }
  18. }

102. 二叉树的层序遍历（⭐️⭐️）

思路

代码

  1. public class LevelOrder {
  2.  
  3.     public List<List<Integer>> levelOrder(TreeNode root) {
  4.         List<List<Integer>> res = new ArrayList<>();
  5.         Queue<TreeNode> queue = new LinkedList<>();
  6.         if (root != null) {
  7.             queue.add(root);
  8.         }
  9.         while (!queue.isEmpty()) {
  10.             int n = queue.size();
  11.             List<Integer> level = new ArrayList<>();
  12.             for (int i = 0; i < n; i++) {
  13.                 TreeNode node = queue.poll();
  14.                 level.add(node.val);
  15.                 if (node.left != null) {
  16.                     queue.add(node.left);
  17.                 }
  18.                 if (node.right != null) {
  19.                     queue.add(node.right);
  20.                 }
  21.             }
  22.             res.add(level);
  23.         }
  24.         return res;
  25.     }
  26.  
  27. }

复杂度

  • 时间复杂度：O(N)
  • 空间复杂度：O(N)

236. 二叉树的最近公共祖先（⭐️⭐️）

思路

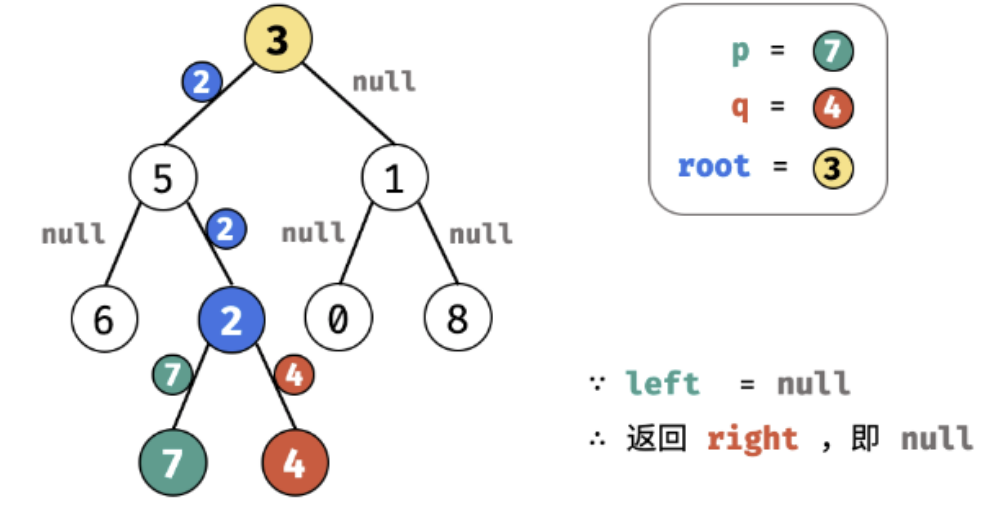
代码

  1. public class LowestCommonAncestor {
  2.  
  3.     public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
  4.         if (root == null || root == p || root == q) {
  5.             return root;
  6.         }
  7.         TreeNode left = lowestCommonAncestor(root.left, p, q);
  8.         TreeNode right = lowestCommonAncestor(root.right, p, q);
  9.  
  10.         if (left == null && right == null) {
  11.             return null;
  12.         } else if (left == null && right != null) {
  13.             return right;
  14.         } else if (left != null && right == null) {
  15.             return left;
  16.         } else {
  17.             return root;
  18.         }
  19.     }
  20.  
  21. }

复杂度

  • 时间复杂度：O(N)
  • 空间复杂度：O(log(N))

103. 二叉树的锯齿形层序遍历（⭐️⭐）

思路

代码

  1. import java.util.LinkedList;
  2. import java.util.List;
  3. import java.util.Queue;
  4.  
  5. public class ZigzagLevelOrder {
  6.  
  7.     public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
  8.         List<List<Integer>> res = new LinkedList<>();
  9.         if (root == null) {
  10.             return res;
  11.         }
  12.         Queue<TreeNode> queue = new LinkedList<>();
  13.         queue.offer(root);
  14.         boolean flag = true; // 为 true 时从右边开始遍历，false 时从左边开始
  15.         while (!queue.isEmpty()) {
  16.             int size = queue.size();
  17.             LinkedList<Integer> level = new LinkedList<>();
  18.             for (int i = 0; i < size; i++) {
  19.                 TreeNode node = queue.poll();
  20.                 if (flag) {
  21.                     level.addLast(node.val);
  22.                 } else {
  23.                     level.addFirst(node.val);
  24.                 }
  25.                 if (node.left != null) {
  26.                     queue.offer(node.left);
  27.                 }
  28.                 if (node.right != null) {
  29.                     queue.offer(node.right);
  30.                 }
  31.             }
  32.             flag = !flag;
  33.             res.add(level);
  34.         }
  35.         return res;
  36.     }
  37.  
  38. }

复杂度

  • 时间复杂度：O(N)
  • 空间复杂度：O(N)

124. 二叉树中的最大路径和（⭐️⭐️）

思路

代码

  1. class Solution {
  2.     int res = Integer.MIN_VALUE;
  3.  
  4.     public int maxPathSum(TreeNode root) {
  5.         traverse(root);
  6.         return res;
  7.     }
  8.  
  9.     // 返回当前节点能为父亲提供的贡献
  10.     private int traverse(TreeNode root) {
  11.         if (root == null) {
  12.             return 0;
  13.         }
  14.  
  15.         int left = traverse(root.left);
  16.         int right = traverse(root.right);
  17.         res = Math.max(res, root.val + left + right);
  18.         int max = Math.max(root.val + left, root.val + right); // 计算当前节点能为父亲提供的最大贡献
  19.         return max < 0 ? 0 : max;
  20.     }
  21.  
  22. }

复杂度

  • 时间复杂度：O(N)
  • 空间复杂度：O(log(N))

94. 二叉树的中序遍历（⭐️⭐️）

思路

中序遍历的过程中收集节点的值。

代码

  1. import java.util.ArrayList;
  2. import java.util.List;
  3.  
  4. public class InorderTraversal {
  5.  
  6.     public List<Integer> inorderTraversal(TreeNode root) {
  7.         List<Integer> list = new ArrayList<>();
  8.         traverse(root, list);
  9.         return list;
  10.     }
  11.  
  12.     private void traverse(TreeNode root, List list) {
  13.         if (root == null) {
  14.             traverse(root.left, list);
  15.             list.add(root.val);
  16.             traverse(root.right, list);
  17.         }
  18.     }
  19.  
  20. }

复杂度

  • 时间复杂度：O(N)
  • 空间复杂度：O(N)

199. 二叉树的右视图（⭐️⭐️）

思路

BFS每一层最后一个元素 or DFS 先访问每一层的右边的元素。

代码

  1. import java.util.ArrayList;
  2. import java.util.LinkedList;
  3. import java.util.List;
  4. import java.util.Queue;
  5.  
  6. public class RightSideView {
  7.     private List<Integer> res = new ArrayList<>();
  8.  
  9.     public List<Integer> rightSideViewBFS(TreeNode root) {
  10.         List<Integer> res = new ArrayList<>();
  11.         if (root == null) {
  12.             return res;
  13.         }
  14.         Queue<TreeNode> queue = new LinkedList<>();
  15.         queue.offer(root);
  16.         while (!queue.isEmpty()) {
  17.             int size = queue.size();
  18.             for (int i = 0; i < size; i++) {
  19.                 TreeNode node = queue.poll();
  20.                 if (node.left != null) {
  21.                     queue.offer(node.left);
  22.                 }
  23.                 if (node.right != null) {
  24.                     queue.offer(node.right);
  25.                 }
  26.                 if (i == size - 1) {
  27.                     res.add(node.val);
  28.                 }
  29.             }
  30.         }
  31.         return res;
  32.     }
  33.  
  34.     public List<Integer> rightSideViewDFS(TreeNode root) {
  35.         DFS(root, 0);
  36.         return res;
  37.     }
  38.  
  39.     private void DFS(TreeNode root, int depth) {
  40.         if (root == null) {
  41.             return;
  42.         }
  43.         if (depth == res.size()) {
  44.             res.add(root.val);
  45.         }
  46.         depth++;
  47.         DFS(root.right, depth);
  48.         DFS(root.left, depth);
  49.     }
  50.  
  51. }

复杂度

  • 时间复杂度：O(N)
  • 空间复杂度：方法一：O(N)，方法二：O(log(N))

105. 从前序与中序遍历序列构造二叉树（⭐️⭐️）

思路

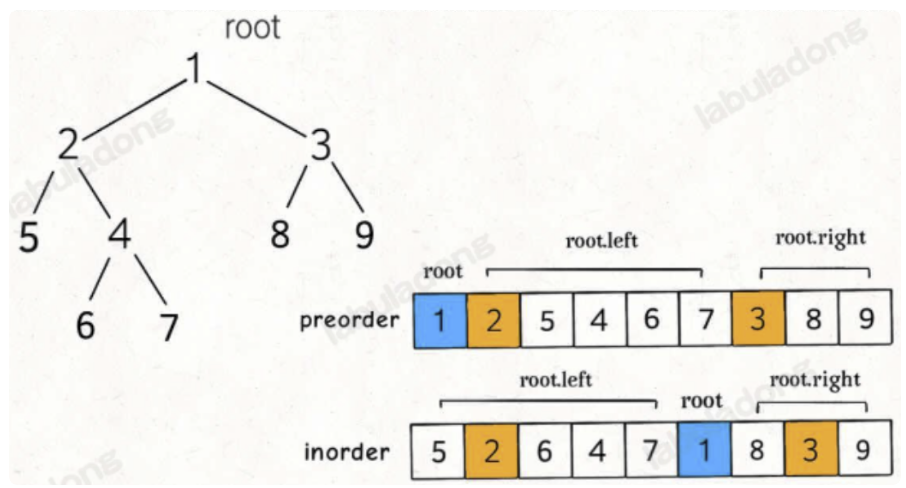
代码

  1. import java.util.HashMap;
  2. import java.util.Map;
  3.  
  4. public class BuildTree {
  5.     private Map<Integer, Integer> map = new HashMap<>();
  6.  
  7.     public TreeNode buildTree(int[] preorder, int[] inorder) {
  8.         for (int i = 0; i < inorder.length; i++) {
  9.             map.put(inorder[i], i); // 记录中序序列每一个值的位置，用来划分左右子树的节点数量
  10.         }
  11.         return traverse(preorder, 0, preorder.length - 1,
  12.                 inorder, 0, inorder.length - 1);
  13.     }
  14.  
  15.     private TreeNode traverse(int[] preorder, int preorderLeft, int preorderRight,
  16.                               int[] inorder, int inorderLeft, int inorderRight) {
  17.         if (preorderLeft > preorderRight || inorderLeft > inorderRight) {
  18.             return null;
  19.         }
  20.         int rootInInorderLocation = map.get(preorder[preorderLeft]);
  21.         int sizeLeftSubtree = rootInInorderLocation - inorderLeft;
  22.         TreeNode root = new TreeNode(preorder[preorderLeft]);
  23.         root.left = traverse(preorder, preorderLeft + 1, preorderLeft + sizeLeftSubtree,
  24.                 inorder, inorderLeft, rootInInorderLocation - 1);
  25.         root.right = traverse(preorder, preorderLeft + sizeLeftSubtree + 1, preorderRight,
  26.                 inorder, rootInInorderLocation + 1, inorderRight);
  27.         return root;
  28.     }
  29.  
  30. }

复杂度

  • 时间复杂度：O(N)
  • 空间复杂度：O(log(N))

129. 求根节点到叶节点数字之和（⭐️⭐）

思路

DFS

代码

  1. public class SumNumbers {
  2.  
  3.     public int sumNumbers(TreeNode root) {
  4.         return DFS(root, 0);
  5.     }
  6.  
  7.     private int DFS(TreeNode root, int preSum) {
  8.         if (root == null) {
  9.             return 0;
  10.         }
  11.         int sum = preSum * 10 + root.val;
  12.         if (root.left == null && root.right == null) {
  13.             return sum;
  14.         } else {
  15.             return DFS(root.left, sum) + DFS(root.right, sum);
  16.         }
  17.     }
  18.  
  19. }

复杂度

  • 时间复杂度：O(N)
  • 空间复杂度：O(N)

104. 二叉树的最大深度（⭐️⭐️）

思路

后序遍历更新当前节点左右子树的最大深度。

代码

  1. class Solution {
  2.  
  3.     public int maxDepth(TreeNode root) {
  4.         if (root == null) {
  5.             return 0;
  6.         }
  7.  
  8.         int leftHeight = maxDepth(root.left);
  9.         int rightHeight = maxDepth(root.right);
  10.         return Math.max(leftHeight, rightHeight) + 1;
  11.     }
  12.  
  13. }

复杂度

  • 时间复杂度：O(N)
  • 空间复杂度：O(log(N))
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/小桥流水78/article/detail/981810
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号