通俗易懂的KMP算法详解（严蔚敏版C语言）

    最近，需要复习KMP算法的next数组，然后回头看半年多后的我回头看半年多前自己综合别人内容写的介绍。     没错，自己也看不懂。然后，自己再根据自己的理解写了一下理解透彻的笔记，方便理解记忆，当然，以前的代码解释部分可以参考，笔记算法思维和算法的实现有一定的出入。望君谅解。（2018.9.30）

      

                                                                            

                                                                           这是一条时间分割线

_____________________________________________________________________________________________________

   

    从刚接触算法，感觉是跟不上的一片片片段，再往后自己看书理解，片段更是碎成一点点乱码。在下愚钝，在查询多种博客，结合书上（严蔚敏的数据结构）解释和代码，询问教师，后终于开窍。在此处引用了阮先生的部分思想，来通俗的讲解一下KMP算法。

   KMP算法与BF算法的根本区别

     解读KMP之前，我们先来理解一下KMP算法存在的理由。对于模式匹配，目前所学的最简单的是BF算法，即偏向于“暴力”匹配的方法。另外一种就是较为复杂KMP算法了。而俩者的区别在于：BF算法是时间复杂度相对高的，KMP则可以理解为用空间换时间。

     BF算法：        逐个匹配主串字符，然后模式串j值回溯到1重新匹配。

     KMP算法：       KMP只需要将j值模式串中j的位置回溯到next[j]位，而免除了前面不需要的匹配，以此来换取时间。

图片：

 相比一个一个比较，同学们肯定会更加想询问为什么不直接从模式串第一个字符和主串相同字符的位置比较即：       

图片：

     而KMP则在此基础上更加的简便了。

      接下来，我们来用有逻辑的语言来了解KMP算法。而后，再解释如何用代码实现该算法。

     首先，我们从代码的实现效果来看，主串与模式串每次历往KMP算法，模式串中移动至K位与失配的（主串）的i位对其，而不需要像BF算法一样，一次次回溯从头开始。

     那么，问题来了。K为何物？

     在此之前，我们来介绍一下最长前缀和最长后缀，和部分匹配。

     移动位数 =  已匹配值   -    部分匹配值     (其实就是直接从最长前缀直接跳到与他相等的最长后缀那里开始往后匹配）

上面都可以不用看

    效果大概是这样子：

以模式串ABCDABD,文本串BBCABCDABABCDABCDABDE为例子展示最大公共元素长度（最长前缀和他相等的最长后缀）。

     再来一遍：移动位数 =  已匹配值   -    最大公共元素长度

关键是计算next数组的值。

计算next数组的值，伪代码如下：

void get_next(SString T, int[] next){
     /*求模式串T的next函数值并存入数组next*/
       i=1; next[1]=0; j=0;
       while(i<T.length)
        {
          if(j==0||T.ch[i]==T.ch[j])
            {
                ++i;++j;             //相符合，前缀位数和后缀位数后退
                next[i]=j;
            }else{
                 j=next[j];    //前n位前缀不符合后n位后缀，使i待定，往前一位退，探测n-1位前缀和后缀是否符合
                 /**如果一直不符合，那么将一直退到0，进入if语句，i++下一位探测**/
            }
        
       }
}

解释next数组代码运算过程：

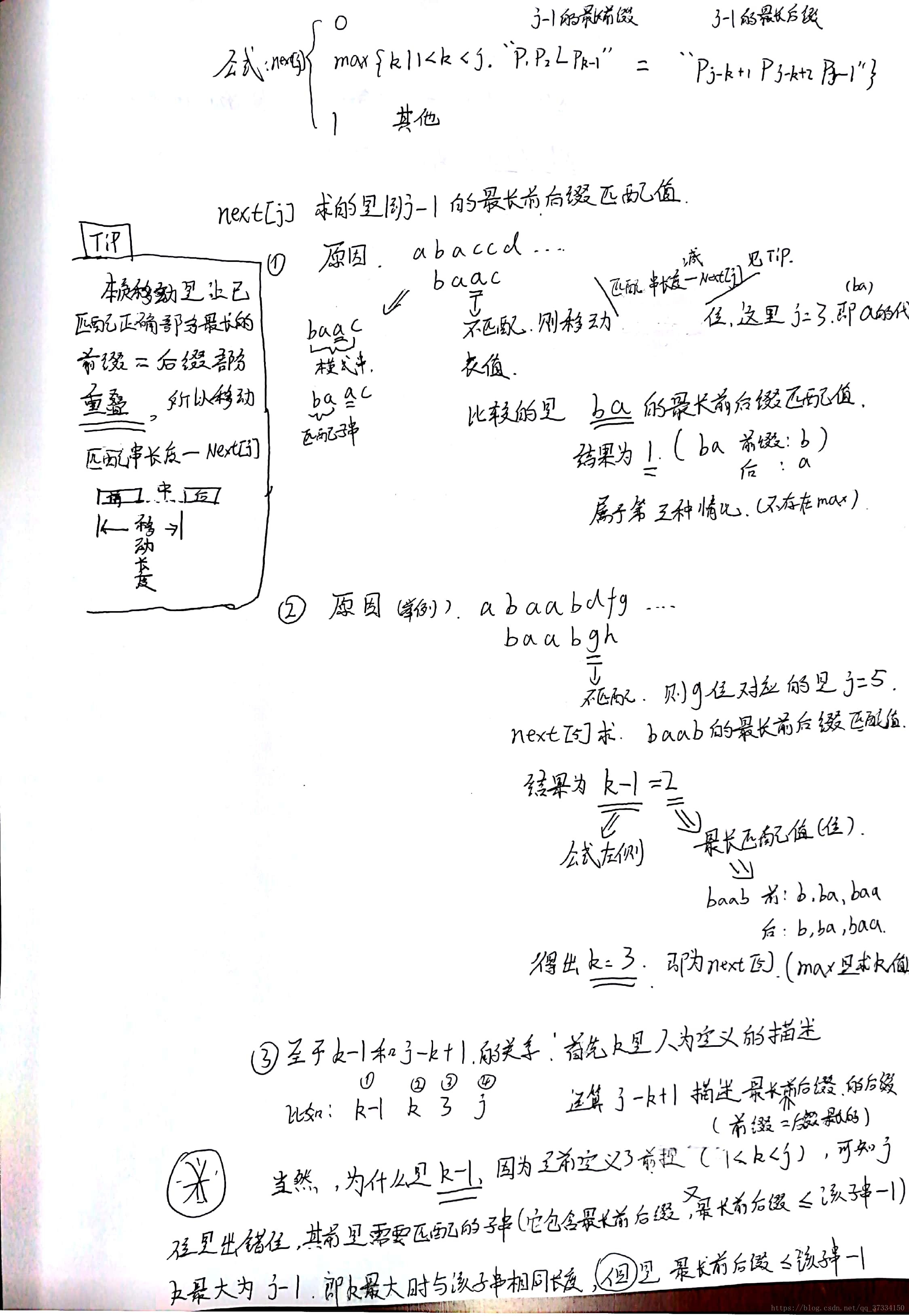
       next数组next[1]、next[2]固定为0，1，除next后还有next修正值,这里不讲。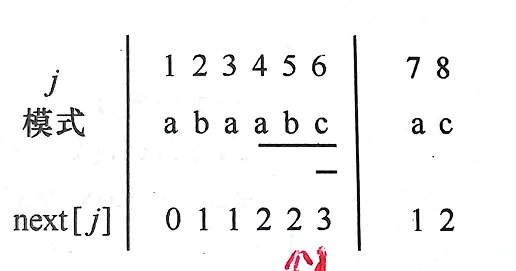

       以abaabc为例子(前面俩步自己按代码思维过一遍)： 第一个j=1（a）,i=3（a） 

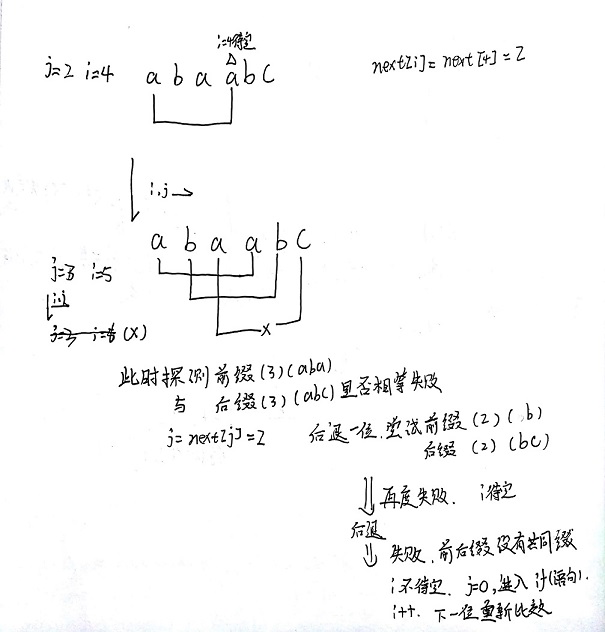
     ps:总之就是，先从第一个跟第二个比较，若成功就右滑比较，假设比较到三位连续相等：最大公共元素长度为3，第四位不等。  因为新增一个比较位，后缀的开头第一个改变需要重新比较（abc——>后缀：cba,;    abcd——>后缀：dcba），j回退一位，比较最大公共元素长度为3是否相等，不等继续后退减一（i一直为改变）。直到j=0，进入if语句，i++，下一个比较。计算next值的过程实质是计算模式串各个子串的最大公共元素长度。详细见最大公共元素长度效果图。然后方便模式串匹配文本串的时候，模式串直接从最长前缀直接跳到与他相等的最长后缀那里开始往后匹配。

下面是kmp的伪代码：

  

int index_KMP(SString S ,SString T, int[] next){//S为文本串，T为模式串
   while(i<=S.length && j<=T.length){
    
    if(j==0 || S.char[i]==T.char[j]){
            j++;i++;            //后一位是否连续性匹配
   }else j=next[j];            //从模式串的第j位开始和后面匹配，就是直接从最长前缀直接跳到与他相等的最长后缀那里
   
   if(j>T.length)
   {
       return i-T.length;   //匹配成功
   }else{
    return 0;             //匹配失败
   }
 
 
}