softmax交叉熵的两种形式 + numpy 实现_numpy softmax

交叉熵是用来描述两个分布的距离的

交叉熵定义：

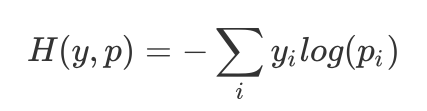
其中y代表我们的真实值，y是one-hot向量标签 ，pi代表我们softmax求出的值， p 向量的和是1。i 代表的是输出结点的标号。

多分类问题的交叉熵 

多分类交叉熵对应的最后一层是softmax，输出概率 p 的和为1。对应标签 y 是 one-hot向量。并且，y 中只有正确解标签的索引为1，其他均为0（one-hot表示）。实际上只计算对应正确解标签的输出的自然对数

  

二分类问题的交叉熵

再来看sigmoid作为最后一层的情况，sigmoid是一个二分类输出。sigmoid作为最后一层输出的话，那就不能把最后一层的输出看作成一个分布了，因为加起来不为1。现在应该将最后一层的每个神经元看作一个分布，对应的 target 属于二项分布(target的值代表是这个类的概率)。

在二分类问题中，y是真实的标签，其取值只可能为集合{0, 1}。模型最后需要预测的结果只有两种情况，对于每个类别我们的预测得到的概率为 p 和 1 - p ，此时表达式为

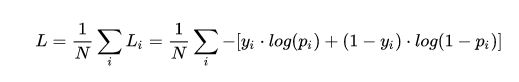
 - yi —— 表示样本 i 的label，正类为 1，负类为0
- pi —— 表示样本 i 预测为正类的概率

对于整个模型而言，其损失函数就是所有样本点的损失函数的平均值 

Python 代码实现：

均方误差numpy实现：

import numpy as np
def MSE(y,t):
    #形参t代表训练数据（监督数据）（真实）
    #y代表预测数据
    return 0.5*np.sum((y-t)**2)
 
 
# 设“2”为正确解
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
#假设预测下标为2是正确的
y1 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
print(MSE(np.array(y1),np.array(t)))
#输出：    0.09750000000000003，很小，代表误差很小，预测大概对了
 
#假设预测下标为7是正确的
y2 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
print(MSE(np.array(y2),np.array(t)))
#输出：    0.5975   ，很大，代表误差大，表示预测很不好

softmax + 交叉熵 代码实现

Softmax 可以将全连接层的输出映射成一个概率的分布，我们训练的目标就是让属于第k类的样本经过 Softmax 以后，第 k 类的概率越大越好。

# numpy定义softmax函数
def softmax(x):
	exps = np.exp(x) 
    return exps / np.sum(exps)

需要注意的是，在 numpy 中浮点类型是有数值上的限制的。对于指数函数来说，这个上限很容易就会被打破，如果这种情况发生了 python 便会返回 nan。
为了让 Softmax 函数在数值计算层面更加稳定，避免它的输出出现 nan 这种情况，一个很简单的方法就是对输入向量做一步归一化操作，仅仅需要在分子和分母上同乘一个常数 C(比如小于1的数，让输出变小)，理论上来说，我们可以选择任意一个值作为，但是一般我们会选择 输入数值的最大值，避免出现nan的情况。

同样使用 Python，改进以后的 Softmax 函数可以这样写：

def softmax(x):
    exps = np.exp(x - np.max(x)) 
    return exps / np.sum(exps)

交叉熵代码：

def sigmoid(x):
    return (1/(1+np.exp(x)))
 
def softmax(x):
	exps = np.exp(x - np.max(x)) 
    return exps / np.sum(exps)
	
def cross_entropy_error(p,y):
    assert y.shape == y_hat.shape
    delta=1e-7       #添加一个微小值可以防止负无限大(np.log(0))的发生。
	p = softmax(p)   # 通过 softmax 变为概率分布，并且sum(p) = 1
    return -np.sum(y*np.log(p+delta))
 
 
# label 标签都是 one-hot形式， 只有正确解标签的索引为1，其他均为0
 
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y1 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
print(cross_entropy_error(np.array(y1),np.array(t)))  #输出0.510825457099338（也比较小啦）
 
y2 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
print(cross_entropy_error(np.array(y2),np.array(t)))  #2.302584092994546

Pytoch 代码实现：

y = torch.Tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]])
# softmax
soft_y = torch.nn.Softmax(dim=-1)(y)
print("step1:softmax result=")
print(soft_y)
 
log_soft_y=torch.log(soft_y)
print('log soft y:')
print(log_soft_y)
 
# label  y_  one-hot 形式
y_ = torch.Tensor([[0.0, 0.0, 1.0], [0.0, 0.0, 1.0], [0.0, 0.0, 1.0]])
 
ce=-torch.mean(y_*log_soft_y)
print('tf way ce: ', ce)
y_2 = torch.LongTensor([2, 2, 2])
ce_torch=torch.nn.NLLLoss()(log_soft_y,y_2)
print('torch way ce :',ce_torch)

调用Pytoch 中的现有函数：

nn.CrossEntropyLoss()这个损失函数用于多分类问题虽然说的是交叉熵，但是和我理解的交叉熵不一样。nn.CrossEntropyLoss()是nn.logSoftmax()和nn.NLLLoss()的整合,可以直接使用它来替换网络中的这两个操作

实现方式1：

criterion=nn.CrossEntropyLoss()
loss=criterion(input,target)

实现方式2：

nn.logSoftmax()和nn.NLLLoss()讲解：

1、nn.logSoftmax()：使用softmax将预测转化为概率，然后对概率值取对数（等价于torch.nn.Softmax() + torch.log()）

2、nn.NLLLoss()：NLLLoss结果就是把上面取对数之后的结果与Label对应的那个值拿出来，再去掉负号，然后求和取均值。

# 对输出值进行计算softmax，并取对数,
# 而这个output是需要在神经网络模型的输出return语句当中就要计算好的
output=F.log_softmax(x,dim=-1)
# 使用pytorch当中的带权损失
loss=F.nll_loss(output,target)

概念讲解

官方例子：

m = nn.LogSoftmax(dim=1)
loss = nn.NLLLoss()
input = torch.randn(3, 5, requires_grad=True) # input is of size N x C = 3 x 5
target = torch.tensor([1, 0, 4]) # each element in target has to have 0 <= value < C,y是类别标签(不在是softmax输出的向量)
output = loss(m(input), target)

Softmax和交叉熵的深度解析和Python实现 

多分类的交叉熵和二分类的交叉熵有什么联系？

两种交叉熵损失函数的异同

PYTHON(NUMPY)实现均方差、交叉熵损失函数等