第十四届蓝桥杯C++B组编程题题目以及题解_2024蓝桥杯答案

a.冶炼金属（二分）

思路：

设任意一条冶炼记录投入金属数量为a,产出金属为b.

对于每一条冶炼记录我们都可以得到 一个转换率V的范围：

b<=a/v<b+1即a/b<= v <a/(b+1)

为什么是b+1呢？因为既然能产出b个金属，也就意味着一定不能产出b+1个，所以a/v<b+1

每一条记录都可以得到v的一个区间，我们不断地取交集，可以得到v的可能的最大值max和可能的最小值min。

在这里要注意，得到的max和minb并不就是答案，而是要在这个区间筛选出符合所有冶炼记录的v,再在这些v里面取最大值和最小值就是答案。这一步可以用二分。

代码：

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e4 + 10;
int arr[N][2];//冶炼金属的记录
 
int main() {
    int t;
    cin >> t;
    int maxv = 1e9;
    int minv = 0;
    for (int i = 0; i < t; i++) {
        int a, b;
        cin >> a >> b;
        arr[i][0] = a;
        arr[i][1] = b;
        maxv = min(maxv, a / b);//区间取交集，右端点要不断地取最小值，
        minv = max(minv, (a) / (b + 1));//区间取交集，左端点要不断地取最大值，
    }
 
    //两次二分分别得到最大值和最小值
    int l = minv;
    int r = maxv + 1;
    int ans1 = 0, ans2 = 0;
    while (l + 1 != r) {
        int mid = (l + r) >> 1;
        int f = 0;
 
        for (int i = 0; i < t; i++) {
            if (arr[i][0] / mid != arr[i][1]) {
                f = 1;
                break;
            }
        }
        if (f) {
            l = mid;
        }
        else r = mid;
    }
    ans1 = r;
    l = minv;
    r = maxv + 1;
    //int ans1=0,ans2=0;
    while (l + 1 != r) {
        int mid = (l + r) >> 1;
        int f = 0;
 
        for (int i = 0; i < t; i++) {
            if (arr[i][0] / mid != arr[i][1]) {
                f = 1;
                break;
            }
        }
        if (f) {
            r = mid;
        }
        else l = mid;
    }
    ans2 = l;
    cout << ans1 << " " << ans2 << endl;
 
    return 0;
}

b.飞机降落（dfs）

思路：

这题就是求能否存在一个飞机降落的顺序序列，能没有冲突的降落。这里的没有冲突是指，在当前时刻t<=当前飞机的最迟起飞时间（Ti+Di）.

由于题目数据很小，飞机的数量最多10，我们可以暴力枚举飞机所有的的降落顺序，再检查是否存在某一个顺序可以让全部飞机降落。

跟枚举全排列的思路是一样的，求一个长度为n且符合要求的飞机序号排列。对于当前的时间t,能不能让序号为u的飞机起飞，如果能则安排这台飞机降落，往下遍历时长度加一，如果不能，则说明这一条排列不行，就不安排这一台飞机，换台飞机试试。反正暴力么，所有情况都不重不漏。

代码：

 
#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 15;
int st[N];//标记已经降落的飞机
int a[N][3];//记录每一台飞机的起飞时间、盘旋时间、降落时间
int n;
bool ans;//标记答案
void dfs(int u, int t) {
    if (u == n) {//遍历到这里，长度已经够了，说明已经存在一个序列符合答案
        ans = true;
        return;
    }
    //安排下一台飞机
    for (int i = 1; i <= n; i++) {
        if (t > a[i][0] + a[i][1])continue;//不符合要求
        if (!st[i] && t <= a[i][0] + a[i][1]) {
            st[i] = 1;//标记序号为i的飞机要降落
            if (t <= a[i][0])dfs(u + 1, a[i][0] + a[i][2]);//如果当前的t比最早的起飞时间还早，那就等到时间为a[i][0]再降落
            else dfs(u + 1, t + a[i][2]);//否则就马上降落，更新时间
            st[i] = 0;//回溯
        }
    }
}
int main() {
    int t;
    cin >> t;
    while (t--) {
        cin >> n;
        for (int i = 1; i <= n; i++) {
            cin >> a[i][0] >> a[i][1] >> a[i][2];
        }
        memset(st, 0, sizeof st);
        ans = false;
        dfs(0, 0);
        if (ans)cout << "YES" << endl;
        else cout << "NO" << endl;
    }
 
 
    return 0;
}

c.接龙序列(线性dp)

思路：

凭感觉就是dp问题，但是需要换一下题意，题目求最少删除多少个数可以满足接龙序列，我们可以求最长的接龙序列的长度，这样再用n减去这个最大值就是最少删除的元素个数了。

类似于求最长上升子序列，先考虑二维状态转移方程

设dp[i][k]为以第i个元素为尾元素且最后一位数位为k的最长接龙序列的长度。

   for(int i=1;i<=n;i++){
        int k1=gethh(a[i]);//a[i]的第一位数
        int k2=a[i]%10;//a[i]的最后一位位数
        f[i][k2]=1;//初始化长度为1
        for(int j=1;j<i;j++){//从前遍历，更新f[i][k2].
            f[i][k2]=max(f[j][k1]+1,f[i][k2]);
            ans=max(ans,f[i][k2]);
        }
        // f[k2]=max(f[k1]+1,f[k2]);
        // ans=max(ans,f[k2]);
        
    }

假设一个元素的第一位数是k1，最后一位是k2，那么这个数的上一个数的最后一位数必须是k1，也就是f[j][k1],要取最长，所以 f[i][k2]=max(f[j][k1]+1,f[i][k2]).

优化

显然这种是超时的，能不能优化一层for循环呢？通过观察我们可以发现，对于第i个元素，我们其实没有必要再一直往前遍历，我们只需要找到上一个以k1结尾的数的值，并更新以k2结尾的数的值就行了。所以我们可以用f[i]表示以位数为i结尾的最长接龙序列的长度是多少就好了。

代码：

#include<iostream>
#include<math.h>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e5+10;
int f[10];
int a[N];
int s[10];
int get_n(int x){//计算x的位数
    int res=0;
    while(x){
        x/=10;
        res++;
    }
    return res;
}
int gethh(int x){//计算x的第一位数
    int k=get_n(x);
    int hh=x/pow(10,k-1);
    return hh;
}
int main(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    
     int ans=0;
    for(int i=1;i<=n;i++){
        int k1=gethh(a[i]);//a[i]的第一位数
        int k2=a[i]%10;//a[i]的最后一位位数
        f[k2]=max(f[k1]+1,f[k2]);
        ans=max(ans,f[k2]);
    }
    cout<<n-ans<<endl;
    return 0;
    
}

d.岛屿个数(bfs)

思路：

不同的岛屿比较好判断，但是需要考虑的就是怎么判断某个岛屿是不是子岛屿，也就是当前这个岛屿在不在某个环内。

我们可以优先遍历外面的海水，也就是地图最边框的海水地区。

考虑这样一个事实，如果最外层的海水存在，那么这些海水一定不在环内。且，最外层的海水bfs（只遍历相邻海水）一遍后一定能遍历完整个地图不在环内的海水。

于是乎，bfs一遍最外层的海水并标记后，对于海水而言，我们就能区分，在环内的海水和不在环内的海水。

这样一来，我们再把 在环内的海水全部变成陆地！这样一来，子岛屿和父岛屿就变成一个个整体了。

这个时候我们再计算地图岛屿的数量，就是答案了 

代码：

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
const int N = 60;
typedef pair<int, int> PII;
int m, n;
char g[N][N];
bool st[N][N];//标记哪些坐标被遍历过了
int dx[] = { 1,0,-1,0 }, dy[] = { 0,1,0,-1 };//遍历岛屿的位移偏移量
int dxx[] = { 0,-1,-1,-1,0,1,1,1 }, dyy[] = { -1,-1,0,1,1,1,0,-1 };//遍历海水的位移偏移量
int ans;
void bfs1(int x, int y) {//第一次遍历海水
    queue<PII> q;
    q.push({ x,y });
    while (!q.empty()) {
        int sz = q.size();
        for (int i = 0; i < sz; i++) {
            auto it = q.front();
            q.pop();
            int xx = it.first;
            int yy = it.second;
            // g[xx][yy]=1;
            if (st[xx][yy])continue;
            st[xx][yy] = true;
            for (int j = 0; j < 8; j++) {
                int a = dxx[j] + xx;
                int b = dyy[j] + yy;
                if (a >= 0 && a < m && b >= 0 && b < n && g[a][b] == '0' && !st[a][b]) {
                    q.push({ a,b });
                }
            }
        }
    }
}
void bfs2(int x, int y) {//遍历岛屿
    queue<PII> q;
    q.push({ x,y });
    while (!q.empty()) {
        int sz = q.size();
        for (int i = 0; i < sz; i++) {
            auto it = q.front();
            q.pop();
            int xx = it.first;
            int yy = it.second;
            // g[xx][yy]=1;
            if (st[xx][yy])continue;
            st[xx][yy] = true;
            for (int j = 0; j < 4; j++) {
                int a = dx[j] + xx;
                int b = dy[j] + yy;
                if (a >= 0 && a < m && b >= 0 && b < n && g[a][b] == '1' && !st[a][b]) {
                    q.push({ a,b });
                }
            }
        }
    }
    return;
}
 
int main() {
    int t;
    cin >> t;
    while (t--) {
        memset(st, false, sizeof st);
        cin >> m >> n;
        for (int i = 0; i < m; i++) {//存图
            for (int j = 0; j < n; j++) {
                cin >> g[i][j];
            }
        }
        //开始遍历一定不在环内的海水
        for (int j = 0; j < n; j++) {
            if (!st[0][j] && g[0][j] == '0') {
                bfs1(0, j);
            }
            if (!st[m - 1][j] && g[m - 1][j] == '0') {
                bfs1(m - 1, j);
            }
        }
 
        for (int i = 0; i < m; i++) {
            if (!st[i][0] && g[i][0] == '0') {
                bfs1(i, 0);
            }
            if (!st[i][n - 1] && g[i][n - 1] == '0') {
                bfs1(i, n - 1);
            }
        }
        //把在环内的海水设置为陆地
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (!st[i][j]) {
                    g[i][j] = '1';
                }
            }
        }
 
        ans = 0;
        //计算岛屿数量
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (!st[i][j] && g[i][j] == '1') {
                    ans++;
                    bfs2(i, j);
                }
            }
        }
        cout << ans << endl;
 
    }
 
    return 0;
}

e.字串简写（前缀和）

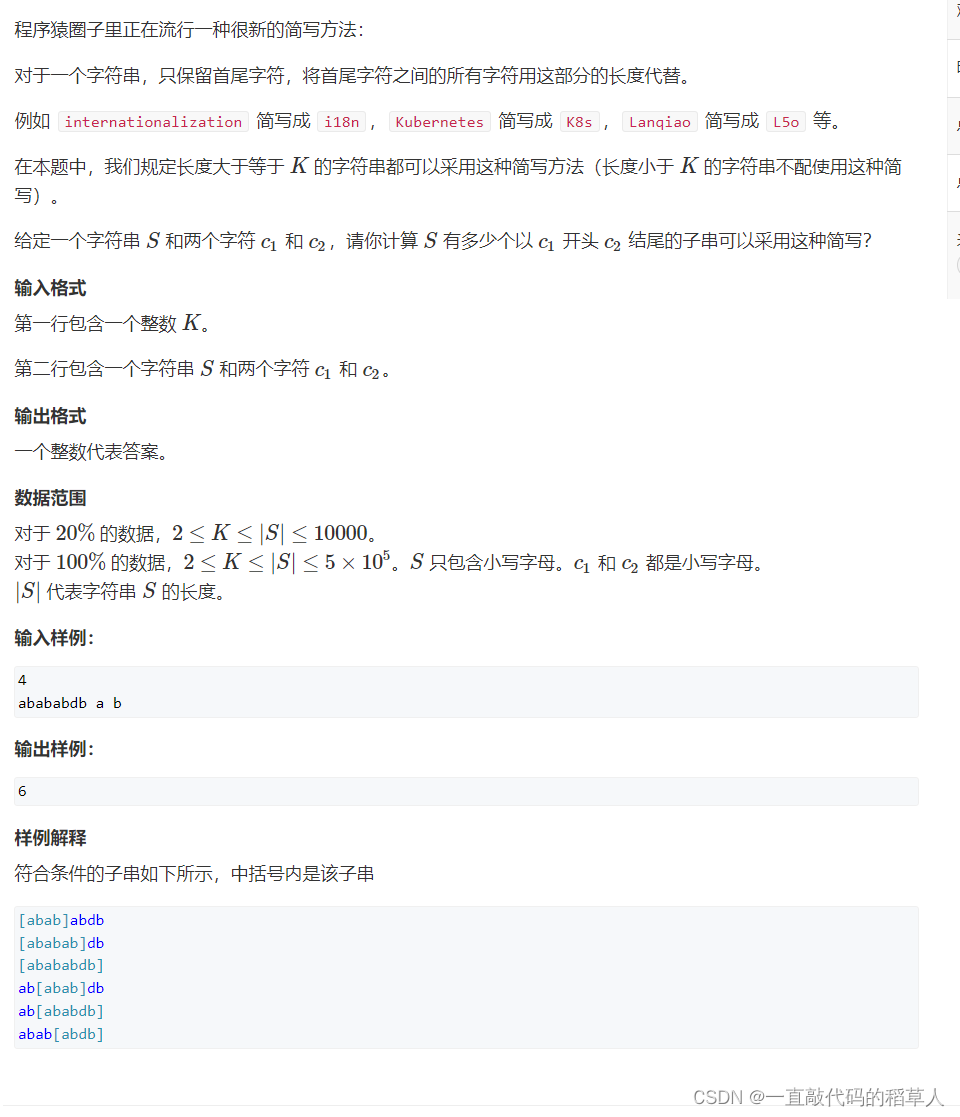
思路：

遍历整个字符串，用一个s数组维护c1的区间和，s[i]表示string S中0到i的c1的个数。再遍历一遍字符串S，如果遍历到了c2,前面有多少个c1就表示有多少个不同的子串能符合题目要求。也就是计算出以当前位置为末尾，长度大于k的的子串的c1的个数，就是s[i-k+1]。

代码：

 
#include<iostream>
#include<algorithm>
#include<vector>
#include<string>
using namespace std;
 
int main()
{
    int k;
    char a, b;
    string str;
    cin >> k >> str >> a >> b;
    int n = str.size();
    //int ans;
    vector<long long > s(n, 0);
    if (str[0] == a)s[0] = 1;
    for (int i = 1; i < n; i++) {
        if (str[i] == a)s[i] = 1;//如果是c1我们就把这个位置标记为1，方便前缀和计算
        s[i] += s[i - 1];
    }
    long long ans = 0;
    for (int i = 0; i < n; i++) {
        if (i >= k - 1 && str[i] == b) {
            ans += s[i - k + 1];
        }
    }
    cout << ans << endl;
    return 0;
}

f整数删除（优先队列，双链表）

思路：

这题需要思考如何每次都能找到最小的数？以及删除一个数后如何调整剩下元素的相对位置？

第一点我们可以用优先队列来解决，也就是最小堆。顺便将原始下标存进去。

第二点我们可以用双链表来存储下标的位置关系。用l[i],r[i]分别表示下标为i的元素的右边和左边的元素的下标，这样一来，一旦我们决定要删除某一个数，修改r[i]和l[i]就可以继续维护一个彼此相邻的数组了。

除此之外，由于每删除一个数，隔壁的数的值都要加上这个数，我们又不好直接取出隔壁的数（都放在优先队列里的），所以我们可再维护一个数组cnt[i]表示下标为i的元素还需要增加的值。

值得注意的是，我们需要判断当前取出的元素有可能不是最小值，因为有可能他还要加上cnt[i],所以取出来一个数后，要判断如果cnt[i]不为0的，表示之前删除过这个数的隔壁的数，所以要将取出来的数加上cnt[i]后再放回去，并将cnt[i]置为0。如果cnt[i]为0，意味着目前取出来的数一定是最小值，那么我们就把它删除，并修改其隔壁数的r[i]和l[i],以及cnt[i].

最后队列剩下的元素我们还需要根据按下标顺序输出

代码

#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
const int N=5e5+10;
typedef long long LL;
typedef pair<LL,int> PII;
LL cnt[N];
int l[N],r[N];
LL a[N];
int main(){
    int n,k;
    cin>>n>>k;
    priority_queue<PII,vector<PII>,greater<PII>>q;//最小堆
    r[0]=1;//边界0
    l[n+1]=n;//边界n+1
    for(int i=1;i<=n;i++){
        scanf("%lld",&a[i]);
        q.push({a[i],i});//元素的值在左边，最小堆默认按左边第一个值排序
        r[i]=i+1;//模拟双链表
        l[i]=i-1;
    }
    
    while(q.size()!=n-k){//要删除k个元素
        auto it=q.top();
        q.pop();
        LL v=it.first;
        int dix=it.second;
        if(cnt[dix]){
            v+=cnt[dix];
            q.push({v,dix});
            cnt[dix]=0;
        }else{
            cnt[l[dix]]+=v;//修改隔壁的增量
            cnt[r[dix]]+=v;
            l[r[dix]]=l[dix];//双链表的删除操作
            r[l[dix]]=r[dix];
            
        }
    }
 
    while(!q.empty()){//剩下元素按下标存入数组a中
        auto it=q.top();
        q.pop();
        a[it.second]=it.first;
    }
    
    int ne=0;
    while(r[ne]!=n+1){//遍历双链表
        printf("%lld ",a[r[ne]]+cnt[r[ne]]);
        ne=r[ne];
    }
    
    return 0;
}

g.景区导游(LCA)

思路：

如何计算树中任意两个点u,v的距离？首先用一个dis数组存每个节点到根节点的距离，再找到这两个节点的最近公共祖先节点k，它们之间的距离就等于 dis[u]+dis[v]-2*dis[k]

求最近公共祖先用LCA算法

答案求跳过Ai节点的路径总长度，我们可以先把总路径长度ans求出来，例如样例的路线 2-->6--> 5--> 1 .

假如跳过节点5,路径长度就变成了2-->6的长度+ 6-->1的长度

设path(v,u)表示两个节点在树上的距离

也就是说假如我们要跳过a[i]，那么剩下路线总长度为

ans-getpath(a[i], a[i - 1])-getpath(a[i + 1], a[i])+ getpath(a[i + 1], a[i - 1])

代码：

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int f[N][21];
int deth[N];
LL dis[N];
int a[N];
vector<int>e[N], w[N];
 
void dfs(int u, int fa) {
    deth[u] = deth[fa] + 1;
    f[u][0] = fa;
 
    for (int i = 1; i <= 20; i++) {
        f[u][i] = f[f[u][i - 1]][i - 1];
    }
    int sz = e[u].size();
    for (int i = 0; i < sz; i++) {
        int v = e[u][i], s = w[u][i];
        if (v == fa)continue;
        dis[v] = dis[u] + s;
        //cout<<u<<"-->"<<v<<" ll "<<s<<" kk "<<dis[u]<<endl;
        dfs(v, u);
    }
}
 
int LCA(int u, int v) {
    if (deth[u] < deth[v])swap(u, v);
    for (int i = 20; i >= 0; i--) {
        if (deth[f[u][i]] >= deth[v]) {
            u = f[u][i];
        }
    }
    if (u == v)return u;
    for (int i = 20; i >= 0; i--) {
        if (f[u][i] != f[v][i]) {
            u = f[u][i];
            v = f[v][i];
        }
    }
    return f[u][0];
}
 
LL getpath(int u, int v) {
    if (!u || !v)return 0;
    return dis[u] + dis[v] - 2 * dis[LCA(u, v)];
}
 
int main() {
    int n, k;
    cin >> n >> k;
    for (int i = 0; i < n - 1; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        e[a].push_back(b);
        w[a].push_back(c);
        e[b].push_back(a);
        w[b].push_back(c);
 
    }
 
    dfs(1, 0);
    LL ans = 0;
    cin >> a[0];
    for (int i = 1; i < k; i++) {
        cin >> a[i];
        ans += getpath(a[i], a[i - 1]);
    }
    for (int i = 0; i < k; i++) {
        LL d1 = 0;
        if (i != 0)d1 += getpath(a[i], a[i - 1]);
        if (i != k - 1)d1 += getpath(a[i + 1], a[i]);
        LL d2 = 0;
        if (i != 0 && i != k - 1) {
            d2 += getpath(a[i + 1], a[i - 1]);
        }
        cout << ans - d1 + d2 << " ";
    }
 
    return 0;
}