Java排序算法（五）归并排序_归并排序的虚段

Java排序算法（一）冒泡排序
Java排序算法（二）选择排序
Java排序算法（三）插入排序
Java排序算法（四）希尔排序

归并排序

算法思想

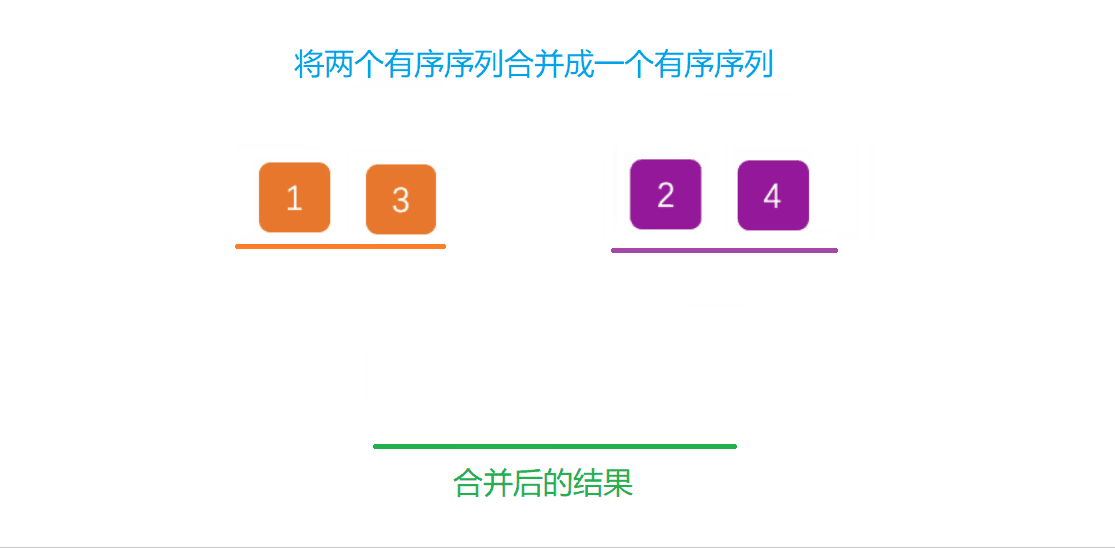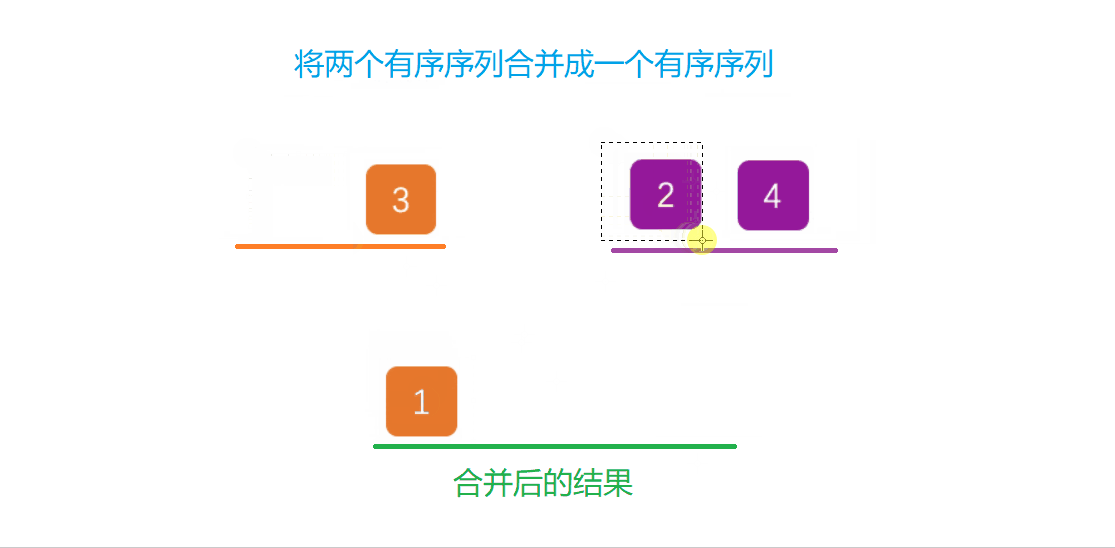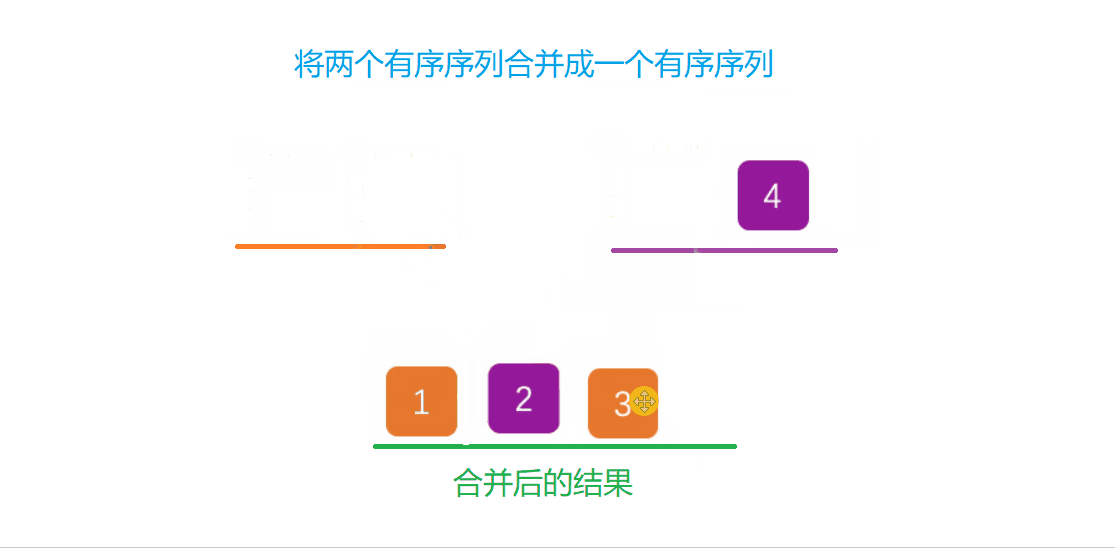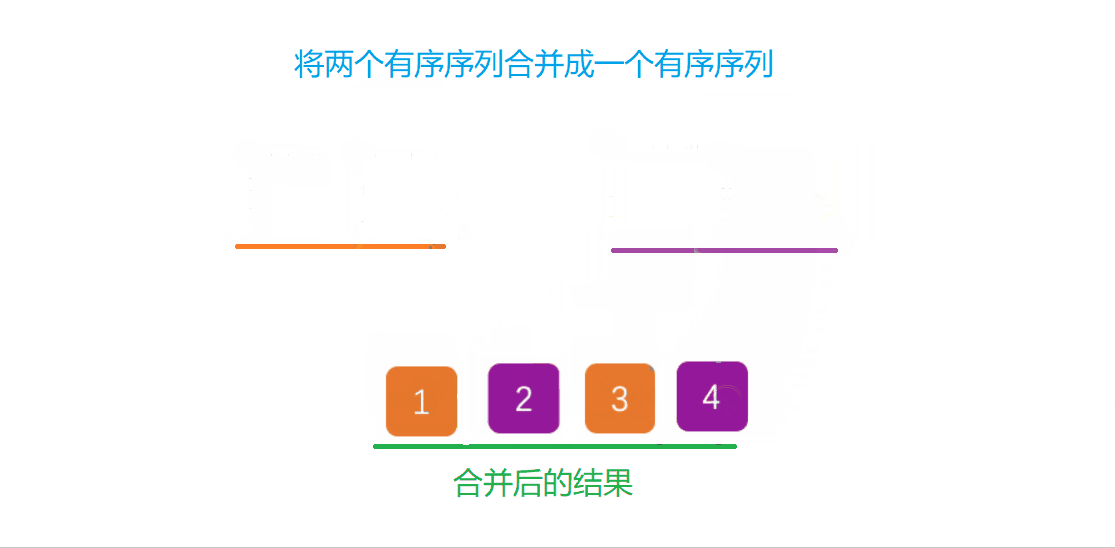
归并排序建立在归并的有效操作上进行排序，主要采用分治法将已有序的子序列合并，得到完全有序的序列。即先让每一小段有序，再让小段之间变得有序。若将两个有序合成一个有序段，这又称为二路归并。
补充：分治法，字面意思是“分而治之”，就是把一个复杂的问题分成两个或多个相同或相似的子问题，再把子问题分成更小的子问题直到最后子问题可以简单地直接求解，原问题的解即子问题的解的合并。
将两个有序序列合并成一个有序序列演示：

算法描述

①开始以间隔为1的进行归并，也就是说，第一个元素跟第二个进行归并。第三个与第四个进行归并；
②然后，再以间隔为2的进行归并，1-4进行归并，5-8进行归并；
③再以2 * 2的间隔进行归并，同理直到2 * k超过序列的长度为止。
④当不够两组进行归并时，如果超过k个元素元素，仍然进行归并；如果剩余元素不超过k个元素，那么直接复制给中间元素。

动画演示

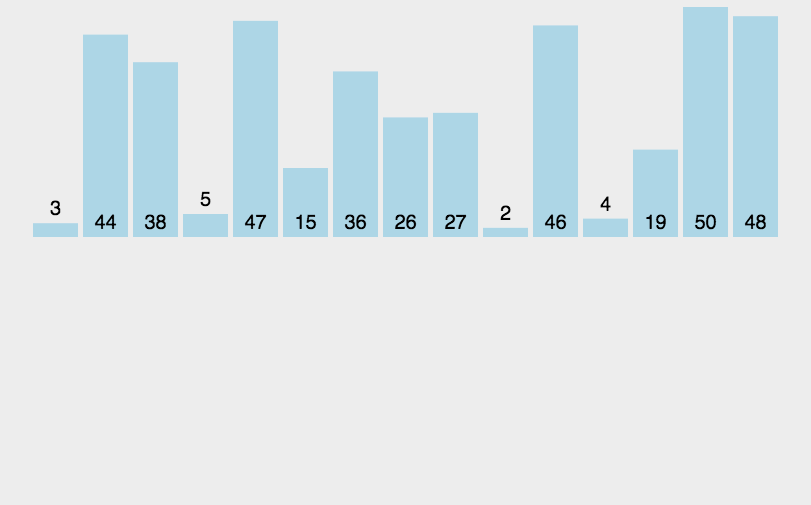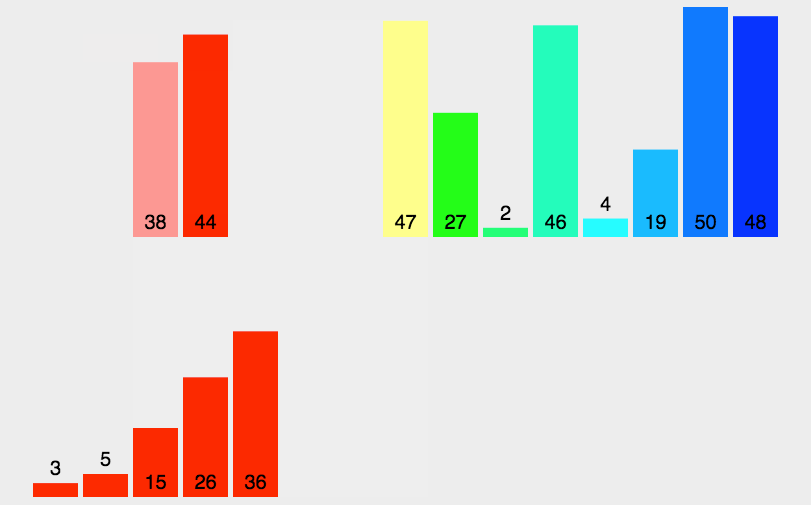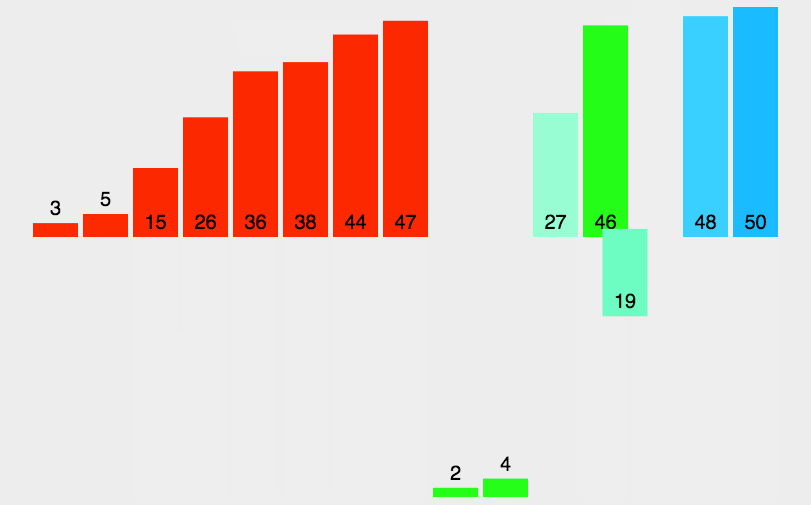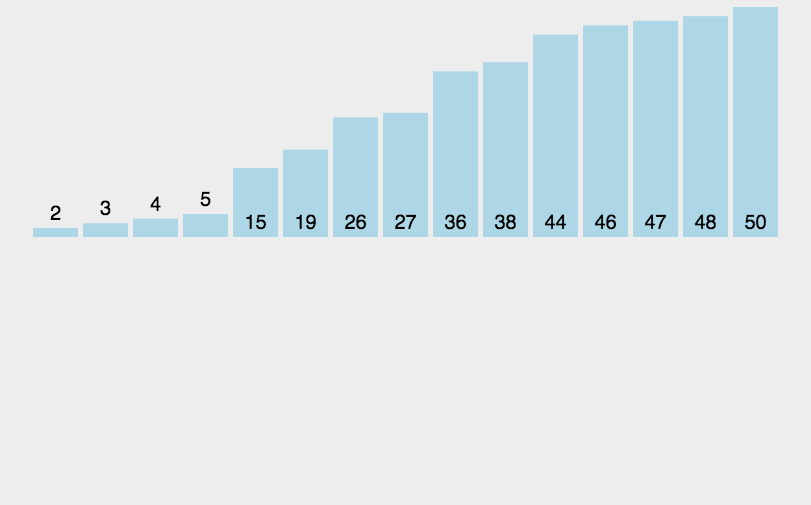
算法详解

将序列 26 53 67 48 57 13 49 32 60 50 进行归并排序。

在进行归并排序过程中我们需要考虑三种特殊情况：
第一种： 最后一个小组没有与之对应的小组存在，则不需要排序。

第二种： 最后一个小组没有与之对应的小组存在，且最后一个小组中的元素个数不够gap个，则不需要排序。

第三种： 最后一个小组有与之对应的小组存在，但是与之对应的小组中的元素个数不够gap个，则需要控制与之对应小组的边界。

代码演示

import java.util.Arrays;

public class SortTest05 {
    private static void marge(int[] arr,int gap,int[] brr){
        int left1 = 0;//第一个序列左边界
        int right1 = left1 + gap - 1; //第一个序列右边界
        int left2 = right1 + 1;//第二个序列左边界
        //第二个序列的右边界 考虑两种情况 1）其序列左边界 + gap - 1如果超过序列长度，则右边界直接等于数组的最大下标
        //                          2)其序列左边界 + gap - 1如果没有超过序列长度，则右边界等于 left2 + gap - 1
        int right2 = left2 + gap - 1 > arr.length - 1  ? arr.length - 1 : left2 + gap - 1;

        //开辟一个与数组arr相同长度的brr数组，用来在归并排序过程中存放已经完成排序的序列

        int j = 0;//控制新数组下标
        while (left2 < arr.length) {
            //合并两个有序序列
            while (left1 <= right1 && left2 <= right2) {
                if (arr[left1] < arr[left2]) {
                    brr[j++] = arr[left1++];
                }else {
                    brr[j++] = arr[left2++];
                }
            }

         //当其中一个序列中元素全部排序完，另一个序列剩余元素直接归入brr数组中
            if (left1 > right1) {
                while(left2 <= right2) {
                    brr[j++] = arr[left2++];
                }
            }
            if (left2 > right2) {
                while (left1 <= right1) {
                    brr[j++] = arr[left1++];
                }
            }

          //更新两个待排序序列的左下标和右下标
            left1 = right2 + 1;
            right1 = left1 + gap - 1;
            left2 = right1 + 1;
            right2 = left2 + gap - 1 > arr.length - 1 ? arr.length - 1 : left2 + gap - 1;
        }

        //只剩一个归并字段
        while(left1 <= arr.length - 1) {
            brr[j++] = arr[left1++];
        }

        System.arraycopy(brr,0,arr,0,arr.length);
    }

    public static void margeSort(int[] arr) {
        //安全检测
        if (arr == null || arr.length == 1) {
            return;
        }

        int[] brr = new int[arr.length];
        for (int i = 1; i < arr.length ; i*=2) {
            marge(arr,i,brr);
        }
    }

    public static void main(String[] args) {
        int[] arr = {26,53,67,48,57,13,49,32,60,50};
        System.out.println("排序前:" + Arrays.toString(arr));
        margeSort(arr);
        System.out.println("排序后:" + Arrays.toString(arr));
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

运行结果：

归并排序算法分析