- 1vue 使用自定义标签URL Protocol 调用本地exe 并传参
- 2华为OD技术面试手撕代码真题复盘_华为od前端技术面手撕
- 3qt 打印日志
- 4分子动力学模拟的理论与实战-阅读笔记_mmff94力场迭代 代码
- 5如何在Centos7下安装Nginx_centos nginx
- 6windows Server 2003 MSCS双机热备份
- 7什么是Spring?它有哪些好处?_csdn中spring是什么
- 8azure未连接_处理影响Azure成本的未使用和不必要的资源
- 9Java常见注解_untracked files prevent merge
- 10python爬虫②-----urllib高级用法_req=urllib.request.request(start_url)
蓝桥备赛——矩阵读入
赞
踩
题目描述


如上图所示,是一道有关二维前缀和的问题,因为涉及到二维,肯定就是以矩阵的形式进行读入的。
为此,针对矩阵的读入形式进行总结,可以大致总结出两种类型如下:
二维列表推导式
- n, m, k = map(int, input().split())
- mat = []
- for i in range(n):
- mat.append(list(map(int, input().split())))
- pre = [[0 for _ in range(m)] for _ in range(n + 1)]
- for i in range(1, n + 1):
- for j in range(m):
- pre[i][j] = pre[i - 1][j] + mat[i - 1][j]
可以看到上面代码的
pre = [[0 for _ in range(m)] for _ in range(n + 1)]
表示的是对于第一个[ ]中的元素是生成一个行向量,对于外面的第二个[ ]表示的是生成多少行的列表。
经过上面的代码,可以获得一个列表为
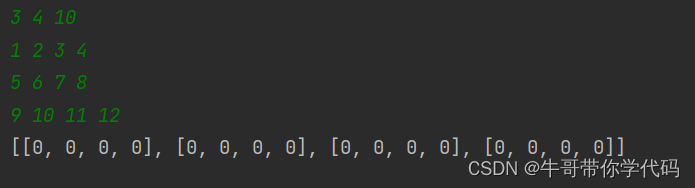
即获得了一个所有元素都为0的列表。后面再不停地读入元素进行原内容覆盖。
自创的方法
- n,m,k=map(int,input().split())
- mas=[]
- for i in range(n):
- matrix = []
- matrix.extend(map(int,input().split()))
- mas.append(matrix)
- print(mas)
同样是先读入数据,不过需要额外创建一个列表作为中转,将数据读入后,再将其作为整体append到一个新的列表,即可达到上面二维列表推导式的效果。
与上面方法不同的地方是,不需要再重新将元素全部覆盖,所录入列表的即为最终数据。
AC Code
- n, m, k = map(int, input().split())
- mat = []
- for i in range(n):
- mat.append(list(map(int, input().split())))
- pre = [[0 for _ in range(m)] for _ in range(n + 1)]
- for i in range(1, n + 1):
- for j in range(m):
- pre[i][j] = pre[i - 1][j] + mat[i - 1][j]
- ans = 0
- for i in range(n):
- for j in range(i, n):
- l, r, sum = 0, 0, 0
- while r < m:
- sum += pre[j + 1][r] - pre[i][r]
- while sum > k:
- sum -= pre[j + 1][l] - pre[i][l]
- l += 1
- ans += r - l + 1
- r += 1
- print(ans)
现在来解释一下上面的代码
- n, m, k = map(int, input().split())
- mat = []
- for i in range(n):
- mat.append(list(map(int, input().split())))
- pre = [[0 for _ in range(m)] for _ in range(n + 1)]
- for i in range(1, n + 1):
- for j in range(m):
- pre[i][j] = pre[i - 1][j] + mat[i - 1][j]
这块代码的作用就是读入相关数据
- ans = 0
- for i in range(n):
- for j in range(i, n):
- l, r, sum = 0, 0, 0
- while r < m:
- sum += pre[j + 1][r] - pre[i][r]
- while sum > k:
- sum -= pre[j + 1][l] - pre[i][l]
- l += 1
- ans += r - l + 1
- r += 1
- print(ans)
上面代码的作用就是对应:
for i in range(1, n + 1): for j in range(m): pre[i][j] = pre[i - 1][j] + mat[i - 1][j]:计算前缀和矩阵pre。对于pre[i][j],表示原始矩阵中第i-1行(因为前缀和矩阵行数比原始矩阵多了1)以及前j列的元素之和。
ans = 0:初始化变量ans,用于记录满足条件的子矩阵数量。
for i in range(n): for j in range(i, n)::遍历所有可能的子矩阵的上边界i和下边界j。
l, r, sum = 0, 0, 0:初始化左边界l、右边界r以及子矩阵元素之和sum。
while r < m: sum += pre[j + 1][r] - pre[i][r]:在子矩阵的右边界r小于列数m时,计算子矩阵在当前列的元素之和。
while sum > k: sum -= pre[j + 1][l] - pre[i][l] l += 1:如果子矩阵的元素之和超过了限定值k,则移动左边界l,直到子矩阵的元素之和不再超过k。
ans += r - l + 1:更新满足条件的子矩阵数量。
r += 1:向右移动子矩阵的右边界r。
print(ans):输出满足条件的子矩阵数量。该算法的时间复杂度为O(n^3 * m),因为有三层嵌套循环分别遍历行、列和子矩阵。


