二分查找(1)-左边界_二分查找左边界

二分查找原理

首先二分查找主要用于有序的数组当中。
其次二分查找利用有序性质排除不符合数组的一半然后不断逼近正确数组

算法思路

算法思路：假设目标值在闭区间[l, r]中， 每次将区间长度缩小一半，当l = r时，我们就找到了目标值。

算法模板

int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (A[mid]>=target) r = mid;
        else l = mid + 1;
    }
    return l;
}
1
2
3
4
5
6
7
8
9
10

图解

在1 3 4 5 6 8查找目标5的位置

首先令：

数组为A
左边界L=0
右边界r=n
mid=(r+l)/2

第一次判断如果mid的值大于等于目标值则R=mid,否则L=mid+1;

为什么判断值是大于等于而不是大于

因为目标值可能是多个，我们目的是判断边界不是查找值，A[mid]和目标值相等时mid不一定指向左边界

为什么等于放在大于(R=mid)判断中而不是小于(L=mid)当中

因为我们找的是左边界，如果等于放在小于时。如下图的边界就在【mid, R】直接查找（错误）因此只能R=mid

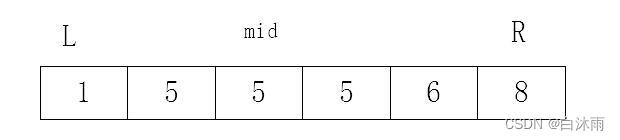
当 目标值不存在是L指向的是第一个比目标值大的数

二分查找参考awcing
二分查找左边界例题

//AC代码
class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        if(nums[nums.size()-1]<target)return nums.size();
        int l=0,r=nums.size()-1;
        while(l<r){
            int mid=l+r>>1;
            if(nums[mid]>=target)r=mid;
            else l=mid+1;
        }
        return l;                                                          
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14