二叉树的三种遍历方法及实现代码_二叉树的三种遍历代码

.前言
二叉树：指只有两个子节点，共三个节点的树：根节点、左子节点、右子节点。

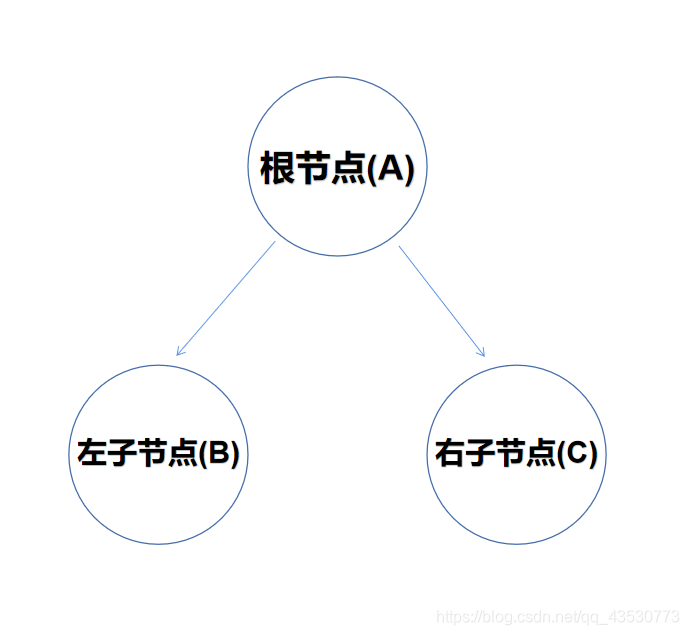
根据三个节点的遍历的顺序分为前序、中序和后序遍历三种。

注：前面的方位词修饰的根节点（我觉得知道这个就能记住了）

前序：
根节点->左子节点->右子节点：A->B->C

中序：
左子节点->根节点->右子节点：B->A->C

后序：
左子节点->右子节点->根节点：B->C->A

当遇到的子节点并非是叶节点时，就嵌套上述步骤读取。

三种遍历中较重要的是中序遍历，因为很多排序（如堆排序）都要利用到。

用例示范：

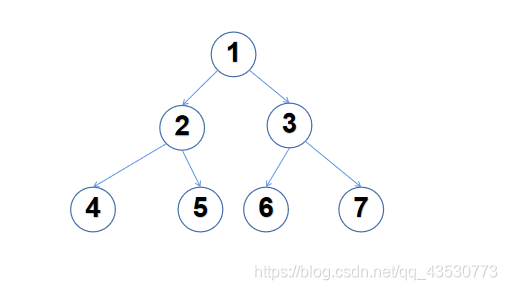
前序：

#include <iostream>
#include <vector>
#include <stack>

using namespace std;

//树节点
struct Node
{
	int data;
	Node* left, * right;
	Node(int x):data(x),left(0),right(0){}
};

int main()
{
	//第一层
	Node* n1 = new Node(1);
	//第二层
	Node* n2 = new Node(2);
	Node* n3 = new Node(3);
	//第三层
	Node* n4 = new Node(4);
	Node* n5 = new Node(5);
	Node* n6 = new Node(6);
	Node* n7 = new Node(7);

	//造树
	n1->left = n2;
	n1->right = n3;

	n2->left = n4;
	n2->right = n5;
	n3->left = n6;
	n3->right = n7;

	//通过栈实现深度遍历
	stack<Node*> nodeStack;

	//先将根节点压入栈
	nodeStack.push(n1);

	//当栈不为空时，则不断弹出
	while (!nodeStack.empty())
	{
		//获取栈顶元素，并输出其值
		Node* node = nodeStack.top();
		cout << node->data << " ";
		//弹出栈顶元素
		nodeStack.pop();

		//按照先压右子节点后压左子节点的顺序，判断左右子树是否为空，若不为空，则压入栈
		if (node->right)
		{
			nodeStack.push(node->right);
		}
		if (node->left)
		{
			nodeStack.push(node->left);
		}

	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

中序遍历：

#include <iostream>
#include <vector>
#include <stack>

using namespace std;

//树节点
struct Node
{
	int data;
	Node* left, * right;
	Node(int x):data(x),left(0),right(0){}
};

int main()
{
	//第一层
	Node* n1 = new Node(1);
	//第二层
	Node* n2 = new Node(2);
	Node* n3 = new Node(3);
	//第三层
	Node* n4 = new Node(4);
	Node* n5 = new Node(5);
	Node* n6 = new Node(6);
	Node* n7 = new Node(7);

	//造树
	n1->left = n2;
	n1->right = n3;

	n2->left = n4;
	n2->right = n5;
	n3->left = n6;
	n3->right = n7;

	//通过栈实现深度遍历
	stack<Node*> nodeStack;

	//确定根节点
	Node* node = n1;

	//当栈不为空或当前指针不为空时，则不断弹出
	while (!nodeStack.empty()||node)
	{
		//获取子树的最左子叶节点
		//当当前指针并非是个空指针时，则不断压入自身，并把自己的左子节点更新为当前节点
		//而当当前指针为空指针时，有两种情况：
		//1、表明指针所在的子树已经达到叶子节点了，可以开始中序遍历了
		//2、当前是一个 已被遍历的 左子叶节点的 右子节点，此时右子节点自然为空
		while (node)
		{
			nodeStack.push(node);
			node = node->left;
		}
		//此时若栈不为空，则表明此刻指针为子树未遍历的最左子叶节点
		if(!nodeStack.empty())
		{
			//获取栈顶元素，并输出，然后弹出
			node = nodeStack.top();
			cout << node->data << " ";
			nodeStack.pop();
			//将指针更新为当前节点的右子节点，
			//若当前节点为子叶节点，那更新后指针必为空，因此会被跳过从而读取根节点
			//若更新后非空，则会重新搜索子树的最左子叶节点
			node = node->right;
		}

	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

后序遍历：
后序遍历的顺序是左子节点->右子节点->根节点，在形式上其实很像是先序遍历的逆转，所以这里直接用翻转函数便可。

#include <iostream>
#include <vector>
#include <stack>

using namespace std;

//树节点
struct Node
{
	int data;
	Node* left, * right;
	Node(int x):data(x),left(0),right(0){}
};

int main()
{
	//第一层
	Node* n1 = new Node(1);
	//第二层
	Node* n2 = new Node(2);
	Node* n3 = new Node(3);
	//第三层
	Node* n4 = new Node(4);
	Node* n5 = new Node(5);
	Node* n6 = new Node(6);
	Node* n7 = new Node(7);

	//造树
	n1->left = n2;
	n1->right = n3;

	n2->left = n4;
	n2->right = n5;
	n3->left = n6;
	n3->right = n7;

	//存取数据的数组，方便翻转
	vector<int> arr;

	//通过栈实现深度遍历
	stack<Node*> nodeStack;
	nodeStack.push(n1);

	//当栈不为空时不断弹出
	while (!nodeStack.empty())
	{
		//获取栈顶元素并弹出，且压入数组
		Node* node = nodeStack.top();
		nodeStack.pop();
		arr.push_back(node->data);

		//虽然在结构上跟先序遍历的结构的翻转类似，但要注意左右子树的读取顺序
		if(node->left)
		{
			nodeStack.push(node->left);
		}
		if (node->right)
		{
			nodeStack.push(node->right);
		}
	}
	//翻转数组即可
	reverse(arr.begin(), arr.end());
	for(vector<int>::iterator iter=arr.begin();iter!=arr.end();iter++)
	{
		cout << *iter << " ";
	}
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70