数据结构--树状数组

什么是树状数组？

树状数组或二叉索引树，顾名思义是一个有着树形结构的数组，主要用于高效地处理区间上的查询与搜索问题。需要提及的是树状数组能够解决的问题，使用线段树都能够解决，而线段树能够解决的问题，使用树状数组有可能不能解决，但树状数组优点在于的实现更加简单。

---

预备函数--Lowbit

Lowbit函数的功能为返回参数转为二进制后,最后一个1的位置所代表的十进制数值，例如：

22的二进制=（10110），从右向左最后一个1与其后面的0所组成的二进制数为（10），因此Lowbit(22)=2；

Lowbit函数的代码实现如下：

 
int lowbit(int t)
{
    return t&(-t);
}

树状数组结构分析

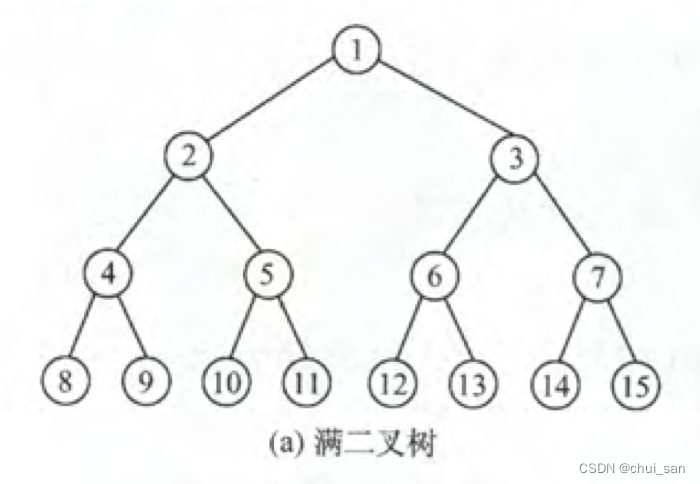
在一棵满二叉树中，如果我们人为的让其中的节点(A[i])表示子树的叶子节点的权值之和，我们则可以得出如下结论：

A[4]=A[8]+A[9]

A[5]=A[10]+A[11]

A[2]=A[4]+A[5]=A[8]+A[9]+A[10]+A[11]

A[6]=A[12]+A[13]

A[7]=A[14]+A[15]

A[3]=A[6]+A[7]=A[12]+A[13]+A[14]+A[15]

A[1]=A[2]+A[3]=A[4]+A[5]+A[6]+A[7]=A[8]+A[9]+A[10]+A[11]+A[12]+A[13]+A[14]+A[15]

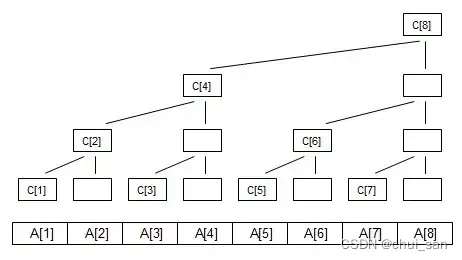
而树状数组可以看作是由一棵满二叉树经过变形得来，从上面的例子中我们不难发现在满二叉树中进行如上运算时每层的第偶数个节点均可以通过其父节点的数值减去其兄弟节点的数值来得到，所以我们可以通过这个性质删去其中的一些节点来简化这棵树。我们将满二叉树每一层上从左到右的第偶数个节点删去，再将未被删去的剩余的节点（每列的顶端节点）依次存入数组，这样我们就得到了一个树状数组。

这时假如我们想要求解原数组前四项之和即c[4]的值，我们就可以通过c[4]=c[2]+c[3]+A[4]=c[1]+c[3]+A[2]+A[4]=A[1]+A[2]+A[3]+A[4]来求解。

需要特别注意的是，结合Lowbit函数，我们可以发现在树状数组中一条非常重要的结论：节点x的父节点为x+Lowbit(x)。例如，c[2]的父节点为c[2+Lowbit(2)]=c[4]。

单点修改与区间查询

了解树状数组的结构和性质之后，我们来看树状数组的第一种常见操作：单点修改与区间查询

单点查询的核心并不只是更新原数组A中的某一个值而是继续向上更新树c中的值。

例如：当在A[1]加上值num时，即修改A[1]时，需要向上更新c[1],c[2],c[4],c[8]，将这4个节点每个节点的值加上num即可。由于c[1],c[2],c[4],c[8]中都包含有A[1]，所以在修改A[1]时实际上就是修改每一个包含A[1]的节点。根据树状数组的性质，我们只需要不断进行+Lowbit操作即可不断向上访问节点。

单点修改的代码实现如下：

void update(int i,int num)
{
    while(i<=n){
        C[i]+=num;
        i+=lowbit(i);
    }
}

 区间修改操作即求和，例如：原数组前7项和sum[7]可通过树状数组的性质进行快速求解，即sum[7]=c[4]+c[6]+c[7]。与单点修改一样，我们可以通过-Lowbit快速找到c[7]找到c[6]与c[4]的值。

int ask(x){
	int sum = 0;
	for(int i=x;i;i-=lowbit(i)){
		sum+=t[i];
	}
	return sum;
}

区间修改与单点查询

对于区间修改与单点查询操作，我们主要需要应用差分数组的性质。

对于区间修改操作，我们只需要对对应区间上的差分数组进行修改即可。例如，我们想要对区间为[L，R]上的数据进行+k操作，我们只需要修改对应的差分数组，即进行add(L，k)，add(R+1，-k)操作。

对于区间修改操作，代码如下：

int update(int pos,int k)
{
	for(int i=pos;i<=n;i+=lowbit(i))
	c[i]+=k;
	return 0;
}
update(L,k);
update(R+1,-k);

对于单点查询操作，同样应用差分数组的性质，求出差分数组对应的前缀和即可

对于单点查询操作，代码如下：

int ask(int pos)
{
	int ans=0;
	for(int i=pos;i;i-=lowbit(i)) ans+=c[i];
	return ans;
} 

例题及题解

洛谷CF44C

#include <iostream>
#define ll long long
#define lowbit(x) (x) & (-x)
 
using namespace std;
 
const int N = 110;
 
ll t[N];
 
ll n, m;
 
void add(ll x, ll k)
{
    for (ll i = x; i <= n; i += lowbit(i))
    {
        t[i] += k;
    }
}
 
ll ask(ll x)
{
    ll sum = 0;
    for (ll i = x; i; i -= lowbit(i))
    {
        sum += t[i];
    }
    return sum;
}
 
int main(void)
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
 
    cin >> n >> m;
 
    while (m--)
    {
        ll a, b;
        cin >> a >> b;
 
        add(a, 1);
        add(b + 1, -1);
    }
    for (ll i = 1; i <= n; i++)
    {
        if (ask(i) != 1)
        {
            if (ask(i) < 1)
            {
                cout << i << " " << 0 << endl;
            }
            else
                cout << i << " " << ask(i) << flush;
            return 0;
        }
    }
    puts("OK");
    return 0;
}

洛谷P1908

#include <iostream>
#include <algorithm>
#define ll long long
#define lowbit(x) (x) & (-x)
 
using namespace std;
 
const int N = 5e5 + 10;
 
ll n, m;
 
ll t[N], ranks[N];
 
struct point
{
    ll val, num;
} a[N];
 
void add(ll x, ll k)
{
    for (ll i = x; i <= n; i += lowbit(i))
    {
        t[i] += k;
    }
}
 
ll ask(ll x)
{
    ll sum = 0;
    for (ll i = x; i; i -= lowbit(i))
    {
        sum += t[i];
    }
    return sum;
}
 
bool cmp(point &a, point &b)
{
    if (a.val == b.val)
    {
        return a.num < b.num;
    }
    return a.val < b.val;
}
 
int main(void)
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
 
    cin >> n;
 
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i].val;
        a[i].num = i;
    }
 
    sort(a + 1, a + n + 1, cmp);
 
    for (int i = 1; i <= n; i++)
    {
        ranks[a[i].num] = i;
    }
 
    ll ans = 0;
 
    for (int i = 1; i <= n; i++)
    {
        add(ranks[i], 1);
        ans += i - ask(ranks[i]);
    }
 
    cout << ans << endl;
 
    return 0;
}