python算法：堆排序（Heap Sort）原理及算法实现，TopK问题_python小根堆排序

.堆排序（Heap Sort）

堆排序（英语：Heapsort）是指利用堆（heap）这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子节点的键值或索引总是小于（或者大于）它的父节点。

堆可看作是一个「完全二叉树」的结构：

根据父子节点之间的关系，堆又可大致分为两类（如下图所示）：

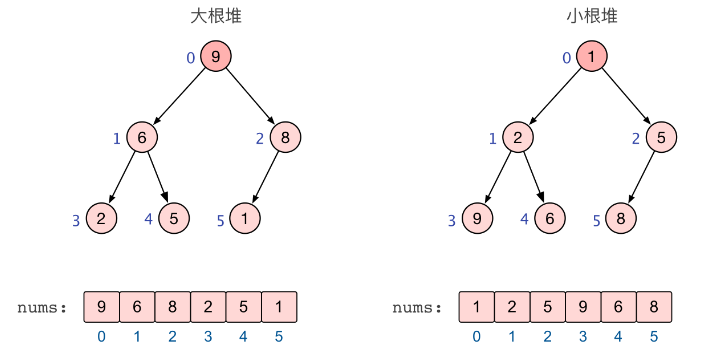
大根堆／大顶堆：每个节点的值均大于等于其左右孩子节点的值；

小根堆／小顶堆：每个节点的值均小于等于其左右孩子节点的值。

​

堆与排序：

案例：

假设有一个待排序的数组 nums=[5,2,1,9,6,8] 为例，讲解下如何构造大根堆，并实现其「升序排列」。

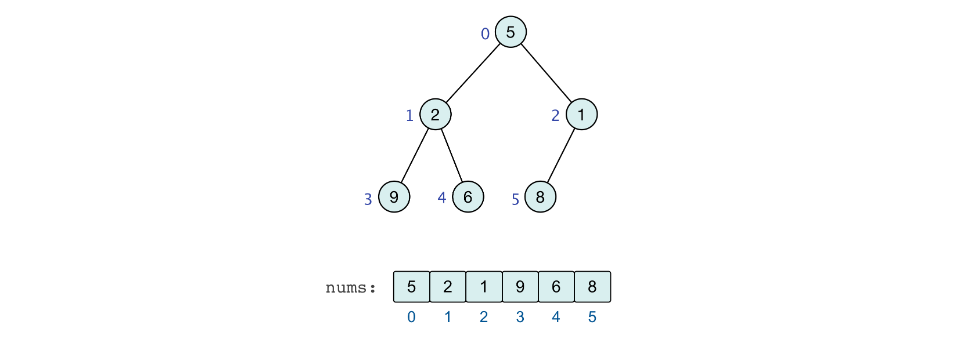
I. 构造大根堆

如何将一个完全二叉树构造成一个大顶堆？

一个很好的实现方式是从最后一个「非叶子节点」为根节点的子树出发，从右往左、从下往上进行调整操作。

对于以某个非叶子节点的子树而言，其基本的调整操作包括:

1、如果该节点大于等于其左右两个子节点，则无需再对该节点进行调整，因为它的子树已经是堆有序的；

2、如果该节点小于其左右两个子节点中的较大者，则将该节点与子节点中的较大者进行交换，并从刚刚较大者的位置出发继续进行调整操作，直至堆有序。

对于 nums=[9,6,8,2,5,1]，其堆排序基本步骤如下：

1、

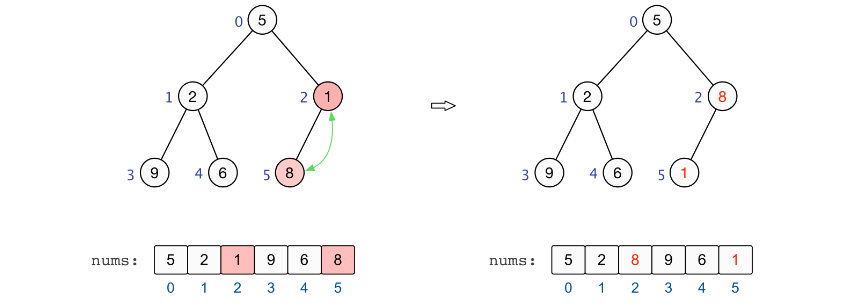
2、

3、

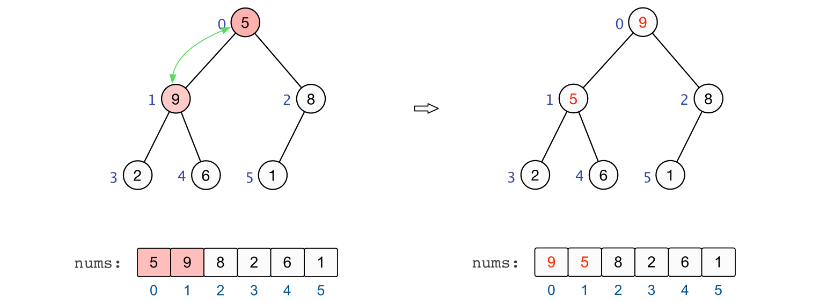
4、

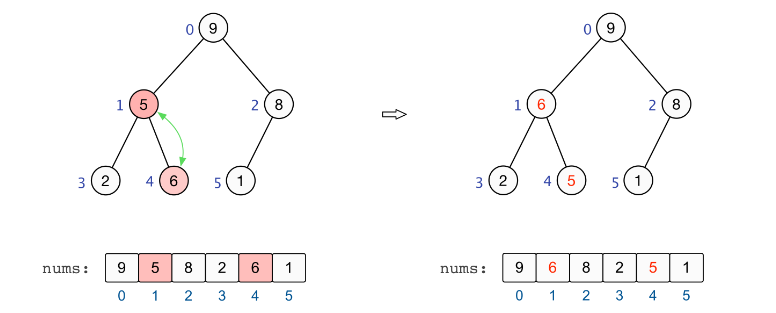
至此，全部的调整完毕，我们也就建立起了一个大根堆 ：

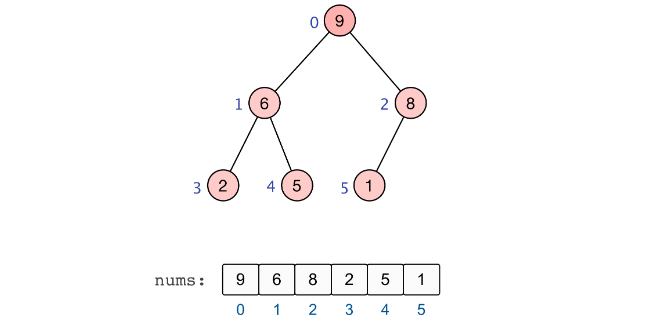
建立起一个大根堆后，便可以对数组中的元素进行排序了。总结来看，将堆顶元素与末尾元素进行交换，此时末尾即为最大值。除去末尾元素后，将其他 n−1 个元素重新构造成一个大根堆，继续将堆顶元素与末尾元素进行交换，如此便可得到原数组 n 个元素中的次大值。如此反复进行交换、重建、交换、重建，便可得到一个「升序排列」的数组。

最大元素：此时堆顶元素为最大值，将其交换到末尾，如下所示：

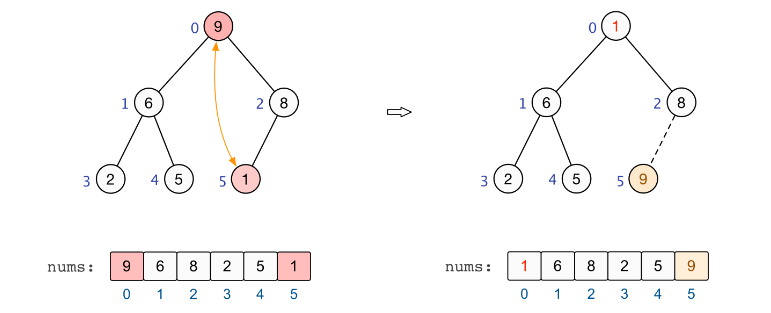
交换完成后，除去末尾最大元素，此时需要对堆进行重建，使得剩余元素继续满足大根堆的要求。如下所示：

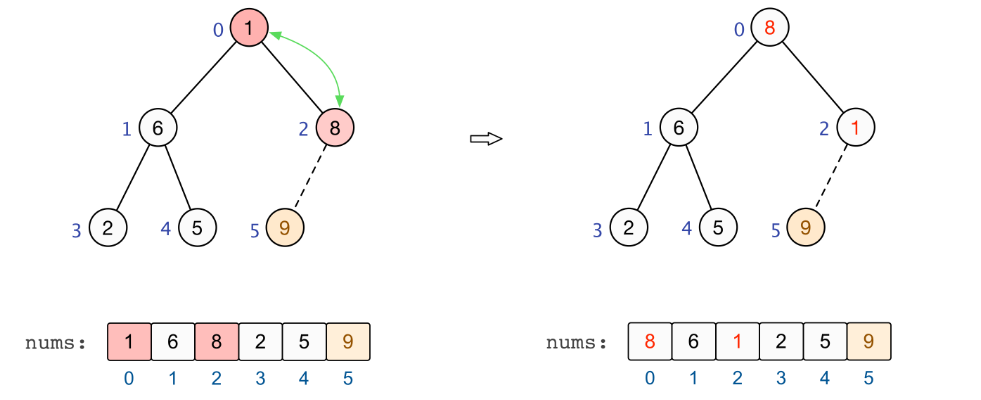
次大元素：此时堆顶元素为待排序元素中的最大值（即原数组中的次大值），将堆顶元素交换到末尾，如下所示：

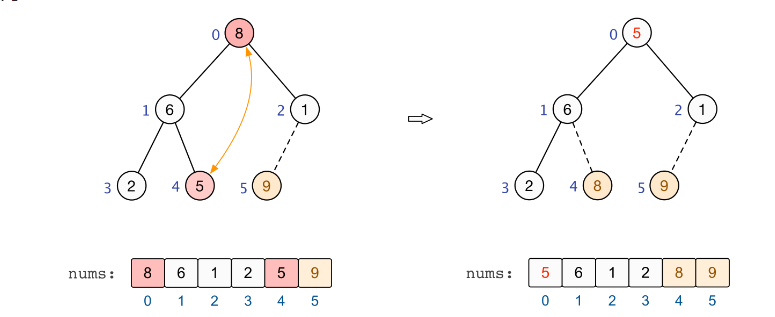
交换完成后，除去末尾最大元素，此时需要对堆进行重建，使得剩余元素继续满足大根堆的要求（省略）。

第三大元素：此时堆顶元素为待排序元素中的最大值（即原数组中的第三大值），将堆顶元素交换到末尾，如下所示：

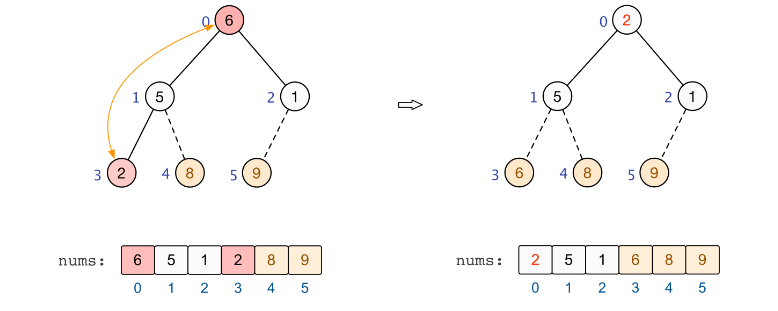
交换完成后，除去末尾最大元素，此时需要对堆进行重建，使得剩余元素继续满足大根堆的要求（省略）。

第四大元素：此时堆顶元素为待排序元素中的最大值（即原数组中的第四大值），将堆顶元素交换到末尾，如下所示：

交换完成后，除去末尾最大元素，此时需要对堆进行重建，使得剩余元素继续满足大根堆的要求（省略）。

次小元素（第五大元素）：此时堆顶元素为待排序元素中的最大值（即原数组中的次小元素或第五大元素），将堆顶元素交换到末尾，如下所示：

交换完成后，除去末尾最大元素，此时堆中仅剩一个元素，即为原数组中的最小值。

至此，基于大根堆的升序排列完成，如下所示：

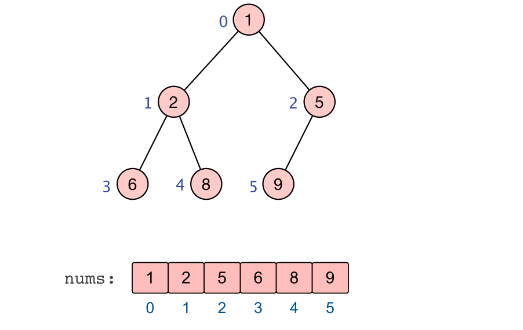
下面给出了 Python 语言的实现：

def Max_heap(li,low,high):#建立最大堆
    i = low
    j = 2 * i +1
    temp = li[low]
    while j < high :
        if li[j] < li[j+1] and j+1<high:
            j += 1
        if li[j] > li[i]:
            li[i],li[j] = li[j],li[i]
            i = j
            j = 2 * i + 1
        else :
            i = j
            j = 2 * i + 1
def heap_sort(li):#实现排序
    new_li=[]
    for j in range(n - 1, -1, -1):
        new_li.append(li[0])#记录最大元素
 
        li[j], li[0] = li[0], li[j]
 
 
        Max_heap(li,0,j-1)
 
        print(new_li)#每次记录都打印下来，也可以调整到后面打印最后结果
 
 
li = [2,4,1,6,8,2,7,9,3,10,5]
n = len(li)
for i in range(n//2-1, -1, -1):         # 从第一个非叶子节点n//2-1开始依次往上进行建堆的调整
            Max_heap(li, i, n-1)
 
heap_sort(li)