热门标签
热门文章
- 1关于我用iVX沉浸式体验了一把0代码创建飞机大战这件事_ivx项目实例
- 2UPF里面设置的power switch和powerswitch.tcl设置的power switch有什么区别?_addpowerswitch
- 3数电期末实验_)使用 8x2x2 个(串联每两个为一段)led 发光二极管,设计一个 2 位 8 段 led 数码
- 42024HW招募令!_hvv行动蓝队初级监测岗位薪资
- 5中文 NLP(8) -- 使用 CRF++ 和 BIO 表示法训练模型_bio 分词
- 62024年最新MySQL面试题总结,单点登录(Single-Sign-On)解决方案_关于单点登录的面试问题
- 7近十年苹果WWDC大会内容导读_历届wwdc内容
- 8Sql Server连接数据库(Windows模式及不用密码及用户名模式)
- 9c++ 重置stringstream的状态,清空stringstream,改变读写位置_stringstream 重置
- 10RabbitMQ 下载、安装_rabbitmq下载
当前位置: article > 正文
科研绘图(六)散点图矩阵
作者:小丑西瓜9 | 2024-06-12 03:31:26
赞
踩
散点图矩阵
散点图矩阵是一种显示多个变量之间关系的数据可视化工具,特别是当数据集包含三个或多个变量时,这种图表非常有用。这种图通常在探索性数据分析中使用,以便快速理解数据集中变量之间的关系。在散点图矩阵中,每行和每列都代表数据集中的一个变量,而矩阵中的每个小图(除了对角线)都是两个变量之间的散点图。
对角线图形:通常是每个变量的单变量分布。在您上传的图像中,这些是密度图,也可以是直方图或箱线图。它们提供了变量自身分布的视觉概览。
非对角线图形:这些是散点图,显示了数据集中每对变量间的关系。每个点代表数据集中的一个观测值。在您的图中,不同颜色的点代表
关键特征:
1、多变量关系展示:
对角线上方和下方的图是散点图,显示两个变量之间的关系。散点的分布可以揭示变量之间是否存在相关性,比如线性关系、非线性关系或没有明显关系。
2、分布可视化:
对角线上的图通常是直方图或密度图,显示单个变量的分布。这有助于了解数据的分布形状、集中趋势和离散程度。
3、数据分组:
不同的颜色或形状可以代表数据中的分类变量。
用途:
关系识别:快速识别多个变量间的潜在关系,比如线性、非线性或没有关系。
异常值检测:观察数据点集群之外的点来识别异常值。
分布检查:在对角线的图表帮助理解各个变量的分布特征。
群组比较:使用颜色或形状区分不同的群组,可以帮助比较不同群组的特征。
下面我们分别使用matlab以及python实现该种绘图。为了结果的准确性,我们使用国赛2017年C题的数据集进行绘制。
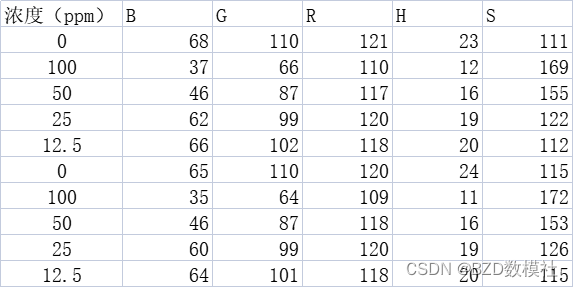
首先,利用python绘制这种散点图矩阵。如下所示

- import seaborn as sns
- import matplotlib.pyplot as plt
-
- # 创建数据框
- data = {
- '浓度(ppm)': [0, 100, 50, 25, 12.5, 0, 100, 50, 25, 12.5],
- 'B': [68, 37, 46, 62, 66, 65, 35, 46, 60, 64],
- 'G': [110, 66, 87, 99, 102, 110, 64, 87, 99, 101],
- 'R': [121, 110, 117, 120, 118, 120, 109, 118, 120, 118],
- 'H': [23, 12, 16, 19, 20, 24, 11, 16, 19, 20],
- 'S': [111, 169, 155, 122, 112, 115, 172, 153, 126, 115]
- }
-
- df = pd.DataFrame(data)
-
- # 使用Seaborn绘制散点矩阵图
- sns.set(style="ticks")
- sns.pairplot(df, diag_kind="kde", markers="o")
-
- # 显示图形
- plt.show()


- import pandas as pd
- import seaborn as sns
- import matplotlib.pyplot as plt
-
- # 创建数据框
- data = {
- '浓度(ppm)': [0, 100, 50, 25, 12.5, 0, 100, 50, 25, 12.5],
- 'B': [68, 37, 46, 62, 66, 65, 35, 46, 60, 64],
- 'G': [110, 66, 87, 99, 102, 110, 64, 87, 99, 101],
- 'R': [121, 110, 117, 120, 118, 120, 109, 118, 120, 118],
- 'H': [23, 12, 16, 19, 20, 24, 11, 16, 19, 20],
- 'S': [111, 169, 155, 122, 112, 115, 172, 153, 126, 115]
- }
- df = pd.DataFrame(data)
-
- # 定义数据列数量
- cols = df.columns
- n = len(cols)
-
- # 扩展颜色列表以匹配数据列的数量
- extended_colors = sns.color_palette("husl", n)
-
- # 设置更大的图表尺寸和字体大小
- plt.figure(figsize=(20, 20))
- plt.rcParams.update({'font.size': 10})
-
- for i in range(n):
- for j in range(n):
- ax = plt.subplot(n, n, i * n + j + 1)
-
- if i == j:
- sns.kdeplot(df[cols[i]], color=extended_colors[i], ax=ax)
- else:
- sns.scatterplot(x=cols[j], y=cols[i], data=df, color=extended_colors[j], ax=ax)
-
- # 设置坐标轴标签
- plt.xlabel(cols[j])
- plt.ylabel(cols[i])
-
- # 增加网格线
- plt.grid(True)
-
- # 增加整体标题和调整布局
- plt.suptitle("散点图矩阵 - 进一步美化版", fontsize=24)
- plt.subplots_adjust(top=0.95, hspace=0.4, wspace=0.4)
-
- # 显示图形
- plt.show()

为了进一步美化可视化,我们在每一张图中,都绘制了线性回归的拟合图如下所示。

下面是matlab绘图代码 
- % 创建数据矩阵
- data = [
- 0 68 110 121 23 111
- 100 37 66 110 12 169
- 50 46 87 117 16 155
- 25 62 99 120 19 122
- 12.5 66 102 118 20 112
- 0 65 110 120 24 115
- 100 35 64 109 11 172
- 50 46 87 118 16 153
- 25 60 99 120 19 126
- 12.5 64 101 118 20 115
- ];
-
- % 创建变量名
- varNames = {'浓度 (ppm)', 'B', 'G', 'R', 'H', 'S'};
-
- % 创建数据表格
- dataTable = array2table(data, 'VariableNames', varNames);
-
- % 绘制散点矩阵图
- figure;
- gplotmatrix(dataTable{:,:}, [], [], [], [], [], false);
-
- % 添加标签和标题
- xlabel('X轴标签');
- ylabel('Y轴标签');
- title('散点矩阵图');
-
- % 调整坐标轴范围
- xlim([min(data(:)) max(data(:))]);
- ylim([min(data(:)) max(data(:))]);
- % 自定义图例
- legend({'类别1', '类别2', '类别3'});
-
- % 调整图的尺寸
- set(gcf, 'Position', [100, 100, 800, 600]); % 设置图的位置和大小


- % 创建数据矩阵
- data = [
- 0 68 110 121 23 111
- 100 37 66 110 12 169
- 50 46 87 117 16 155
- 25 62 99 120 19 122
- 12.5 66 102 118 20 112
- 0 65 110 120 24 115
- 100 35 64 109 11 172
- 50 46 87 118 16 153
- 25 60 99 120 19 126
- 12.5 64 101 118 20 115
- ];
-
- % 创建变量名
- varNames = {'浓度 (ppm)', 'B', 'G', 'R', 'H', 'S'};
-
- % 创建数据矩阵和变量名
- % ... [数据和变量名的代码] ...
-
- % 创建数据表格
- dataTable = array2table(data, 'VariableNames', varNames);
-
- % 绘制散点矩阵图
- figure;
- colors = lines(size(data, 2)); % 使用 lines 颜色图
- markerShapes = {'+', 'o', '*', '.', 'x', 's', 'd', '^', 'v', '>'}; % 标记形状
- [h, ax] = gplotmatrix(dataTable{:,:}, [], [], colors, markerShapes, 12, 'on', 'hist', varNames, varNames);
-
- % 美化轴标签和标题
- set(ax, 'FontSize', 12, 'FontWeight', 'Bold');
- title('散点矩阵图', 'FontSize', 16, 'FontWeight', 'Bold');
- xlabel('X轴标签', 'FontSize', 14);
- ylabel('Y轴标签', 'FontSize', 14);
-
- % 添加网格线
- set(ax, 'XGrid', 'on', 'YGrid', 'on');
-
- % 调整子图间的间距
- set(ax, 'XTickLabelRotation', 45, 'YTickLabelRotation', 45);
-
- % 改进颜色映射
- colormap('jet');
-
- % 添加颜色说明标签
- for i = 1:length(varNames)
- annotation('textbox', [.85, 1 - 0.05*i, .1, .05], 'String', varNames{i}, 'Color', colors(i,:), 'EdgeColor', 'none');
- end
-
- % 保存图像
- saveas(gcf, '散点矩阵图_改进版.png');

最后,我们尝试在每一个图中加入线性回归的拟合图,如下所示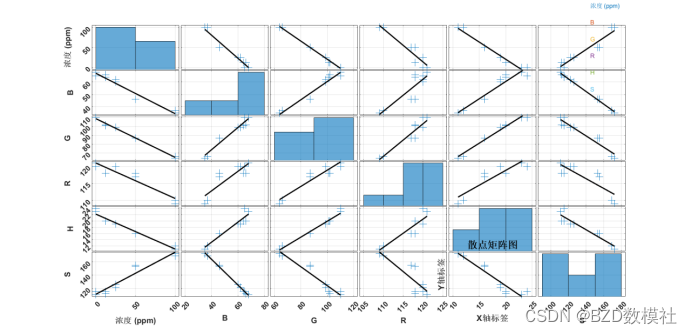
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/小丑西瓜9/article/detail/706097
推荐阅读
相关标签


