机器学习算法之Apriori算法（python实现）_apriori算法python代码

        Apriori算法是一种经典的关联规则挖掘算法，用于从大规模数据集中发现频繁项集及其关联规则。
        Apriori算法基于以下两个重要概念：支持度（support）和置信度（confidence）。

        支持度衡量一个项集在数据集中出现的频率，定义为包含该项集的事务数目与总事务数的比例。置信度衡量关联规则的可靠性，定义为规则的支持度与规则左侧项集的支持度的比值。

        Apriori算法的主要思想是利用频繁项集的性质，通过逐层搜索的方式发现频繁项集。算法的过程如下：

        1.初始扫描：计算单个项的支持度，筛选出满足最小支持度阈值的项集作为一阶频繁项集。
        2.迭代生成：根据当前的k-1阶频繁项集，生成候选k阶项集。
        3.连接：将k-1阶频繁项集两两连接生成候选k阶项集。
        4. 剪枝：对候选k阶项集进行剪枝操作，删除包含非频繁子项集的项集。
        5.频繁项集计数：对候选k阶项集进行扫描，计算每个项集的支持度。
        6.停止条件：如果没有发现新的频繁项集，或者已达到预定的阶数，则停止迭代。

        Apriori算法通过逐层搜索的方式逐渐生成更高阶的频繁项集，直到不能再生成新的频繁项集为止。最后，基于频繁项集，可以计算关联规则的置信度。

        本次算法代码中我选用的是一组购物商品数据，通过Apriori算法来找出这些商品中有哪些商品之间存在关联。

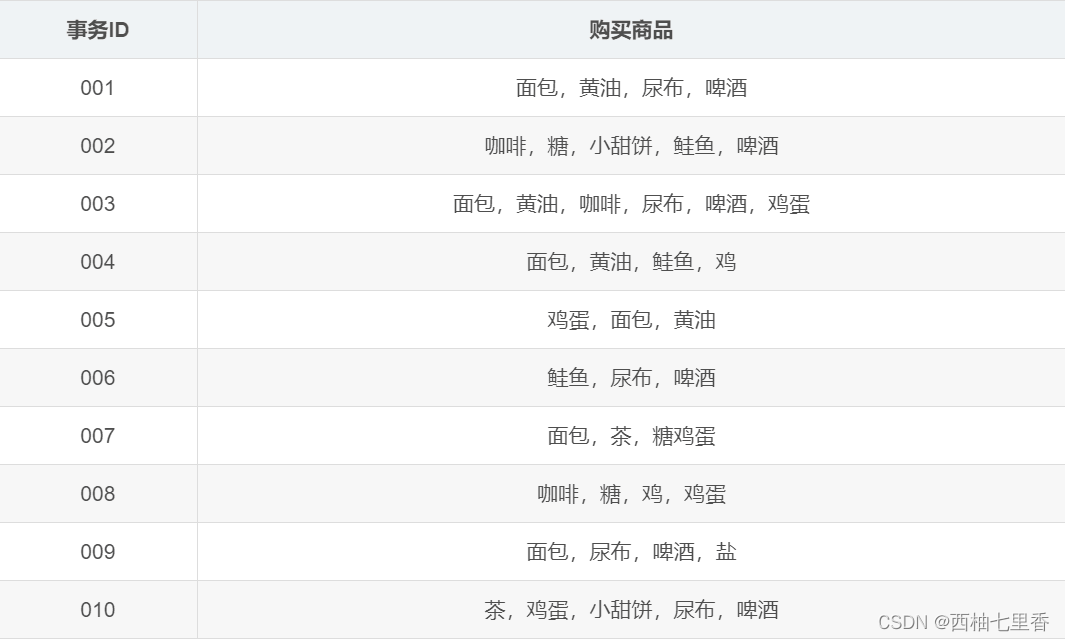
        具体的python代码如下：

# 数据集为一组购物篮数据
dataset = {
    '1': {'面包', '黄油', '尿布', '啤酒'},
    '2': {'咖啡', '糖', '小甜饼', '鲑鱼', '啤酒'},
    '3': {'面包', '黄油', '咖啡', '尿布', '啤酒', '鸡蛋'},
    '4': {'面包', '黄油', '鲑鱼', '鸡'},
    '5': {'鸡蛋', '面包', '黄油'},
    '6': {'鲑鱼', '尿布', '啤酒'},
    '7': {'面包', '茶', '糖鸡蛋'},
    '8': {'咖啡', '糖', '鸡', '鸡蛋'},
    '9': {'面包', '尿布', '啤酒', '盐'},
    '10': {'茶', '鸡蛋', '小甜饼', '尿布', '啤酒'}
}
 
support = 4  # 设置最小支持度计数 = 4
k = 0  # k表示当前为频繁k项集
 
goods = set()  # 用集合goods保存所有的商品
 
for i in dataset:
    for item in dataset[i]:
        goods.add(item)
 
frequent = list()  # 用列表frequent保存每一次的频繁项集
appear = list()  # 用列表appear记录频繁项集中每项出现的次数
 
# 求频繁1项集
k += 1
for item in goods:
    times = 0  # 用times记录每个商品出现在购物篮数据的次数
    for i in dataset:
        if item in dataset[i]:
            times += 1
    if times >= support:  # 若次数大于最小支持度计数，则添加到频繁1项集中
        appear.append(times)
        temp = set()
        temp.add(item)
        frequent.append(temp)
 
last = frequent  # 用列表last记录上一次迭代的频繁项集
frequent = list()
appear = list()
 
# 求频繁2项集，即频繁1项集中的数据两两求并集，若该并集出现在购物篮数据中的次数
# 大于最小支持度计数，则添加到频繁2项集中
k += 1
for i in range(0, len(last) - 1):
    for j in range(i + 1, len(last)):
        times = 0
        temp = last[i] | last[j]
        for item in dataset:
            if temp & dataset[item] == temp:
                times += 1
        if times >= support:
            appear.append(times)
            frequent.append(temp)
 
last = frequent  # 用列表last记录上一次迭代的频繁项集
appear2 = appear  # 用列表last记录上一次迭代的频繁项集中每项出现的次数
 
# 求之后每次迭代后的频繁项集，以频繁3项集为例，频繁2项集中的数据两两求并集
# 若该并集刚好包含3个商品且出现在购物篮数据中的次数大于最小支持度计数，则添加到频繁3项集中
while (True):
    if len(frequent) <= 1:
        break
 
    frequent = list()
    appear = list()
    k += 1
 
    for i in range(0, len(last) - 1):
        for j in range(i + 1, len(last)):
            times = 0
            temp = last[i] | last[j]
            if last[i] & last[j] != set() and len(temp) == k:
                for item in dataset:
                    if temp & dataset[item] == temp:
                        times += 1
                if times >= support and temp not in frequent:  # 由于频繁项集用列表保存，因此此处需要进行去重
                    appear.append(times)
                    frequent.append(temp)
 
    if len(frequent) >= 1:
        last = frequent
        appear2 = appear
 
print('\n关联规则\t\t 支持度计数')
for i in range(0, len(last)):
    print(last[i], '\t', appear2[i])
print()
 
# 计算每个关联规则的置信度
print('X\t\t Y\t 置信度')
 
result = set()
 
for i in range(0, len(last)):
    for item in last[i]:
 
        temp = set()
 
        for j in last[i]:
            temp.add(j)
 
        temp.discard(item)
 
        times = 0
        for item2 in dataset:
            if temp & dataset[item2] == temp:
                times += 1
 
        print(temp, '\t', item, '\t', appear2[i] / times)

        代码运行结果如下：