移动机器人MPC控制仿真实现_mpc模型是怎么控制移动机器人呢

0 运动学建模

首先建立移动机器人运动学方程：
[ x ˙ y ˙ θ ˙ ] = [ c o s θ 0 s i n θ 0 0 1 ] [ v ω ]

$$\begin{bmatrix} \dot{x} \\ \dot{y} \\ \dot{\theta} \end{bmatrix}$$ = $$\begin{bmatrix} cos\theta && 0\\ sin\theta && 0\\ 0 && 1 \end{bmatrix}$$ $$\begin{bmatrix} v\\ \omega \end{bmatrix}$$ ⎣⎡​x˙y˙​θ˙​⎦⎤​=⎣⎡​cosθsinθ0​​001​⎦⎤​[vω​]
其中，$P=\left[\begin{array}{c}x\\ y\\ \theta \end{array}\right]$为机器人全局坐标系下的位姿，$u=\left[\begin{array}{c}v\\ \omega \end{array}\right]$为机器人的线速度和角速，是系统的控制输入，暂时不把左右轮转速引入。

移动机器人跟踪问题中输入为参考轨迹$P_r$和参考速度$u_r$。

这里MPC模型的状态量有多种选择：1）全局坐标系位姿；2）全局坐标系误差；3）局部坐标系误差（即全局误差投影到局部坐标系）。下面来一一建模分析。

1 局部误差为状态量

1.1 MPC建模

首先以局部误差为状态量进行分析，对于移动机器人的非完整性，存在以下假设：机器人不发生侧向滑动，即在全局坐标系下${\dot{y}}_L=0$，即有：
x ˙ s i n θ − y ˙ c o s θ = 0 x ˙ c o s θ + y ˙ s i n θ = v

$$\begin{aligned} \dot{x}sin\theta - \dot{y}cos\theta &=0 \\ \dot x cos\theta+\dot ysin\theta &= v \end{aligned}$$ x˙sinθ−y˙​cosθx˙cosθ+y˙​sinθ​=0=v​

此公式对于参考位姿和参考速度依然成立。

定义机器人局部坐标系下位姿误差为：
[ x e y e θ e ] = [ c o s θ s i n θ 0 − s i n θ c o s θ 0 0 0 1 ] [ x r − x y r − y θ r − θ ]

$$\begin{bmatrix} x_e \\ y_e \\ \theta _e \end{bmatrix}$$ = $$\begin{bmatrix} cos\theta && sin\theta && 0 \\ -sin\theta && cos\theta && 0\\ 0 && 0 && 1 \end{bmatrix}$$ $$\begin{bmatrix} x_r-x \\ y_r-y \\ \theta _r-\theta \end{bmatrix}$$ ⎣⎡​xe​ye​θe​​⎦⎤​=⎣⎡​cosθ−sinθ0​​sinθcosθ0​​001​⎦⎤​⎣⎡​xr​−xyr​−yθr​−θ​⎦⎤​
则有：
$$\begin{array}{rl}{\dot{x}}_e& =-\omega sin\theta (x_r-x)+\omega cos\theta (y_r-y)+cos\theta ({\dot{x}}_r-\dot{x})+sin\theta ({\dot{y}}_r-\dot{y})\\ & =\omega y_e-v+{\dot{x}}_{r}cos\theta +{\dot{y}}_{r}sin\theta (由于\theta \ne {\theta }_r，后两项不能合并为v_r)\\ & =\omega y_e-v+{\dot{x}}_{r}cos({\theta }_r-{\theta }_e)+{\dot{y}}_{r}sin({\theta }_r-{\theta }_e)\\ & =\omega y_e-v+{\dot{x}}_r(cos{\theta }_{r}cos{\theta }_e+sin{\theta }_{r}sin{\theta }_e)+{\dot{y}}_r(sin{\theta }_{r}cos{\theta }_e-cos{\theta }_{r}sin{\theta }_e)\\ & =\omega y_e-v+({\dot{x}}_{r}cos{\theta }_r+{\dot{y}}_{r}sin{\theta }_r)cos{\theta }_e+({\dot{x}}_{r}sin{\theta }_r-{\dot{y}}_{r}cos{\theta }_r)sin{\theta }_e\\ & =\omega y_e-v+v_{r}cos{\theta }_e\\ {\dot{y}}_e& =-\omega cos\theta (x_r-x)-\omega sin\theta (y_r-y)-sin\theta ({\dot{x}}_r-\dot{x})+cos\theta ({\dot{y}}_r-\dot{y})\\ & =-\omega x_e-{\dot{x}}_{r}sin\theta +{\dot{y}}_{r}cos\theta \\ & =-\omega x_e-{\dot{x}}_{r}sin({\theta }_r-{\theta }_e)+{\dot{y}}_{r}cos({\theta }_r-{\theta }_e)\\ & =-\omega x_e-{\dot{x}}_r(sin{\theta }_{r}cos{\theta }_e-cos{\theta }_{r}sin{\theta }_e)+{\dot{y}}_r(cos{\theta }_{r}cos{\theta }_e+sin{\theta }_{r}sin{\theta }_e)\\ & =-\omega x_e+(-{\dot{x}}_{r}sin{\theta }_r+{\dot{y}}_{r}cos{\theta }_r)cos{\theta }_e+({\dot{x}}_{r}cos{\theta }_r+{\dot{y}}_{r}sin{\theta }_r)sin{\theta }_e\\ & =-\omega x_e+v_{r}sin{\theta }_e\\ {\dot{\theta }}_e& ={\dot{\theta }}_r-\dot{\theta }={\omega }_r-\omega \end{array}$$

写成矩阵形式为：
[ x ˙ e y ˙ e θ ˙ e ] = [ ω y e − v + v r c o s θ e − ω x e + v r s i n θ e ω r − ω ] (1)

$$\begin{aligned} \begin{bmatrix} \dot x_e \\ \dot y_e \\ \dot \theta_e \end{bmatrix} = \begin{bmatrix} \omega y_e - v + v_rcos\theta_e\\ -\omega x_e +v_rsin\theta_e \\ \omega_r - \omega \end{bmatrix} \end{aligned}$$ \tag{1} ⎣⎡​x˙e​y˙​e​θ˙e​​⎦⎤​=⎣⎡​ωye​−v+vr​cosθe​−ωxe​+vr​sinθe​ωr​−ω​⎦⎤​​(1)

很明显上式是一个非线性系统，需要进行线性化：
[ x ˙ e y ˙ e θ ˙ e ] = [ 0 ω 0 − ω 0 0 0 0 0 ] [ x e y e θ e ] + [ − v + v r c o s θ e v r s i n θ e ω r − ω ]

$$\begin{aligned} \begin{bmatrix} \dot x_e \\ \dot y_e \\ \dot \theta_e \end{bmatrix} = \begin{bmatrix}0 && \omega && 0 \\ -\omega && 0 && 0 \\ 0 && 0 && 0 \end{bmatrix} \begin{bmatrix} x_e \\ y_e \\ \theta_e \end{bmatrix}+ \begin{bmatrix}-v+v_rcos\theta_e \\ v_r sin\theta_e\\ \omega_r - \omega \end{bmatrix} \end{aligned}$$ ⎣⎡​x˙e​y˙​e​θ˙e​​⎦⎤​=⎣⎡​0−ω0​​ω00​​000​⎦⎤​⎣⎡​xe​ye​θe​​⎦⎤​+⎣⎡​−v+vr​cosθe​vr​sinθe​ωr​−ω​⎦⎤​​
由于$\underset{{\theta }_e\to 0}{\lim }cos{\theta }_e=1,\underset{{\theta }_e\to 0}{\lim }sin{\theta }_e={\theta }_e$，上式可写成：
$$\begin{array}{rl}\left[\begin{array}{c}{\dot{x}}_e\\ {\dot{y}}_e\\ {\dot{\theta }}_e\end{array}\right]& =\left[\begin{array}{ccccc}0& & \omega & & 0\\ -\omega & & 0& & v_r\\ 0& & 0& & 0\end{array}\right]\left[\begin{array}{c}{x}_e\\ y_e\\ {\theta }_e\end{array}\right]+\left[\begin{array}{c}{v}_r-v\\ 0\\ {\omega }_r-\omega \end{array}\right]\\ & =\left[\begin{array}{ccccc}0& & \omega & & 0\\ -\omega & & 0& & v_r\\ 0& & 0& & 0\end{array}\right]\left[\begin{array}{c}{x}_e\\ y_e\\ {\theta }_e\end{array}\right]+\left[\begin{array}{ccc}1& & 0\\ 0& & 0\\ 0& & 1\end{array}\right]\left[\begin{array}{c}{v}_r-v\\ {\omega }_r-\omega \end{array}\right]\end{array}$$

此时定义MPC系统状态量为 X = [ x e y e θ e ] X=

$$\begin{bmatrix}x_e \\y_e \\\theta_e\end{bmatrix}$$ X=⎣⎡​xe​ye​θe​​⎦⎤​，控制量为$\tilde{u}=\left[\begin{array}{c}{v}_r-v\\ {\omega }_r-\omega \end{array}\right]$，$\tilde{u}=u_r-u$。

令 A = [ 0 ω 0 − ω 0 v r 0 0 0 ] ,   B = [ 1 0 0 0 0 1 ] A=

$$\begin{bmatrix}0 && \omega && 0 \\ -\omega && 0 && v_r \\ 0 && 0 && 0\end{bmatrix}$$ ,\ B= $$\begin{bmatrix}1 && 0 \\0 && 0\\0 && 1\end{bmatrix}$$ A=⎣⎡​0−ω0​​ω00​​0vr​0​⎦⎤​, B=⎣⎡​100​​001​⎦⎤​，则有：
$$\dot{X}=AX+B\tilde{u}$$

离散化：
X ( k + 1 ) − X ( k ) Δ T = A X ( k ) + B u ~ ( k )

$$\begin{aligned} \frac{X(k+1)-X(k)}{\Delta T}=AX(k)+B\widetilde u(k) \end{aligned}$$ ΔTX(k+1)−X(k)​=AX(k)+Bu (k)​
其中$\Delta T$为离散时间间隔，即：
$$\begin{array}{r}X(k+1)=(I+\Delta T)AX(k)+\Delta TB\tilde{u}(k)\end{array}$$
令$\tilde{A}=(I+\Delta T)A,\tilde{B}=\Delta TB$，同时设定预测时域为$N$，则有：
$$\begin{array}{rl}X(k+1)& =\tilde{A}X(k)+\tilde{B}\tilde{u}(k)\\ X(k+2)& =\tilde{A}X(k+1)+\tilde{B}\tilde{u}(k+1)={\tilde{A}}^{2}X(k)+\tilde{A}\tilde{B}\tilde{u}(k)+\tilde{B}\tilde{u}(k+1)\\ X(k+3)& ={\tilde{A}}^{3}X(k)+{\tilde{A}}^2\tilde{B}\tilde{u}(k)+\tilde{A}\tilde{B}\tilde{u}(k+1)+\tilde{B}\tilde{u}(k+2)\\ ...& \\ X(k+N)& ={\tilde{A}}^{N}X(k)+\sum _{i=0}^{N-1}{\tilde{A}}^{N-i-1}\tilde{B}\tilde{u}(k+i)\end{array}$$
这里其实做了简化，根据$A$的表达式，$\tilde{A}(k)$和$\tilde{A}(k+1)$不完全等价。

令：
Y ( k ) = [ X ( k + 1 ) X ( k + 2 ) . . . X ( k + N ) ] , Ψ = [ A ~ A ~ 2 . . . A ~ N ] , Δ U = [ u ~ ( k ) u ~ ( k + 1 ) . . . u ~ ( k + N − 1 ) ] Θ = [ B ~ 0 . . . 0 A ~ B ~ B ~ . . . 0 . . . A ~ N − 1 B ~ A ~ N − 2 B ~ . . . B ~ ] Y(k)=

$$\begin{bmatrix}X(k+1)\\ X(k+2)\\ ...\\X(k+N)\end{bmatrix}$$ , \Psi= $$\begin{bmatrix}\widetilde A\\ \widetilde A^2\\ ...\\\widetilde A^N\end{bmatrix}$$ , \Delta U= $$\begin{bmatrix}\widetilde u(k)\\ \widetilde u(k+1)\\ ...\\\widetilde u(k+N-1)\end{bmatrix}$$ \\ \Theta = $$\begin{bmatrix} \widetilde B && 0 && ... && 0 \\ \widetilde A\widetilde B && \widetilde B && ... && 0 \\ ...\\ \widetilde A^{N-1}\widetilde B && \widetilde A^{N-2}\widetilde B && ... && \widetilde B \end{bmatrix}$$ Y(k)=⎣⎢⎢⎡​X(k+1)X(k+2)...X(k+N)​⎦⎥⎥⎤​,Ψ=⎣⎢⎢⎡​A A 2...A N​⎦⎥⎥⎤​,ΔU=⎣⎢⎢⎡​u (k)u (k+1)...u (k+N−1)​⎦⎥⎥⎤​Θ=⎣⎢⎢⎡​B A B ...A N−1B ​​0B A N−2B ​​.........​​00B ​⎦⎥⎥⎤​
则有：
$$Y(k)=\Psi X(k)+\Theta \Delta U$$
其中$Y(k)$为$k$时刻预测时域内的误差，定义代价函数：
$$\begin{array}{rl}J& =Y^T(k)QY(k)+\Delta U^{T}R\Delta U\end{array}$$
其中$Q$和$R$为权重。该代价函数可以使预测时域内误差最小，且对控制量也有一定约束。对$J$作展开：
$$\begin{array}{rl}J& =(\Psi X(k)+\Theta \Delta U{)}^{T}Q(\Psi X(k)+\Theta \Delta U)+\Delta U^{T}R\Delta U\\ & =X^T(k){\Psi }^{T}Q\Psi X(k)+2X^T(k){\Psi }^{T}Q\Theta \Delta U+\Delta U^T{\Theta }^{T}Q\Theta \Delta U+\Delta U^{T}R\Delta U\\ & =\Delta U^T({\Theta }^{T}Q\Theta +R)\Delta U+2X^T(k){\Psi }^{T}Q\Theta \Delta U+X^T(k){\Psi }^{T}Q\Psi X(k)\end{array}$$
由于在$k$时刻，$X(k),\Psi ,\Theta$均为确定值，所以上式即为关于$\Delta U$的二次型。

令
$$H=2({\Theta }^{T}Q\Theta +R),f^T=2X^T(k){\Psi }^{T}Q\Theta$$
即可利用MATLAB中quadprog函数求解。

在得到$\Delta U^{\ast }$后，取其中第一个元素${\tilde{u}}^{\ast }(k)$作为$k$时刻的MPC系统控制量，则实际速度控制量为：
$$u^{\ast }(k)=u_r(k)-{\tilde{u}}^{\ast }(k)$$

1.2 仿真实现参考代码

clear;clc;
close all;

%% 仿真参数设定
dt = 0.01;                  % 离散时间间隔
num_step = 2000;            % 仿真步数
t = (0:num_step-1)*dt;      % 生成仿真时间序列

%% 运动学参数设定（本实例给定参考速度）
u_r = [1;0.5]*ones(1,num_step);                 % 参考速度（圆轨迹）
% u_r = [3;0]*ones(1,num_step);                   % 参考速度（直线轨迹）

% 利用积分法生成参考轨迹
P_r = zeros(3,num_step);
for k = 2:num_step
    last_theta = P_r(3,k-1);
    P_r(:,k) = P_r(:,k-1)+[cos(last_theta),0;sin(last_theta),0;0,1]*u_r(:,k-1)*dt;
end

% 设定初始位置和初始速度
P = [1;-1;0];               % 初始位置
u = [0;0];                  % 初始速度
X = zeros(3,num_step);      % 存储误差向量 

%% MPC控制器参数设定
N = 10;                     % 预测时序长度
Q = 5*diag([4,10,0.1]);     % 状态量权重
R = 1*diag([1,0.5]);        % 控制量权重
Q_ = kron(eye(N),Q);        % 利用K积将权重矩阵扩充到与Y相同维度
R_ = kron(eye(N),R);
B = [1,0;0,0;0,1];          % B 矩阵
B_ = dt*B;                  % B~ 矩阵

%% 二次型求解器设置（使用 interior-point-convex 算法，不显示迭代过程）
options = optimoptions('quadprog',...
    'Algorithm','interior-point-convex','Display','off');

%% 滚动优化 （为了不处理最后N个时刻的特殊情况，循环只进行到 num_step-N ）
tic;
figure(1);
hold on;
xlabel('x(m)');
ylabel('y(m)');
for k = 1:num_step-N
    % 刻画每个时刻的参考位置和实际位置
    plot(P(1,k),P(2,k),'b.');
    plot(P_r(1,k),P_r(2,k),'r.');
    drawnow;
    
    % 计算当前时刻的 X
    Tx = [cos(P(3,k)),sin(P(3,k)),0;
        -sin(P(3,k)),cos(P(3,k)),0;
        0,0,1];
    X(:,k) = Tx*(P_r(:,k)-P(:,k));
    
    % 计算当前时刻的 \Psi 和 \Theta
    A = [0,u(2,k),0;-u(2,k),0,u_r(1,k);0,0,0];      % A 矩阵
    A_ = eye(size(P,1))+dt*A;         % A_ 矩阵
    Psi = zeros(3*N,3);                 % 初始化 \Psi
    Theta = zeros(3*N,2*N);             % 初始化 \Theta
    for j = 1:N
        Psi(3*j-2:3*j,1:3) = A_^j;      % \Psi 的第j块
        for i = 1:j
            Theta(3*j-2:3*j,2*i-1:2*i) = A_^(j-i)*B_;   % \Theta 的第(j,i)块
        end
    end
    
    % 计算 H 和 f
    H = 2*(Theta'*Q_*Theta+R_);
    f = (2*X(:,k)'*Psi'*Q_*Theta)';
    
    % 调用 quadprog 求解器
    [U_star,fval,exitflag,output,lambda] = quadprog(H,f,[],[],[],[],[],[],[],options);
    
    % 输入控制量利用积分计算下一个位姿和误差
    u_star = U_star(1:2);           % 取出 U 的第一部分（前两项）   
    u =[u, u_r(:,k) - u_star];      % 计算实际线速度和角速度控制量
    last_theta = P(3,k);
    P =[P, P(:,k)+[cos(last_theta),0;sin(last_theta),0;0,1]*u(:,k+1)*dt];
end
toc;

%% 误差收敛速度
mse = sqrt(sum((X.^2),1));
figure;
plot(t(1:num_step-N),mse(1:num_step-N),'b-','LineWidth',1)
xlabel('t(s)');
ylabel('mse');

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

直线跟踪效果：

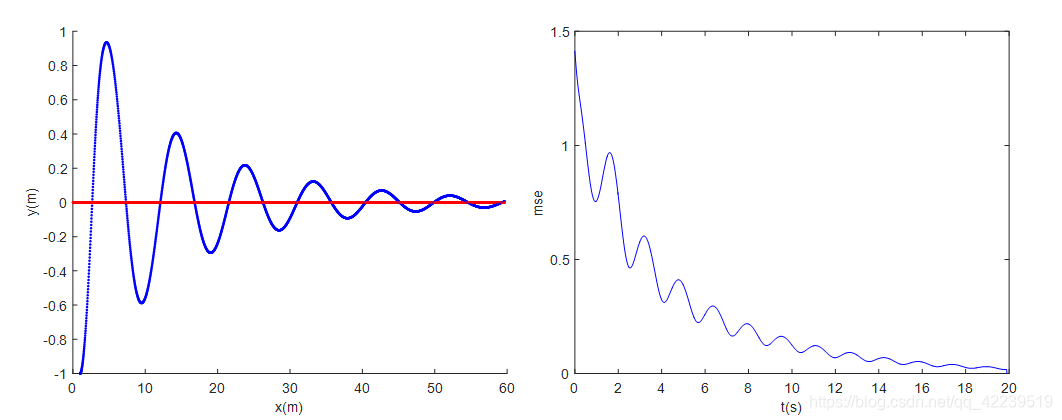
圆轨迹跟踪效果：

1.3结果分析

可以看到收敛速度较慢，有可能是权重影响的，可以自行修改参数进行仿真。另外还可以在quadprog求解器中加入控制量的约束，使其不要产生过大的加速度。

2 全局坐标系为状态量

3 全局误差为状态量