寸_铁

这个屌丝很懒，什么也没留下！

热门标签

程序员常用 10 种算法_程序算法

作者：寸_铁 | 2024-06-29 23:02:39

踩

程序算法

二分查找算法(非递归)

代码实现：

package com.atguigu.binarysearch;

/**
 * @ClassName BinarySearchDemo
 * @Author Jeri
 * @Date 2022-02-28 20:39
 * @Description 非递归的二分查找算法
 */

public class BinarySearchDemo {

    /*
     * @Description 二分查找非递归
     * @Date 2022/2/28 20:45
     * @param arr 带查找的数组 默认为升序
     * @param target 待查找的数值
     * @return 对应下标 -1 表示没有找到
     */
    public static int binarySearch(int[] arr,int target){
        int left = 0;
        int right = arr.length - 1;

        if(target < arr[left] || target > arr[right]){
            return -1;
        }

        while (left <= right){
            int mid = (left + right) / 2;
            int midValue = arr[mid];
            if(midValue == target){
                return mid;
            }else if(midValue > target){
                //向左查找
                right = mid - 1;
            }else{
                //向右查找
                left = mid + 1;
            }
        }

        return -1;
    }

    public static void main(String[] args) {
        int[] arr = {1,3, 8, 10, 11, 67, 100};
        int index = binarySearch(arr, 100);
        System.out.println("index=" + index);//
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

index=6
1

分治算法

基本介绍

分治法是一种很重要的算法。字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础，如排序算法(快速排序，归并排序)，傅立叶变换(快速傅立叶变换)……

分治算法可以求解的一些经典问题：二分搜索大整数乘法棋盘覆盖合并排序快速排序线性时间选择最接近点对问题循环赛日程表 汉诺塔

基本步骤

分治法在每一层递归上都有三个步骤：

分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题
解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题
合并：将各个子问题的解合并为原问题的解

在这里插入图片描述

汉诺塔

汉诺塔：汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着 64 片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘

思路分析：

如果是有一个盘，A – > C

如果我们有 n >= 2 情况，我们总是可以看做是两个盘 1.最下边的盘 2. 上面的盘

先把最上面的盘 A – > B
把最下面的盘 A --> C
把B塔上的所有盘 B --> C

代码实现：

package com.atguigu.dac;

import sun.applet.Main;

/**
 * @ClassName HanoitowerDemo
 * @Author Jeri
 * @Date 2022-03-01 10:02
 * @Description 汉诺塔问题
 */
public class HanoitowerDemo {

    //汉诺塔移动 使用分治算法
    // a 起始  c 目标 b 辅助
    public static void hanoiTower(int num,char a,char b,char c){
        //如果只有一个盘
        if(num == 1){
            // A--> C
            System.out.println("第1个盘从" + a + "-->" + c);
        }else {
            //盘的数量 >= 2
            //最上面的盘 A-->B
            hanoiTower(num - 1, a, c, b);
            //最下面的盘 A-->C
            System.out.println("第" + num + "个盘从" + a + "-->" + c);
            //B塔上所有盘 从B-->C
            hanoiTower(num - 1, b, a, c);
        }
    }

    public static void main(String[] args) {
        hanoiTower(3,'A','B','C');
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

第1个盘从A-->C
第2个盘从A-->B
第1个盘从C-->B
第3个盘从A-->C
第1个盘从B-->A
第2个盘从B-->C
第1个盘从A-->C
1
2
3
4
5
6
7

动态规划

应用场景 01背包

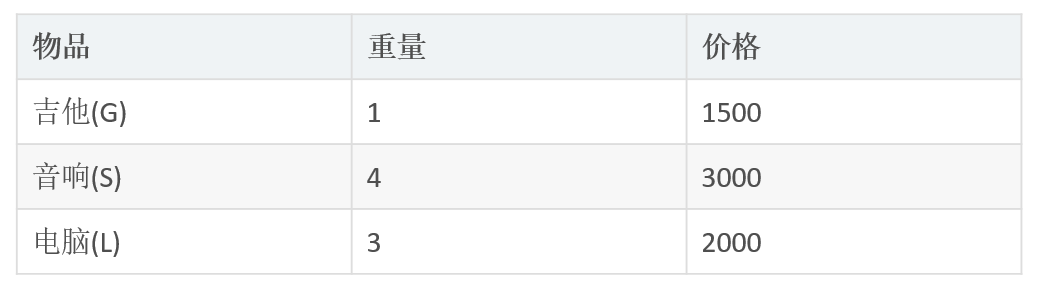
背包问题：有一个背包，容量为 4 磅，现有如下物品

要求达到的目标为装入的背包的总价值最大，并且重量不超出
要求装入的物品不能重复

在这里插入图片描述

算法介绍

动态规划 (Dynamic Programming) 算法的核心思想：将大问题划分为小问题进行解决，从而一步步获得最优解的处理算法
动态规划算法与分治算法类似，基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原始问题的解
动态规划求解问题的特点，经分解得到子问题往往不是相互独立的。(下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解)
动态规划可以通过填表的方式来逐步推进，得到最优解

01背包思路分析

背包问题主要是指一个给定容量的背包、若干具有一定价值和重量的物品，如何选择物品放入背包使物品的价值最大。其中又分 01 背包和完全背包(完全背包指的是：每种物品都有无限件可用)

这里的问题属于 01 背包，即每个物品最多放一个。而无限背包可以转化为 01 背包。

算法的主要思想，利用动态规划来解决。每次遍历到的第 i 个物品，根据 w[i]和 val[i]来确定是否需要将该物品放入背包中。即对于给定的 n 个物品，设 val[i]、w[i]分别为第 i 个物品的价值和重量，C 为背包的容量。再令 v[i][j]表示在前 i 个物品中能够装入容量为 j 的背包中的最大价值。则我们有下面的结果：

v[i][0]=v[0][j]=0; //表示填入表第一行和第一列是 0
当 w[i]> j 时：v[i][j]=v[i-1][j] // 当准备加入新增的商品的容量 > 当前背包的容量时，就直接使用上一个单元格的装入策略
当 w[i] <= j 时： v[i][j]=max{v[i-1][j], val[i]+v[i-1][j-w[i]]}

代码实现

package com.atguigu.dp;

/**
 * @ClassName Backpack01
 * @Author Jeri
 * @Date 2022-03-02 20:33
 * @Description 使用dp解决01背包
 */
public class Backpack01 {
    public static void main(String[] args) {
        //物品重量
        int[] w = {1,4,3};
        //物品的价值
        int[] val = {1500,3000,2000};

        int m = 4;//背包容量
        int n = val.length;//可选物品总数

        //创建二维数组 v[n+1][m+1]
        //v[i][j] 表示在前 i 个物品中能够装入容量为 j 的背包中的最大价值
        int[][] v = new int[n+1][m+1];
        //记录放入商品的情况
        int[][] path = new int[n+1][m+1];

        //初始化第一行和第一列
        for(int i = 0;i < v.length;i++){
            v[i][0] = 0;
        }

        for(int i = 0;i < v[0].length;i++){
            v[0][i] = 0;
        }

        //根据思路的公式进行动态规划分析
        for(int i = 1;i < v.length;i++){
            //i 控制 第i个物品
            for(int j = 1;j < v[0].length;j++){
                //j表示当前背包容量
                if(w[i - 1] > j){
                    v[i][j] = v[i - 1][j];
                }else{
                    if(v[i - 1][j] < val[i - 1] + v[i - 1][j - w[i - 1]]){
                        v[i][j] = val[i - 1] + v[i - 1][j - w[i - 1]];
                        //记录添加物品的情况
                        path[i][j] = 1;
                    }else{
                        v[i][j] = v[i - 1][j];
                    }
                }
            }
        }

        //查看 二维数组 v
        for(int i = 0;i < v.length;i++){
            for(int j = 0;j < v[0].length;j++){
                System.out.print(v[i][j] + "\t");
            }
            System.out.println();
        }

        //查看哪些物品放入背包
        int i = path.length - 1;
        int j = path[0].length - 1;
        while (i > 0 && j > 0){
            if(path[i][j] == 1){
                System.out.printf("第%d个商品放入背包\n",i);
                j -= w[i-1];
            }
            i --;
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

0	0	0	0	0	
0	1500	1500	1500	1500	
0	1500	1500	1500	3000	
0	1500	1500	2000	3500	
第3个商品放入背包
第1个商品放入背包
1
2
3
4
5
6

其他资料

参考资料：
动态规划 (第1讲)
算法-动态规划 Dynamic Programming–从菜鸟到老鸟
 动态规划：从入门到放弃

还是没看懂，状态转移方程写不出来
在这里插入图片描述

KMP

应用场景-字符串匹配问题

字符串匹配问题：

有一个字符串 str1= ““硅硅谷尚硅谷你尚硅尚硅谷你尚硅谷你尚硅你好””，和一个子串 str2=“尚硅谷你尚硅你”

现在要判断 str1 是否含有 str2, 如果存在，就返回第一次出现的位置, 如果没有，则返回-1

暴力匹配算法

如果用暴力匹配的思路，并假设现在 str1 匹配到 i 位置，子串 str2 匹配到 j 位置，则有：

如果当前字符匹配成功（即 str1[i] == str2[j]），则 i++，j++，继续匹配下一个字符
如果失配（即 str1[i]! = str2[j]），令 i = i - (j - 1)，j = 0。相当于每次匹配失败时，i 回溯，j 被置为 0。
用暴力方法解决的话就会有大量的回溯，每次只移动一位，若是不匹配，移动到下一位接着判断，浪费了大量的时间

package com.atguigu.kmp;

/**
 * @ClassName ViolenceMatchDemo
 * @Author Jeri
 * @Date 2022-03-02 22:11
 * @Description 字符串暴力匹配
 */
public class ViolenceMatchDemo {

    public static int violenceMatch(String str1,String str2){
        char[] s1 = str1.toCharArray();
        char[] s2 = str2.toCharArray();

        int s1Len = s1.length;
        int s2Len = s2.length;

        int i = 0;//i索引指向s1
        int j = 0;//j索引指向s2

        while (i < s1Len && j < s2Len){
            if(s1[i] == s2[j]){
                i++;
                j++;
            }else{
                //回溯
                i = (i - j) + 1;
                j = 0;

            }
        }

        if(j == s2Len){
            return i-j;
        }else{
            return -1;
        }
    }

    public static void main(String[] args) {
        //测试暴力匹配算法
        String s1 = "硅硅谷 尚硅谷你尚硅 尚硅谷你尚硅谷你尚硅你好";
        String s2 = "尚硅谷你尚硅你";

        int index = violenceMatch(s1,s2);
        System.out.println("index = " + index);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

index = 15
1

KMP算法介绍

假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置

如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++，继续匹配下一个字符；
如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]。此举意味着失配时，模式串P相对于文本串S向右移动了j - next [j] 位。

next 数组各值的含义：代表当前字符之前的字符串中，有多大长度的相同前缀后缀。例如如果next [j] = k，代表j 之前的字符串中有最大长度为k 的相同前缀后缀。

对于字符串：“bread” 前缀：b ，br ，bre ，brea 后缀：read ，ead ，ad ，d

KMP的next 数组相当于告诉我们：当模式串中的某个字符跟文本串中的某个字符匹配失配时，模式串下一步应该跳到哪个位置，移动模式串，使得公共前后缀里的前缀直接移动到原来的后缀所在位置。

注意：KMP next数组求解 KMP算法学习

代码展示：

package com.atguigu.kmp;

import java.util.Arrays;

/**
 * @ClassName KMPDemo
 * @Author Jeri
 * @Date 2022-03-03 11:41
 * @Description TODO
 */
public class KMPDemo {

    public static int[] KMPNext(String dest){
        //创建 next 数组保存部分匹配值的结果
        int[] next = new int[dest.length()];
        //字符串长度为1 部分匹配值为0
        next[0] = 0;
        for(int i = 1,j = 0;i < dest.length();i++){
            while (j > 0 && dest.charAt(i) != dest.charAt(j)){
                j = next[j - 1];
            }
            if(dest.charAt(i) == dest.charAt(j)){
                j++;
            }
            next[i] = j;
        }
        return next;
    }

    public static int kmpSearch(String str,String substr,int[] next){
        //遍历
        for(int i = 0,j = 0;i < str.length();i++){

            //KMP算法处理失配  回溯 j 的位置进行重新匹配
            while (j > 0 && str.charAt(i) != substr.charAt(j)){
                j = next[j-1];
            }

            if(str.charAt(i) == substr.charAt(j)){
                j++;
            }

            if(j == substr.length()){
                return i - j + 1;
            }
        }

        return -1;
    }

    public static void main(String[] args) {

        String str = "BBC ABCDAB ABCDABCDABDE";
        String substr = "ABCDABD";

        int[] next = KMPNext(substr);

        System.out.println("子串的next数组：" + Arrays.toString(next));

        int index = kmpSearch(str,substr,next);
        System.out.println("index = " + index);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

子串的next数组：[0, 0, 0, 0, 1, 2, 0]
index = 15
1
2

KMP 注意点：

主串与子串匹配失衡时，回溯 j 的位置
子串的next数组求解

贪心算法

应用场景-集合覆盖

假设存在下面需要付费的广播台，以及广播台信号可以覆盖的地区。如何选择最少的广播台，让所有的地区都可以接收到信号

在这里插入图片描述

算法介绍

贪婪算法(贪心算法)是指在对问题进行求解时，在每一步选择中都采取最好或者最优(即最有利)的选择，从而希望能够导致结果是最好或者最优的算法

贪婪算法所得到的结果不一定是最优的结果(有时候会是最优解)，但是都是相对近似(接近)最优解的结果

思路分析

目前并没有算法可以快速计算得到准备的值，使用贪婪算法，则可以得到非常接近的解，并且效率高。选择策略上，因为需要覆盖全部地区的最小集合：

遍历所有的广播电台, 找到一个覆盖了最多未覆盖的地区的电台(此电台可能包含一些已覆盖的地区，但没有关系）
将这个电台加入到一个集合中(比如 ArrayList), 想办法把该电台覆盖的地区在下次比较时去掉
重复第 1 步直到覆盖了全部的地区

代码实现

package com.atguigu.greed;

import java.security.Key;
import java.util.*;

/**
 * @ClassName GreedDemo
 * @Author Jeri
 * @Date 2022-03-03 22:14
 * @Description 贪心算法解决集合覆盖
 */
public class GreedDemo {

    //创建广播电台 放入 map 对象
    public static HashMap<String,HashSet<String>>  broadcasts;
    // allAreas 存放所有的地区对象
    public static HashSet<String> allAreas ;


    public static void LoadData(){
        HashSet<String> set1 = new HashSet<>();
        set1.add("北京");
        set1.add("上海");
        set1.add("天津");

        HashSet<String> set2 = new HashSet<String>();
        set2.add("广州");
        set2.add("北京");
        set2.add("深圳");

        HashSet<String> set3 = new HashSet<String>();
        set3.add("成都");
        set3.add("上海");
        set3.add("杭州");

        HashSet<String> set4 = new HashSet<String>();
        set4.add("上海");
        set4.add("天津");

        HashSet<String> set5 = new HashSet<String>();
        set5.add("杭州");
        set5.add("大连");

        //将所有电台添加到 map 对象 单一添加
        broadcasts = new HashMap<>();
        broadcasts.put("K1", set1);
        broadcasts.put("K2", set2);
        broadcasts.put("K3", set3);
        broadcasts.put("K4", set4);
        broadcasts.put("K5", set5);

        //allAreas 存放所有的地区
        allAreas = new HashSet<>();
        allAreas.addAll(set1);
        allAreas.addAll(set2);
        allAreas.addAll(set3);
        allAreas.addAll(set4);
        allAreas.addAll(set5);


    }

    public static ArrayList<String> greed(){
        //定义集合 存储最后结果
        ArrayList<String> result = new ArrayList<>();
        //定义临时集合 存储临时结果
        HashSet<String> tempSet = new HashSet<>();

        // maxKey 表示与所在地区重叠最多对应的电台
        String maxKey;
        int maxCountArea;

        //遍历所有区域
        while (allAreas.size() > 0){
            maxKey = null;
            maxCountArea = 0;

            //遍历所有广播电台 找到与当前区域重叠最多对应的那个电台
            for(String key:broadcasts.keySet()){
                //临时集合清零
                tempSet.clear();
                //获取当前电台 覆盖的区域
                HashSet<String> area = broadcasts.get(key);
                tempSet.addAll(area);
                //求出 tempSet 与 allAreas 重叠的区域
                tempSet.retainAll(allAreas);

                if(tempSet.size() > maxCountArea){
                    maxCountArea = tempSet.size();
                    maxKey = key;
                }

            }

            if(maxKey != null){

                result.add(maxKey);
                allAreas.removeAll(broadcasts.get(maxKey));

                System.out.println();
                System.out.println("当前选择广播台：" + maxKey);
                System.out.println("当前选择广播台重叠个数：" + maxCountArea);
                System.out.println("未覆盖区域：" + allAreas);
            }
        }

        return result;
    }

    public static void main(String[] args) {
        //加载数据
        LoadData();

        System.out.println("广播台" + "\t覆盖地区");
        for (HashMap.Entry<String, HashSet<String>> entry : broadcasts.entrySet()) {
            System.out.println(entry.getKey() + "\t\t" + entry.getValue());
        }
        System.out.println();

        System.out.println("所有的区域如下：");
        System.out.println(allAreas);

        ArrayList<String> result = greed();
        System.out.println();
        System.out.println("选择广播：" + result);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128

广播台	覆盖地区
K1		[上海, 天津, 北京]
K2		[广州, 北京, 深圳]
K3		[成都, 上海, 杭州]
K4		[上海, 天津]
K5		[大连, 杭州]

所有的区域如下：
[成都, 上海, 广州, 天津, 大连, 杭州, 北京, 深圳]

当前选择广播台：K1
当前选择广播台重叠个数：3
未覆盖区域：[成都, 广州, 大连, 杭州, 深圳]

当前选择广播台：K2
当前选择广播台重叠个数：2
未覆盖区域：[成都, 大连, 杭州]

当前选择广播台：K3
当前选择广播台重叠个数：2
未覆盖区域：[大连]

当前选择广播台：K5
当前选择广播台重叠个数：1
未覆盖区域：[]

选择广播：[K1, K2, K3, K5]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

注意事项

贪婪算法所得到的结果不一定是最优的结果(有时候会是最优解)，但是都是相对近似(接近)最优解的结果

比如上题的算法选出的是 K1, K2, K3, K5，符合覆盖了全部的地区

但是我们发现 K2, K3,K4,K5 也可以覆盖全部地区，如果 K2 的使用成本低于 K1,那么我们上题的 K1, K2, K3, K5 虽然是满足条件，但是并不是最优的.

参考文献

尚硅谷Java数据结构与java算法

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/寸_铁/article/detail/770593

程序员常用 10 种算法_程序算法

程序员常用 10 种算法上篇

二分查找算法(非递归)

分治算法

基本介绍

基本步骤

汉诺塔

动态规划

应用场景 01背包

算法介绍

01背包思路分析

代码实现

其他资料

KMP

应用场景-字符串匹配问题

暴力匹配算法

KMP算法介绍

贪心算法

应用场景-集合覆盖

算法介绍

思路分析

代码实现

注意事项

参考文献