数据结构8---查找

一、静态查找和动态查找

（一）静态查找

静态查找:数据集合稳定，不需要添加,删除元素的查找操作。

对于静态查找来说，我们不妨可以用线性表结构组织数据，这样可以使用顺序查找算法，如果我们再对关键字进行排序，则可以使用折半查找算法或斐波那契查找算法等来提高查找的效率。

1、顺序查找

顺序查找又叫线性查找，是最基本的查找技术，它的查找过程是:从第一个（或者最后一个）记录开始，逐个进行记录的关键字和给定值进行比较，若某个记录的关键字和给定值相等，则查找成功。如果查找了所有的记录仍然找不到与给定值相等的关键字，则查找不成功。

// a 为要查找的数组，n 为要查找的数组长度，key 为要查找的关键字
int Sq_Search(int* a, int n, int key) {
	int i;
	for (i = 0; i < n; i++) {
		if (a[i] == key)
			return i;
	}
	return 0;
}

2、平均查找长度

平均查找长度:将查找算法进行的关键码的比较次数的数学期望值定义为平均查找长度。计算公式为: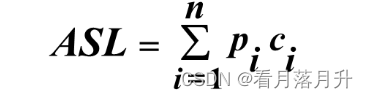

其中: n:问题规模，查找集合中的记录个数;

pi:查找第i个记录的概率;

查找第i个记录所需的关键码的比较次数。

结论:c;取决于算法;p,与算法无关,取决于具体应用。如果p ;是已知的,则平均查找长度只是问题规模的函数。

顺序查找的平均查找长度计算：

         

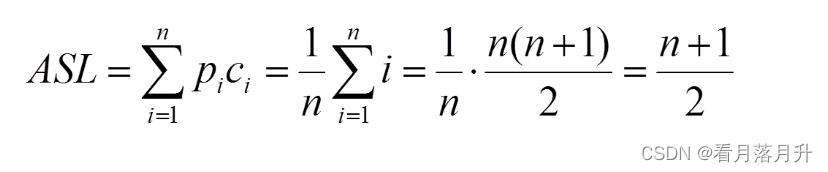
3、有序表的查找——二分查找

二分查找的基本原理如下： 1、确定要查找区间的左右端点 left 和 right；
2、计算中间位置 mid = (left + right) / 2；
3、比较中间位置 mid 的值和要查找的目标值 target：
（1）如果 mid 的值等于目标值 target，则找到了目标值；
（2）如果 mid 的值大于目标值 target，则在左半边的区间 [left, mid-1] 继续查找；
（3）如果 mid 的值小于目标值 target，则在右半边的区间 [mid+1, right] 继续查找；
4、重复上述步骤，直到找到目标元素或者区间不存在为止。

非递归代码：

#include <stdio.h> 
 
int binarySearch(int arr[], int n, int x)
{
    int left = 0; 
    int right = n - 1; 
    while (left <= right)
    { 
        int mid = left + (right - left) / 2; 
        if (arr[mid] == x)
        {
            return mid;
        }
        else if (arr[mid] < x) 
        {
            left = mid + 1;
        }
        else 
        {
            right = mid - 1;
        }
    }
    return -1; 
}
 
int main()
{
    int arr[] = { 1,2,3,4,5,6,7,8,9 }; // 有序数组
    int n = sizeof(arr) / sizeof(arr[0]); // 数组长度
    int x = 3; // 目标值
    int result = binarySearch(arr, n, x); // 调用二分查找函数
    if (result == -1) // 如果返回-1，则说明未找到目标值
    {
        printf("Element is not present in array");
    }
    else //否则，返回目标值在数组中的下标
    {
        printf("Element is present at index : %d", result);
    }
    return 0;
}

 递归代码：

#include<stdlib.h>
#include<stdio.h>
 
int binarySearch(int elem[], int low, int high, int k) {
    if (low > high)
        return -1;
    else {
        int mid = (low + high) / 2;
        if (k < elem[mid])
            return binarySearch(elem, low, mid - 1, k);
        else if (k > elem[mid])
            return binarySearch(elem, mid + 1, high, k);
        else
            return mid;
    }
 
}
 
 
int main()
{
    int arr[] = { 1,2,3,4,5,6,7,8,9 }; // 有序数组
    int n = sizeof(arr) / sizeof(arr[0]); // 数组长度
    int x = 3; // 目标值
    int result = binarySearch(arr, 0, n-1,x); // 调用二分查找函数
    if (result == -1) // 如果返回-1，则说明未找到目标值
    {
        printf("Element is not present in array");
    }
    else //否则，返回目标值在数组中的下标
    {
        printf("Element is present at index : %d", result);
    }
    return 0;
}

 （二）动态查找

动态查找:数据集合在查找的过程中需要同时添加或删除元素的查找操作。

1、二叉排序树

二叉排序树（又名二叉查找树）或者是一棵空树；或者是具有以下性质的二叉树：
1）若它的左子树不为空，则左子树上所有结点的值均小于它根节点的值
2）若它的右子树不为空，则右子树上所有结点的值均大于它根节点的值
3）它的左右子树也分别为二叉排序树

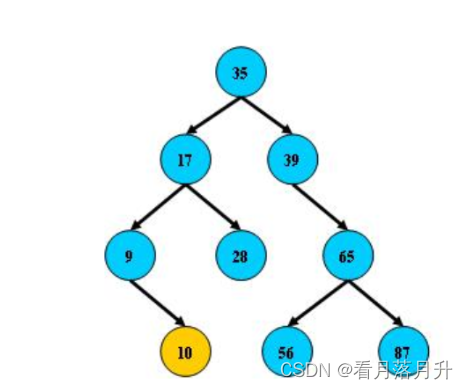
结构体定义：

#include<stdio.h>
#include<stdlib.h>
 
//二叉排序树节点存储方式
typedef int DataType;
typedef struct binarytreenode {
    DataType data;    //数据域
    struct binarytreenode* left;    //左指针 
    struct binarytreenode* right;    //右指针
}BTnode;

插入节点操作：

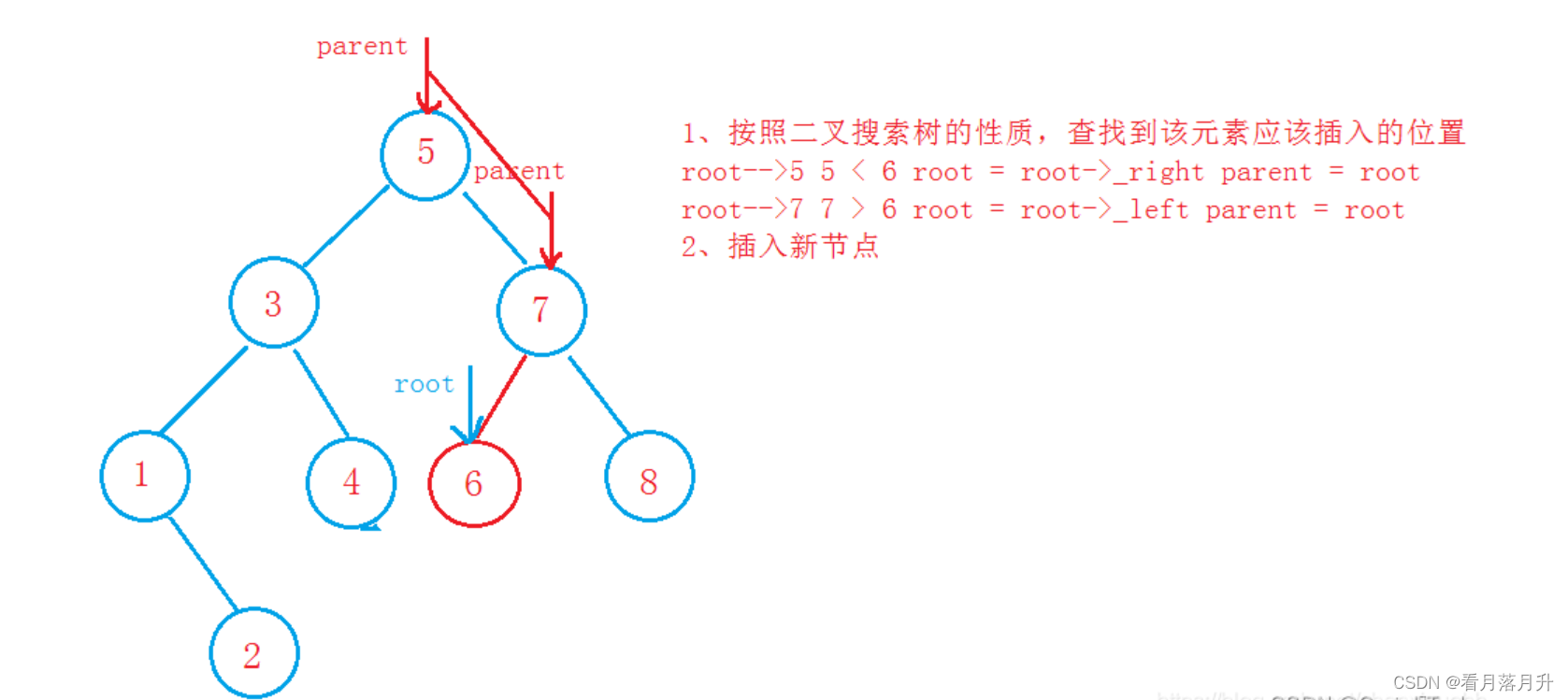
代码

//插入数据
void Insert_node(BTnode** root, DataType data) {
	if (*root == NULL) {
		*root = (BTnode*)malloc(sizeof(BTnode));
		if (!*root) {
			printf("ERROR\n");
			exit(-1);
		}
		(*root)->data = data;
		(*root)->left = NULL;
		(*root)->right = NULL;
	}
 
	else if ((*root)->data <= data)
		Insert_node(&(*root)->right, data);
	else if ((*root)->data > data)
		Insert_node(&(*root)->left, data);
}

总的代码

#include<stdio.h>
#include<stdlib.h>
 
//二叉排序树节点存储方式
typedef int DataType;
typedef struct binarytreenode {
	DataType data;	//数据域
	struct binarytreenode* left;	//左指针 
	struct binarytreenode* right;	//右指针
}BTnode;
 
 
//插入数据
void Insert_node(BTnode** root, DataType data) {
	if (*root == NULL) {
		*root = (BTnode*)malloc(sizeof(BTnode));
		if (!*root) {
			printf("ERROR\n");
			exit(-1);
		}
		(*root)->data = data;
		(*root)->left = NULL;
		(*root)->right = NULL;
	}
 
	else if ((*root)->data <= data)
		Insert_node(&(*root)->right, data);
	else if ((*root)->data > data)
		Insert_node(&(*root)->left, data);
}
 
 
//创建排序二叉树
BTnode* Create_sortBtree(DataType* arr, int size) {
	if (!arr)
		return NULL;
	else {
		BTnode* T = NULL;
		for (int i = 0; i < size; i++) {
			Insert_node(&T, arr[i]);
		}
		return T;
	}
}
 
//中序遍历排序二叉树
void mid_travel(BTnode* T)
{
	if (!T)
		return;
	mid_travel(T->left);
	printf("%d ", T->data);
	mid_travel(T->right);
}
 
//递归查找数据
BTnode* Btree_search(BTnode* root, DataType target) {
	if (!root)
		return NULL;
	if (target == root->data) {
		return root;
	}
	return target > root->data ? Btree_search(root->right, target) : Btree_search(root->left, target);
}
//非递归查找
BTnode* Btree_search_fa(BTnode* T, DataType target) {
	BTnode* p = T, * f = NULL;
	while (p) {
		if (p->data == target)
		{
			return f;
		}
		f = p;
		p = target > p->data ? p->right : p->left;
	}
	return NULL;
}
 
//获取最大值
int Btree_max(BTnode* T) {
	BTnode* cur = T;
	while (cur->right) {
		cur = cur->right;
	}
	return cur->data;
}
//获取最小值
int Btree_min(BTnode* T) {
	BTnode* cur = T;
	while (cur->left) {
		cur = cur->left;
	}
	return cur->data;
}
 
 
//删除节点
void Btree_del(BTnode* T, DataType l) {
	if (!T) {
		printf("fuck no\n");
		return;
	}
	//找到这个要删除节点的父节点
	BTnode* p = T, * f = NULL;
	while (p) {
		if (p->data == l)
		{
			break;
		}
		f = p;
		p = l > p->data ? p->right : p->left;
	}
	if (!p)
	{
		printf("没有这个节点\n");
		return;
	}
	BTnode* target = p;//此时的要删除目标节点
	BTnode* par = f; //此时要删除节点的父节点
 
	//第一种情况 此节点只有一个子树的时候
	if (!target->left && target->right != NULL)
	{
		if (target->data > par->data) {
			par->right = target->right;
		}
		else {
			par->left = target->right;
		}
		free(target);//释放空间
		target = NULL;
	}
	else if (target->left != NULL && !target->right) {
		if (target->data > par->data) {
			par->right = target->left;
		}
		else {
			par->left = target->left;
		}
		free(target);
		target = NULL;
	}
	//第二种情况，如果删除的是叶节点，直接删除即可
	else if (!target->left && !target->right) {
		if (target->data > par->data) {
			par->right = NULL;
		}
		else {
			par->left = NULL;
		}
		free(target);
		target = NULL;
	}
	//第三种情况,如果左右子树都存在的话
	//可以用右子树的最小元素
	//或者左子树的最大元素来替代被删除的节点
	//我这里就直接去用左树的最大代替这个节点
	else
	{
		BTnode* Lchild = target->left;
		BTnode* Lchild_par = NULL;//要找的替换节点的父节点
		while (Lchild->right != NULL) {
			Lchild_par = Lchild;
			Lchild = Lchild->right;
			
		}
	
		if (Lchild->left!=NULL) {
			Lchild_par->right = Lchild->left;
		}
		else
			Lchild_par->right = NULL;
		target->data = Lchild->data;
		free(Lchild);
		Lchild = NULL;
	}
	printf("Deleting successfully\n");
}
 
//销毁
void Destory_btree(BTnode* T) {
	if (!T)
		return;
	BTnode* cur = T;
	if (cur->left)
		Destory_btree(cur->left);
	if (cur->right)
		Destory_btree(cur->right);
	free(T);
}
 
int main()
{
	int a[] = { 53,17,78,9,45,65,87,23 };
	//创建二叉排序树
	BTnode* T = Create_sortBtree(a, sizeof(a) / sizeof(int));
	mid_travel(T);//遍历输出
	puts("");
	//删除最大最小值
	printf("max:%d  min:%d\n", Btree_max(T), Btree_min(T));
	//查找
	BTnode* find = Btree_search(T, 23);
	printf("查找结果%d\n", find->data);
 
	//删除节点
	Btree_del(T, 45);
	mid_travel(T);
	puts("");
	//销毁操作
	Destory_btree(T);
}
//输出结果：
//9 17 23 45 53 65 78 87
//max:87  min : 9
//查找结果23
//Deleting successfully
//9 17 23 53 65 78 87
 

2、平衡二叉树

平衡二叉树的目的是为了减少二叉查找树层次，提高查找速度。
平衡二叉树或为空树,或为如下性质的二叉排序树:
（1）左右子树深度之差的绝对值不超过1;
（2）左右子树仍然为平衡二叉树.

平衡因子BF(Balance Factor)

若将二叉树上结点的平衡因子BF(Balance Factor)定义为该结点的左子树的深度减去它的右子树的深度，则平衡二叉树上左右结点的平衡因子只能是-1、0和1.只要二叉树上有一个结点的BF的绝对值大于1，这个二叉树就是不平衡的。

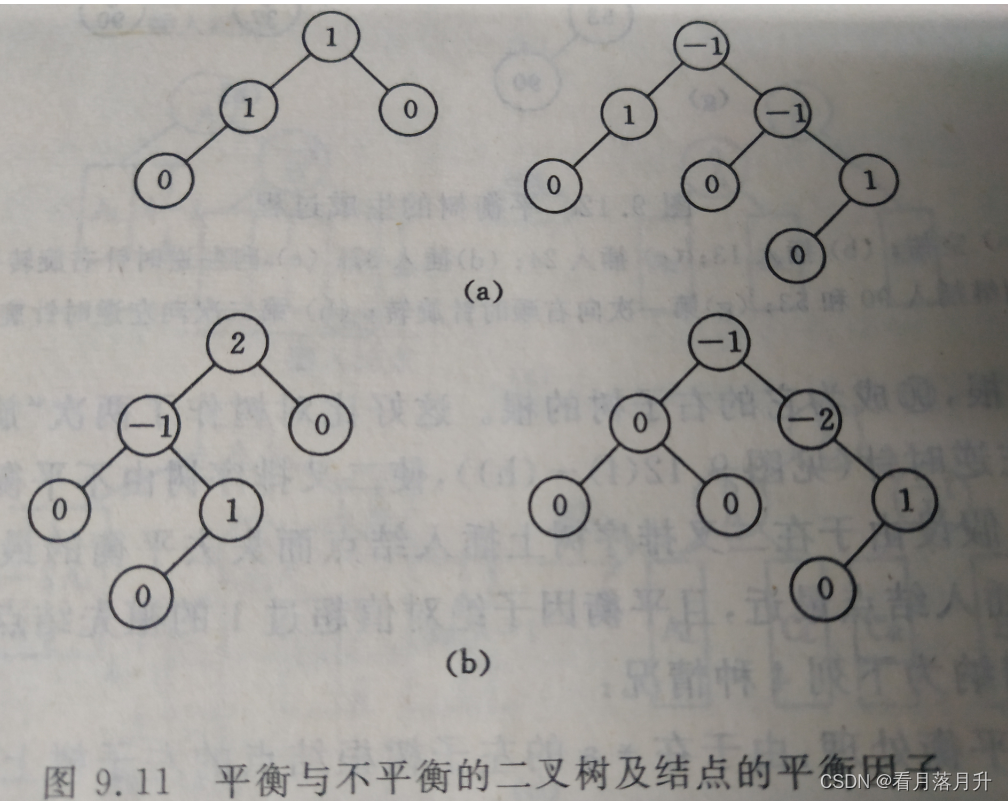
如何进行自平衡

可分为四种：

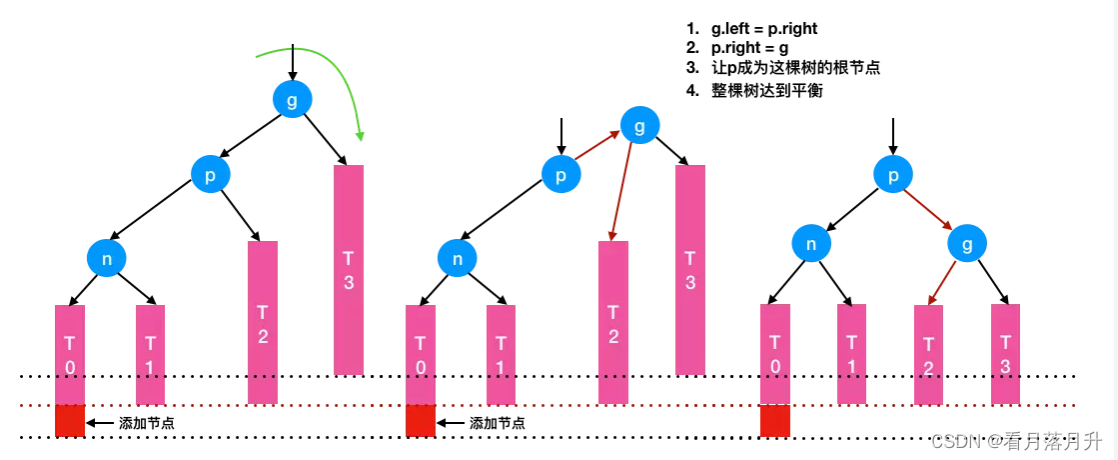
1、LL（左左）：由于在* a的左子树根节点的左子树上插入结点，* a的BF由1增至2，致使以* a为根节点的子树失去平衡。需要一次向右的顺时针旋转操作
示例：在子树T0上添加新节点后，根节点g的左右子树失衡，g->T0 比 g->T3 深度多了2。需对g节点执行一次右旋转，具体步骤为：

g.left = p.right;  //g的左孩子指向p的右孩子
p.right = g;  //g变成p的右孩子
root = p;  //p作为新的根

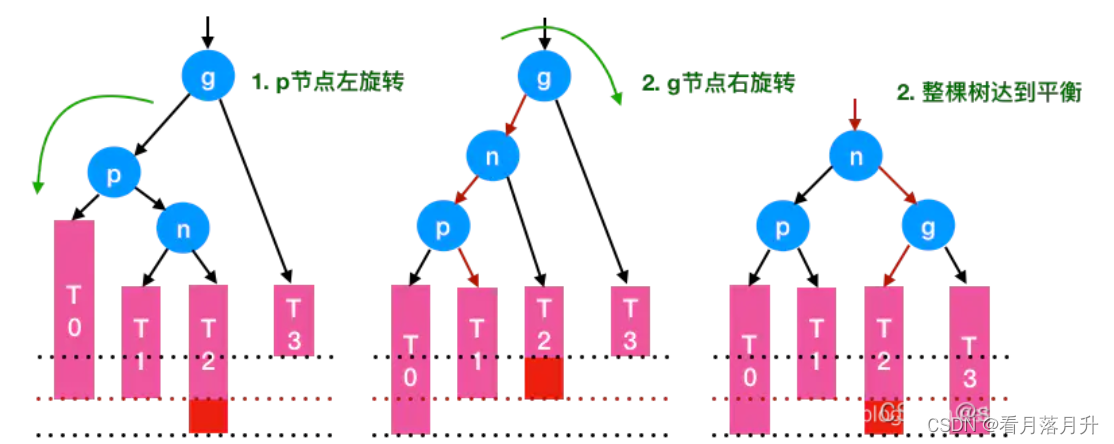
2、LR（左右）：由于在* a的左子树根节点的右子树上插入结点，* a的BF由1增至2，致使以* a为根节点的子树失去平衡。需要两次旋转（先左旋后右旋）操作
示例：在子树T2上添加新节点后，根节点g的左右子树失衡，g->T2 比 g->T3 深度多了2。这时先对p节点执行一次左旋转（虽然以p为根的树平衡并未打破，但这是必要的准备工作），经过一次左旋后，g的左孩子的左子树“过重”失衡了，可以归于“左左”的情形。（假设新节点插入位置是子树T1，左旋后仍是“左左”的情况）再对g节点执行一次右旋转即可重新平衡：具体步骤为：2、

//左旋
p.right = n.left;  //p的左孩子指向n的右孩子
n.left = p;  //p变成n的左孩子
root = n;  //n作为子树新的根
//右旋
g.left = p.right;  //g的左孩子指向p的右孩子
p.right = g;  //g变成p的右孩子
root = p;  //p作为新的根

3、RR（右右）:左左的镜像问题。只需对g执行一次左旋（逆时针旋转）
4、RL（右左）:左右的镜像问题。先右旋后左旋。

举个例子：

#include <stdio.h>
#include <stdlib.h>
#define MAXINT 10000
#define MAXSIZE 10
typedef struct BBTnode{
    int data;//这里为了方便，直接用int,没有用结构体．
    int balance;//平衡因子
    struct BBTnode* lchild;
    struct BBTnode* rchild;
    struct BBTnode* parent;
}BBTnode,*BBTree;
BBTree MinBalance;//最小失衡结点地址
int k = 0;
int i = 0;
BBTree SearchBBT(BBTree T, int m, char* arr)//计算从某点出发，到指定数字的路径
{
    if(!T || T->data == m)
    {
        return T;
    }
    else if(m < T->data)
    {
        arr[k++] = 'L';
        return SearchBBT(T->lchild, m, arr);
    }
    else
    {
        arr[k++] = 'R';
        return SearchBBT(T->rchild, m, arr);
    }
 
}
 
int CountNodes(BBTree T)//计算树中的结点数，比较失衡结点树的大小，选择较小的树（当不止一个失衡点时）
{
    if(!T)
    {
        return 0;
    }
    return CountNodes(T->lchild) + CountNodes(T->rchild) + 1;
}
 
int DepthBBT(BBTree T)//计算平衡二叉树的深度
{
    int m, n;
    if(!T)
    {
        return 0;
    }
    else
    {
        m = DepthBBT(T->lchild) + 1;//左边的深度
        n = DepthBBT(T->rchild) + 1;//右边的深度
    }
    if(m > n)return m;//取较大值
    else return n;
}
 
 
void OrderBBT(BBTree* T, BBTree Unbalance[MAXSIZE])//中序遍历二叉排序树,更新各结点平衡因子，把所有失衡点存储起来
{
    if(*T == NULL)return;
    else
    {
        OrderBBT(&(*T)->lchild,Unbalance);
        (*T)->balance = abs(DepthBBT((*T)->lchild) - DepthBBT((*T)->rchild));//计算该结点平衡因子，左边深度－右边深度再取绝对值
        if((*T)->balance>1)
        {
            Unbalance[i++] = *T;
        }
        OrderBBT(&(*T)->rchild,Unbalance);
    }
}
 
void AddBBT(BBTree* T, int m, BBTree parent)//二叉排序树的递归添加元素
{
    if(!(*T))
    {
        *T = malloc(sizeof(BBTnode));
        (*T)->data = m;
        (*T)->lchild = NULL;
        (*T)->rchild = NULL;
        (*T)->balance = 0;
        (*T)->parent = parent;
    }
    else if(m < (*T)->data)
    {
        AddBBT(&(*T)->lchild, m, *T);
    }
    else
    {
        AddBBT(&(*T)->rchild, m, *T);
 
    }
}
 
 
void creatBBT(BBTree* T)//创建平衡二叉排序树，实际上就是给一个空树添加元素
{
    int input = 1;
    BBTree A,B,C;//定义图示中表示的三个顶点
    while(input)
    {
        printf("请依次输入数字序列，输入完毕以0结束:>");
        scanf("%d",&input);
        if(input == 0)break;
        AddBBT(T, input,*T);
        MinBalance = 0;//重置最小平衡因子为空
        int temp = MAXINT;
        int j;
        BBTree Unbalance[MAXSIZE] = {0};//定义一个失衡结点数组，用来存放当前树中存在的失衡结点
        i = 0;//重置数组Unbalance的下标为0开始
        OrderBBT(T,Unbalance);//更新平衡因子，得到平衡因子数组Unbalance
        for(j = 0; j < MAXSIZE; j++)//从数组Unbalance找出最小失衡因子，并返回该地址到MinBalance
        {
            if(!Unbalance[j])break;
            if(CountNodes(Unbalance[j]) < temp)
            {
                temp = CountNodes(Unbalance[j]);
                MinBalance = Unbalance[j];
            }
        }
        char ChoiceType[MAXSIZE] = {0};//选择调整类型的数组（ＬＬ，ＲＲ．ＬＲ，ＲＬ）
        k = 0;//重置SearchBBT里的k变量
        SearchBBT(MinBalance, input, ChoiceType);//得到从失衡点出发到添加结点间的路径
        if(ChoiceType[0] == 'L' && ChoiceType[1] == 'L')//ＬＬ型调整
        {
            A = MinBalance;
            B = MinBalance->lchild;
            C = MinBalance->lchild->lchild;
            if(A->parent)//如果这个失衡点不是根结点
            {
                if(A->data < A->parent->data)A->parent->lchild = B;
                else A->parent->rchild = B;
            }
            else *T = B;
 
            A->lchild = B->rchild;
            if(B->rchild)B->rchild->parent = A;
            B->rchild = A;
            B->parent = A->parent;
            A->parent = B;
 
        }
        else if(ChoiceType[0] == 'R' && ChoiceType[1] == 'R')//ＲＲ型调整
        {
            A = MinBalance;
            B = MinBalance->rchild;
            C = MinBalance->rchild->rchild;
            if(A->parent)//如果这个失衡点不是根结点
            {
                if(A->data < A->parent->data)A->parent->lchild = A->rchild;
                else A->parent->rchild = A->rchild;
            }
            else *T = B;//如果是根结点，那么根结点变成调整后的根结点
            A->rchild = B->lchild;
            if(B->lchild)B->lchild->parent = A;
            B->lchild = A;
            B->parent = A->parent;
            A->parent = B;
 
 
 
        }
        else if(ChoiceType[0] == 'L' && ChoiceType[1] == 'R')//ＬＲ型调整
        {
            A = MinBalance;
            B = MinBalance->lchild;
            C = MinBalance->lchild->rchild;
            if(A->parent)//如果这个失衡点不是根结点
            {
                if(A->data < A->parent->data)A->parent->lchild = C;
                else A->parent->rchild = C;
            }
            else *T = C;
            B->rchild = C->lchild;
            if(C->lchild)C->lchild->parent =B;
            A->lchild = C->rchild;
            if(C->rchild)C->rchild->parent = A;
            C->rchild = A;
            C->lchild = B;
            C->parent = A->parent;
            A->parent = C;
            B->parent = C;
 
        }
        else if(ChoiceType[0] == 'R' && ChoiceType[1] == 'L')//ＲＬ型调整
        {
            A = MinBalance;
            B = MinBalance->rchild;
            C = MinBalance->rchild->lchild;
            if(A->parent)//如果这个失衡点不是根结点
            {
                if(A->data < A->parent->data)A->parent->lchild = C;
                else A->parent->rchild = C;
            }
            else *T = C;
            A->rchild = C->lchild;
            if(C->lchild)C->lchild->parent = A;
            B->lchild = C->rchild;
            if(C->rchild)C->rchild->parent = B;
            C->lchild = A;
            C->rchild = B;
            C->parent = A->parent;
            A->parent = C;
            B->parent = C;
        }
    }
    BBTree arr[MAXSIZE] = {0};//这个只为为了下面这个OrderBBT函数能运行，没有别的意义
    OrderBBT(T,arr);
}
void printBBT(BBTree T)//中序输出二叉排序树，得到的是一个递增数列
{
    if(T == NULL)return;
    else
    {
        printBBT(T->lchild);
        printf("%d号结点平衡因子为%d\n",T->data,T->balance);
        printBBT(T->rchild);
    }
}
 
int main()
{
    BBTree T = NULL;//定义二叉排序树Ｔ
    creatBBT(&T);//创建二叉排序树
    printBBT(T);//输出创建好的二叉排序树
    return 0;
}

二、哈希查找

1、原理

哈希查找是一种快速查找算法，该算法不需要对关键字进行比较，而是以关键字为自变量，以该关键字在存储空间中的地址为因变量，建立某种函数关系，称为哈希函数，这样在查找某一关键字的时候，就可以通过哈希函数直接得到其地址，有效的提高了查找效率。
选取哈希函数及基本原则主要有：计算函数所需时间、关键字的长度、哈希表长度（哈希地址范围）、关键字分布情况、记录的查找频率等。
哈希函数的构造有多种，常见的有“直接定址法”、“数字分析法”、“平方取中法”、“折叠法”、“除留余数法”、“随机数法”等。
哈希函数构造的一个基本原则就是尽量避免冲突，也就是尽量避免因变量地址的冲突。一旦发生冲突，就需要重新定址。常见的处理地址冲突的方法有：“开放定址法”、“再哈希法”、“链地址法”、“建立公共溢出区”等。

2、创建哈希查找及哈希插值表示例

假设有数据{ 10, 8, 14, 15, 20, 31 }，创建哈希表以进行哈希查找。

1.创建哈希表

长度取 n+1
以除留余数法构造哈希函数，以线性探测法作为处理冲突的方法，取哈希表长度为7，建立哈希表过程如下：
H(10) = 10 % 7 = 3
H(8) = 8 % 7 = 1
H(14) = 14 % 7 = 0
H(15) = 15 % 7 = 1 此时冲突，重新定址：H(15) = (H(15)+1) % 7 = 2
H(20) = 20 % 7 = 6
H(31) = 31 % 7 = 3 此时冲突，重新定址：H(31) = (H(31)+1) % 7 = 4
哈希表如下：

2.哈希查找

当查找某一元素的时候，首先通过哈希函数计算其哈希地址，然后比较该地址的值是否等于目标值，如果相等则查找结束，否则利用处理冲突的方法确定新的地址，再进行比较。如果哈希地址为空，则查找失败。
利用哈希函数计算元素15的地址是1，此时表里的元素不等于15，因此使用线性探测法更新哈希地址，得到新地址是2，此时查找成功。

结构体

typedef struct HashTable
{
	int key;      //关键字 
	int EmptyFlag;//占用（冲突）标志，0表示没被占用，1表示被占用 
}HashTable;

 创建哈希表

//tbl：哈希表
//data：已知的数组
//m：数组的长度
//p：哈希表的长度 
void CreateHashTable( HashTable *tbl, int *data, int m, int p )
{
	int i, addr, k;
	for( i=0; i<p; i++ ) //把哈希表被占用标志置为0 
	{
		tbl[i].EmptyFlag = 0;
	}
	for( i=0; i<m; i++ )
	{
		addr = data[i] % p;//计算哈希地址 
		k = 0;//记录冲突次数 
		while( k++ < p )
		{
			if( tbl[addr].EmptyFlag == 0 )
			{
				tbl[addr].EmptyFlag = 1;//表示该位置已经被占用 
				tbl[addr].key   = data[i];
				break;
			}
			else
			{
				addr =  ( addr + 1 ) % p; //处理冲突 
			}
		}	
	}
}

哈希查找

int SearchHashTable( HashTable *tbl, int key, int p )
{
	int addr, k, loc;//loc表示查找位置下标，如果为0则表示查找失败 
	addr = key % P;//计算Hash地址 
	loc = -1; 
	k = 0;//记录冲突次数 
	while( k++ < p )
	{
		if( tbl[addr].key == key )
		{
			loc = addr;
			break;
		}
		else
		{
			addr =  ( addr + 1 ) % p; //处理冲突 
		}	
	}
	return loc;
}

代码如下

#include"stdio.h"
#define M 6
#define P (M+1)
typedef struct HashTable
{
	int key;      //关键字 
	int EmptyFlag;//占用（冲突）标志，0表示没被占用，1表示被占用 
}HashTable;
 
void CreateHashTable( HashTable *tbl, int *data, int m, int p );
int SearchHashTable( HashTable *tbl, int key, int p );
 
int main()
{
	HashTable HashTbl[P];
	int data[M] = { 10, 8, 14, 15, 20, 31 };
	int i, loc;
	printf( "初始数据：\n" );
	for( i=0; i<M; i++ )
	{
		printf( "data[%d] = %5d\n", i, data[i] );
	}
	printf( "\n" );
	CreateHashTable( HashTbl, data, M, P );
	printf( "哈希表：  \n" );
	for( i=0; i<M; i++ )
	{
		printf( "tbl[%d] = %5d\n", i, HashTbl[i].key );
	}
	printf( "\n" );
	for( i=0; i<M; i++ )
	{
		loc = SearchHashTable( HashTbl, data[i], P );
		printf( "%5d 's loc = %5d\n", data[i], loc );
	}
	
	return 0;
}
void CreateHashTable( HashTable *tbl, int *data, int m, int p )
{
	int i, addr, k;
	for( i=0; i<p; i++ ) //把哈希表被占用标志置为0 
	{
		tbl[i].EmptyFlag = 0;
	}
	for( i=0; i<m; i++ )
	{
		addr = data[i] % p;//计算哈希地址 
		k = 0;//记录冲突次数 
		while( k++ < p )
		{
			if( tbl[addr].EmptyFlag == 0 )
			{
				tbl[addr].EmptyFlag = 1;//表示该位置已经被占用 
				tbl[addr].key   = data[i];
				break;
			}
			else
			{
				addr =  ( addr + 1 ) % p; //处理冲突 
			}
		}	
	}
}
 
int SearchHashTable( HashTable *tbl, int key, int p )
{
	int addr, k, loc;//loc表示查找位置下标，如果为0则表示查找失败 
	addr = key % P;//计算Hash地址 
	loc = -1; 
	k = 0;//记录冲突次数 
	while( k++ < p )
	{
		if( tbl[addr].key == key )
		{
			loc = addr;
			break;
		}
		else
		{
			addr =  ( addr + 1 ) % p; //处理冲突 
		}	
	}
	return loc;
}

后面还有查找的方法，会更新的