热门标签
热门文章
- 1【Caddy】Caddy实践1——此网站无法提供安全连接_安装caddy出错
- 2Git Cherry-Pick命令详解:轻松选取与移植提交_cherrypick 多个提交
- 3手把手教NLP小白如何用PyTorch构建和训练一个简单的情感分类神经网络_训练一种词向量,利用pytorch,搭建情感分析的深度模型运行截图
- 4Nginx 配置特定IP访问_nginx只允许指定ip访问
- 5NLP案例——命名实体识别(Named Entity Recongition)_nlp命名实体识别
- 6uibotrga初级/中级认证选择题答案_uibot初级认证选择题答案
- 7自定义view的简单实现(一)_简单实现自定义view
- 8cadence从原理图到pcb_cadence原理图转pcb
- 9LabelMe和x-anyLabeling标注工具的合二为一版_anylabelme
- 10brew常见命令 自用 实践笔记_慎用 brew upgrade
当前位置: article > 正文
DFS(深度优先搜索)和BFS(宽度优先搜索)_宽度搜索代码
作者:天景科技苑 | 2024-06-19 18:11:41
赞
踩
宽度搜索代码

目录
DFS(深度优先搜索)
深度优先搜索(Depth First Search,DFS)是十分常见的图搜索方法之一。深度优先搜索会沿着一条路径一直搜索下去,在无法搜索时,回退到刚刚访问过的节点。深搜优先搜索的本质上就是持续搜索,遍历了所有可能的情况。DFS搜索的流程是一个树的形式,每次一条路走到低。
全排列的DFS解法

- public class DFS {
- public static void main(String[] args) {
- DFS(0, "", 3);
- }
-
- public static void DFS(int depth, String ans, int n) {
- if (depth == n) {//深度等于n时就输出
- System.out.print(ans + " ");
- return;
- }
- for (int i = 1; i <= n; i++) {
- DFS(depth + 1, ans + i, n);
- }
- }
- }
如果不对其进行剪枝操作,就会将所有的子叶全部输出

所以在需要要求全排列的情况下我们就需要进行剪枝,也就是对递归循环进行判断
- public class DFS {
- public static void main(String[] args) {
- DFS(0, "", 3);
- }
-
- public static void DFS(int depth, String ans, int n) {
- if (depth == n) {//深度等于n时就输出
- System.out.print(ans + " ");
- return;
- }
- for (int i = 1; i <= n; i++) {
- if (! ans.contains("" + i)) {
- //目前已经生成的ans串用过的不能再用(剪枝)
- DFS(depth + 1, ans + i, n);
- }
- //public boolean contains(CharSequence s)
- // 当且仅当此字符串包含指定的 char 值序列时,返回 true。
- }
- }
- }

这样得到的结果就是全排列后的结果了
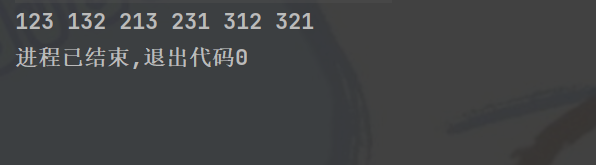
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/天景科技苑/article/detail/737304
推荐阅读
相关标签


