喵喵爱编程

这个屌丝很懒，什么也没留下！

热门标签

ANN 向量搜索：基于 SQL 的 LSH 和随机投影_sql 局部敏感哈希

作者：喵喵爱编程 | 2024-08-11 23:24:07

踩

sql 局部敏感哈希

本文字数：17920；估计阅读时间：45 分钟

审校：庄晓东（魏庄）

本文在公众号【ClickHouseInc】首发

介绍

今年早些时候，我们探索了 ClickHouse 中的向量搜索功能。虽然这主要集中在蛮力线性技术上，其中搜索向量与 ClickHouse 中的每个向量进行比较，同时满足其他过滤条件，但我们也涉及了最近添加的新近似最近邻技术。这些技术目前在 ClickHouse 中处于实验阶段，支持 Annoy 和 HNSW。

虽然传统的博客文章可能会探讨这些算法、它们的实现以及它们在 ClickHouse 中的使用，但我们的首席技术官和创始人 Alexey Milovidov 认为，大多数数据问题都可以通过 SQL 来解决。几个月前，他在西班牙的一次聚会上提出了一种使用随机投影和 SQL 构建向量索引的替代方法。在本文中，我们探索 Alexey 的方法，并测试和评估其有效性。

快速回顾

向量嵌入是概念的数字表示，由一系列浮点数（可能是数千个）组成，表示高维空间中的位置。这些嵌入通常由机器学习模型生成，例如亚马逊的 Titan，并且可以为任何媒介（如文本和图像）创建。在这个高维空间中，彼此接近的向量表示类似的概念。对于三维空间（大多数人可以理解的最高维度数量），可以进行可视化：

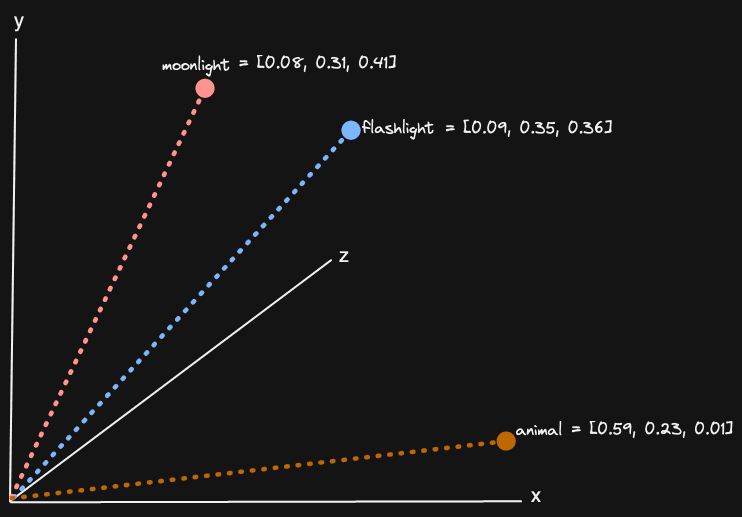
我们在以前的帖子中详细探讨了这个概念，包括为什么这是有用的。在向量搜索中，问题归结为查找与搜索向量相似的大型集合中的那些向量嵌入，这些嵌入通常通过使用相同模型的查询生成。因此，我们实际上是在寻找与我们的搜索查询相似的向量，从而间接找到了与我们搜索查询相似的内容。这个查询可以是任何媒介。

同样，在这个上下文中，这等同于两个向量之间的距离或角度。数学（通常是余弦相似度或欧氏距离）用于计算这些统计数据，并且可以扩展到 N 个维度。这个问题的最简单解决方案是一个简单的线性扫描：

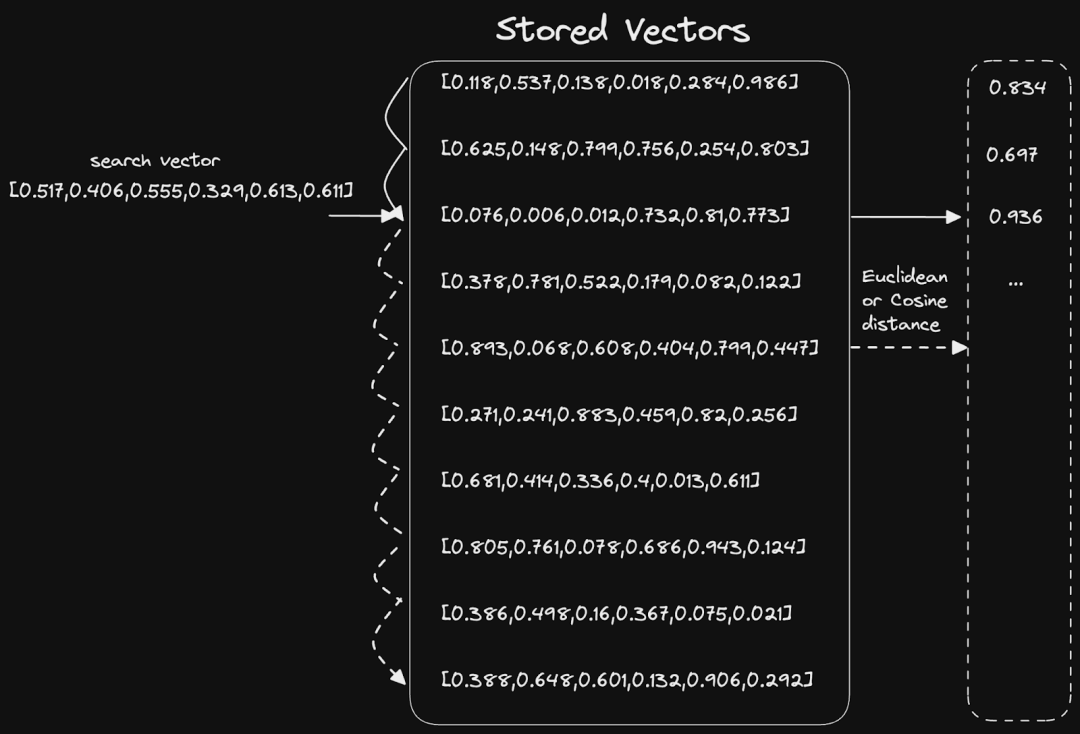
向量索引

虽然线性扫描可能非常快速且足够，特别是如果高度并行化，例如在 ClickHouse 中，但也有可能使用一些数据结构来降低 O(n) 复杂度。这些数据结构或向量索引被近似算法所利用，这些算法通常需要在高召回率（检索到的相关记录数与总相关记录数的比率 - 假设我们有一个最小相似度）和低延迟之间进行权衡。

这些近似算法通常称为近似最近邻（ANN）。这个命名暗示了试图近似地找到最近的向量的一般问题。

我们的线性扫描方法具有 100% 的召回率，但在数十亿行时实现可接受的延迟可能会具有挑战性。在理论上，这些算法通过牺牲一些召回率来以更低的计算成本提供更低的延迟响应。实际上，它们返回一个近似的结果集，这可能是足够的，只要“最佳结果”的足够百分比仍然存在。

通常，这些算法的质量被呈现为召回率 - 延迟曲线或召回率 - QPS（每秒查询数）曲线：

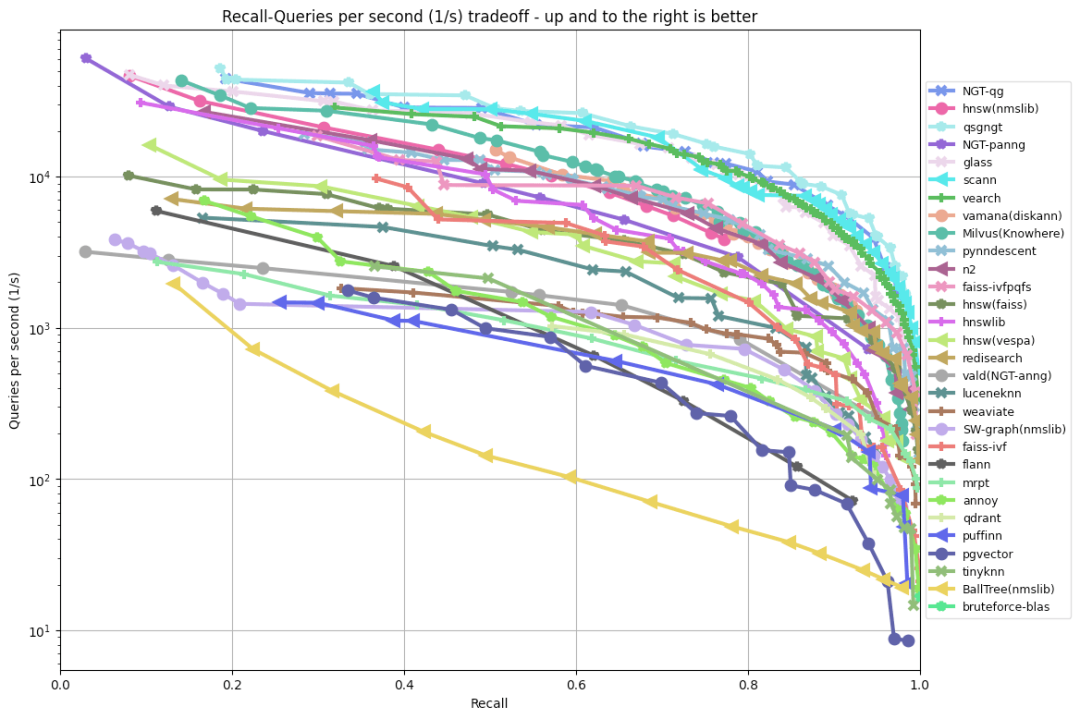
查看 ANN benchmarks （https://ann-benchmarks.com/index.html）

虽然这给了我们一个性能指标，但它通常代表了一个理想的设置。它未能衡量出现在生产环境中的其他重要因素。例如，这些算法也具有不同程度的支持，允许更新向量以及它们是否可以轻松持久化到磁盘或必须完全在内存中运行。我们的简单线性扫描不受这些限制的影响。

虽然我们认识到像 HNSW 这样的算法的价值（因此我们已经添加到了 ClickHouse 中），也许我们可以回归到问题的基本原理，并加速向量的搜索，同时保留更新向量集合的能力，并且不受内存的限制。

在这种精神下，并且因为 Alexey 喜欢在 SQL 中执行所有操作，他提出了一种基于局部敏感哈希（LSH）和随机投影的简单向量索引。

使用局部敏感哈希（LSH）和随机投影

以下方法的核心目标是将我们的向量编码为降低维度但保留它们的分布和彼此的局部性的表示。有了这种较低维度的表示，我们应该能够更有效地计算它们的相似性（关于内存和 CPU）。尽管我们预期这会降低我们相似性计算的准确性和召回率（由于我们通过降低维度而导致的信息丢失，它变得成为一个估计），但我们预计质量应该足够好，同时仍然从更快的搜索时间中受益。正如我们将展示的，我们也可以将这种方法与准确的距离计算相结合。

这种方法依赖于局部敏感哈希或 LSH。LSH 是一种哈希函数，它将数据向量转换为较低维度表示的哈希，使得在原始域中接近的那些向量在其结果哈希中也接近。这实际上是传统哈希函数的反面，后者的目标是最小化碰撞并确保此相似性不被保留。在我们的情况下，我们的 LSH 是基于随机投影的，结果哈希是一个位序列。在原始空间中接近的向量应该具有相似的 1 和 0 的序列。

这里的实现相对简单，带我们回到了一些高中数学。假设我们的向量在高维空间中大致均匀分布（如果它们不是，则参见利弊）。

目标是使用 N 个随机超平面（N 由用户配置）来划分我们的高维空间。一旦定义了这些平面，我们记录向量位于每个平面的哪一侧，使用简单的 1 或 0。这为每个向量提供了一个位集表示，其中的每个位位置描述了向量位于随机平面的哪一侧。因此，我们的位序列的长度将与我们选择的超平面数相同。

让我们看一个简化的例子，假设我们的向量只有两个维度。在这种情况下，我们的超平面是通过一个通过原点 0,0 的向量定义的线。

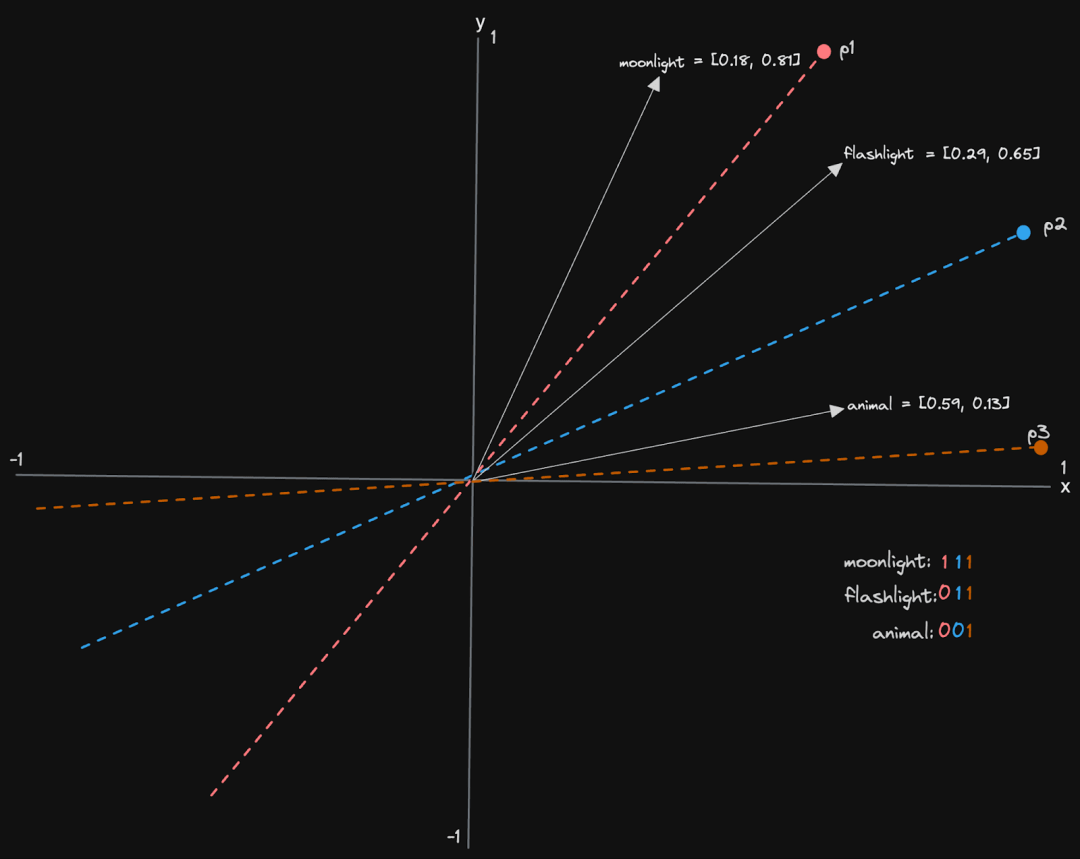
我们有三个平面 p1、p2 和 p3，每个向量都有一个 3 位序列。对于每个平面，我们记录向量是否在线的上方或下方，对于前者记录 1，对于后者记录 0。“moonlight” 的向量位于所有线的上方，因此具有位序列 111。相反，“flashlight” 位于 p1 的下方，但位于 p2 和 p3 的上方，结果是 011。上面的假设是我们的向量在单位空间内，即 -1 到 1（并非总是如此），并且我们有一个在线的上方和下方的概念（我们上面的示例可能直观，但不适用于空间中的所有向量）。

因此，这里有两个结果问题：我们如何计算一个向量位于线的上方还是下方？我们如何选择我们的线？

要选择我们的线，我们有几种选择。如果我们的向量是归一化的（-1 到 1），我们可以从归一化分布中对空间进行采样，选择一个随机点。我们希望这些向量理想上在空间的表面上均匀分布（实际上是单位球体）。要实现这一点，需要使用 Norm。这一点可以被视为一个随机投影，它将通过原点，并通过它的正交/法向量定义我们的线/平面高维空间。这个法向量将用于与我们的线/平面对其他向量进行比较。

但是，Alexey 的示例假设这些向量没有被归一化。因此，他使用的解决方案旨在将向量移动到接近归一化空间。虽然这不会创造出对归一化空间的完美均匀性，但它确实提高了随机性。这通过在空间中取两个随机向量 v1 和 v2 并计算它们之间的差异来实现，将其标记为法向量（(v1 - v2)），这个法向量定义了超平面。还计算了这些向量的偏移或中点（(v1 + v2) / 2），并用于将向量投影到此范围以与法向量进行比较，方法是减去它的值。

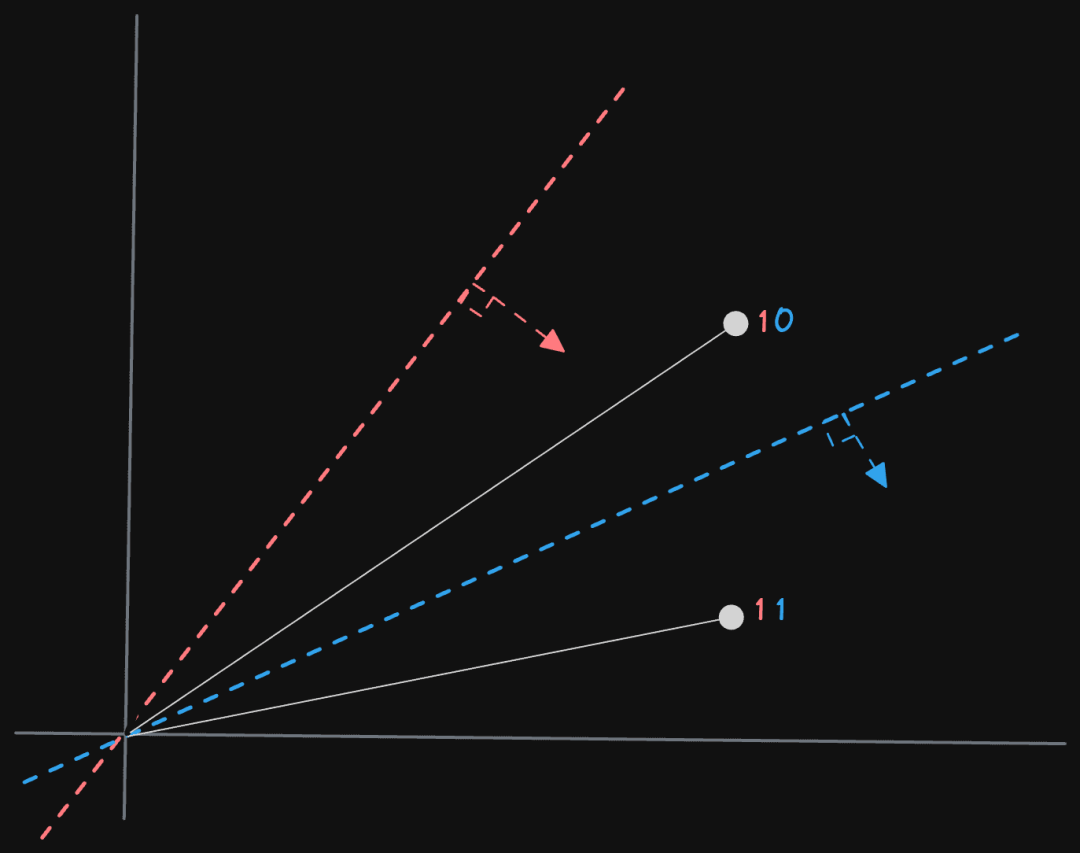
我们可以使用上述定义的法向量的简单点积来计算一个向量是在线的上方还是下方。点积是两个向量的相应分量的乘积的总和，这个标量值表示输入向量的相似性或对齐。如果向量指向同一方向，值将为正数（1 表示同一方向）。负值意味着它们处于相反的方向（-1 完全相反），而值为 0 表示它们是正交的。因此，我们可以使用正值来表示在线的“上方”，0 或更小值表示“下方”。

对于上面的非归一化情况，我们计算法向量和(v - 偏移)的点积。在前进过程中，我们将使用后面的方法，因为它更健壮，但稍后会返回到简单的情况，以显示潜在的更简单的语法和稍微更好的性能。

显然，此时，我们必须想象更高的维度。然而，原则仍然是相同的。我们选择空间中的两个随机点，计算它们之间的向量，并记录中点。我们使用此平面信息来计算点是否与线相交。

上述计算实际上起到了我们的 LSH 函数的作用，并将每个向量投影到了一个较低维度的空间中，从而为每个向量表示为位序列的哈希。这个序列可以计算表中每个向量嵌入以及为搜索查询生成的嵌入。我们可以通过比较位序列来估计两个向量的接近程度。在理论上，重叠的位序列越多，共享超平面的边就越多。一个简单的汉明距离，它测量不同的位数，就足够了。

ANN 的纯 SQL 解决方案

定义平面

以上在 Python 或任何编程语言中实现起来相对简单。但是，ClickHouse 对于这个任务来说是理想的。我们不仅可以仅使用几行 SQL 定义上述内容，而且我们还将利用 ClickHouse 的所有优势，包括根据元数据进行过滤、聚合以及不受内存限制。在插入新向量时，还需要在插入时计算行的嵌入序列。

对于我们的测试数据集，我们将使用来自 Glove 的测试集，其中包含从 840B CommonCrawl 标记中训练的 2.1m 个向量。此集合中的每个向量都有 300 个维度，表示一个单词。

对于我们的测试，我们将使用具有 16 个核心的 ClickHouse Cloud 实例。

我们使用以下模式来定义我们的目标表。如前面的帖子中所讨论的，ClickHouse 中的向量只是 32 位浮点数的数组。


 
CREATE TABLE glove
(
  `word` String,
  `vector` Array(Float32)
)
ENGINE = MergeTree
ORDER BY word

加载此数据集，我们可以使用 ClickHouse local 从客户端获取字符串和数组函数来提取单词和向量。


 
clickhouse local --query "SELECT trim(splitByChar(' ', line)[1]) as word, arraySlice(splitByChar(' ', line),2) as vector FROM file('glove.840B.300d.zip :: glove.840B.300d.txt','LineAsString') FORMAT Native" | clickhouse client --host <host> --secure --password '<password>' --query "INSERT INTO glove FORMAT Native"

加载完成后，我们需要定义我们的平面。我们将这些存储在一个表中以便快速查找：


 
CREATE TABLE planes (      
  normal Array(Float32),  
  offset Array(Float32)
) 
ENGINE = MergeTree 
ORDER BY ()

在这里，偏移和法线将是两个随机向量的中点和差，如前所述。我们将使用简单的 INSERT INTO SELECT 来填充这个表。请注意，此时我们需要定义要使用的平面数量。

对于下面的示例，我们选择使用 128 个平面来开始。这将导致每个向量的 128 位比特序列，可以使用 UInt128 表示。要创建 128 个平面，我们需要 256 个随机向量（每个平面 2 个）。我们使用 intDiv(rowNumberInAllBlocks(), 2) 表达式来对这个随机集进行分组，并使用 min 和 max 函数来确保为每个随机点选择不同的向量。


 
SELECT min(vector) AS v1, max(vector) AS v2
FROM
(
  SELECT vector
  FROM glove
  ORDER BY rand() ASC
  LIMIT 256
)
GROUP BY intDiv(rowNumberInAllBlocks(), 2)

上面的操作给我们带来了 128 行，每行两个随机向量 v1 和 v2。我们需要执行向量差以计算我们的 '法线' 列。简单的减法就可以做到这一点。中点，在上述表中称为偏移，可以使用 (v1 + v2)/2 来计算。


 
INSERT INTO planes SELECT v1 - v2 AS normal, (v1 + v2) / 2 AS offset
FROM
(
  SELECT
        min(vector) AS v1,
        max(vector) AS v2
  FROM
  (
        SELECT vector
        FROM glove
        ORDER BY rand() ASC
        LIMIT 256
  )
  GROUP BY intDiv(rowNumberInAllBlocks(), 2)
)
 
0 rows in set. Elapsed: 0.933 sec. Processed 2.20 million rows, 2.65 GB (2.35 million rows/s., 2.84 GB/s.)
Peak memory usage: 4.11 MiB.

在 Alexey 的原始演讲中，他使用了表达式 `arrayMap((x, y) -> (x - y), v1, v2)` 和 `arrayMap((x, y) -> ((x + y) / 2), v1, v2)` 来计算向量差和中点。随后，ClickHouse 添加了向量算术功能，允许使用简单的 `+`、`-` 和 `/` 来构建这些操作。这带来了显著更快的效果！

构建比特哈希

创建了我们的平面之后，我们可以继续为我们现有的每个向量创建比特哈希。为此，我们将使用早期的模式创建一个新表 glove_lsh，其中包含一个 UInt128 类型的 bits 字段（因为我们有 128 个平面）。这将有效地成为我们的索引。请注意，我们按列对表进行排序以加速后续的过滤操作。有关如何加速过滤操作的更多详细信息，请参见利弊。


 
CREATE TABLE glove_lsh
(
  `word` String,
  `vector` Array(Float32),
  `bits` UInt128
)
ENGINE = MergeTree
ORDER BY (bits, word)
SETTINGS index_granularity = 128

我们还将表的 index_granularity 降低到 128。这被确认为一个重要的优化，因为通常，我们会返回少量的结果，并且相关的向量应该分布在相同的颗粒集中，即具有相似的比特哈希。修改此设置会减小我们的颗粒大小，因此在较少的行上执行次要扫描。正如后面所示，我们可能还希望使用距离函数对向量进行重新评分（以获得更准确的相关性评分）。该函数的计算密集度更高，减少执行此函数的行数将有助于提高响应时间。

要填充我们的表，我们需要计算每个向量的位掩码。请注意，在这里我们使用 16 核的实例加载了 200 万个向量需要 100 秒。


INSERT INTO glove_lsh
WITH
   128 AS num_bits,
   (
       SELECT
           groupArray(normal) AS normals,
           groupArray(offset) AS offsets
       FROM
       (
           SELECT *
           FROM planes
           LIMIT num_bits
       )
   ) AS partition,
   partition.1 AS normals,
   partition.2 AS offsets
SELECT
   word,
   vector,
   arraySum((normal, offset, bit) -> bitShiftLeft(toUInt128(dotProduct(vector - offset, normal) > 0), bit), normals, offsets, range(num_bits)) AS bits
FROM glove
SETTINGS max_block_size = 1000
 
0 rows in set. Elapsed: 100.082 sec. Processed 2.20 million rows, 2.69 GB (21.94 thousand rows/s., 26.88 MB/s.)

此查询的第一部分使用具有 groupArray 函数的 CTE，将我们的平面定位到一个包含两列的单行中，每列包含 128 个向量。这两列包含我们之前讨论的所有中点和差向量。在这个结构中，我们能够将这些传递到负责计算每个向量的比特哈希的表达式中：


 
arraySum((normal, offset, bit) -> bitShiftLeft(toUInt128(dotProduct(vector - offset, normal) > 0), bit), normals, offsets, range(num_bits)) AS bits

对于每一行执行此表达式。arraySum 函数对包含 128（num_bits）个元素的数组的结果进行求和。这通过一个 lambda 函数来执行，对于每个数组元素 i，计算（向量 - 偏移）⋅法线，其中偏移和法线是来自第 i 个平面的向量。这是我们前面描述的点积计算，确定向量位于平面的哪一侧。这个计算的结果与 0 进行比较，得到一个布尔值，我们通过 toUInt128 函数将其转换为 UInt128。将这个值向左移动 n 个位置，得到一个值，其中只有第 i 位设置为 1（如果点积为真）和 0（否则）。这个第 i 位有效地表示这个向量与第 i 个平面的关系。我们将这些整数求和以得到一个十进制 UInt128，其二进制表示形式是我们的比特哈希。

在上面的插入中，我们将 max_block_size 减小到 1000。这是因为 arraySum 函数的状态具有较高的内存开销，原因是平面在内存中。具有许多行的大块因此可能会很昂贵。通过减小块大小，我们减少了一次处理的行数和状态。


 
SELECT *
FROM glove_lsh
LIMIT 1
FORMAT Vertical
 
Row 1:
──────
word:   CountyFire
vector: [-0.3471,-0.75666,...,-0.91871]
bits:   6428829369849783588275113772152029372 <- how bit hash in binary

创建索引后，我们使用以下查询评估其大小：


 
SELECT name, formatReadableSize(sum(data_compressed_bytes)) AS compressed_size,
  formatReadableSize(sum(data_uncompressed_bytes)) AS uncompressed_size,
  round(sum(data_uncompressed_bytes) / sum(data_compressed_bytes), 2) AS ratio
FROM system.columns
WHERE table LIKE 'glove_lsh'
GROUP BY name
ORDER BY name DESC
 
┌─name───┬─compressed_size─┬─uncompressed_size─┬─ratio─┐
│ word   │ 8.37 MiB         │ 12.21 MiB          │  1.46 │
│ vector │ 1.48 GiB         │ 1.60 GiB           │  1.08 │
│ bits   │ 13.67 MiB        │ 21.75 MiB          │  1.59 │
└────────┴─────────────────┴───────────────────┴───────┘

我们的 bits 列比我们的向量小了100倍以上。现在的问题是，这种对空间的压缩表示是否更快速地进行查询...

查询

在使用我们的索引之前，让我们测试一个简单的蛮力搜索，使用余弦距离（作为 glove 推荐的方法）来提供绝对质量的基准和我们可以认为是权威结果的结果。在下面的示例中，我们搜索与单词 "dog" 相似的单词：


 
WITH
   'dog' AS search_term,
   (
       SELECT vector
       FROM glove
       WHERE word = search_term
       LIMIT 1
   ) AS target_vector
SELECT
   word,
   cosineDistance(vector, target_vector) AS score
FROM glove
WHERE lower(word) != lower(search_term)
ORDER BY score ASC
LIMIT 5
 
 
┌─word────┬──────score─┐
│ dogs    │ 0.11640698 │
│ puppy   │ 0.14147866 │
│ pet     │ 0.19425482 │
│ cat     │ 0.19831467 │
│ puppies │ 0.24826884 │
└─────────┴────────────┘
 
10 rows in set. Elapsed: 0.515 sec. Processed 2.21 million rows, 2.70 GB (2.87 million rows/s., 3.51 GB/s.)
Peak memory usage: 386.24 MiB.

为了简单起见，我们使用我们的 glove 索引查找结果。在真实的搜索场景中，我们的单词不太可能在索引中，并且需要生成向量嵌入，例如使用 embed UDF 函数。

对于相同的查询，我们需要使用我们的索引为我们的术语构造上面的位哈希。对于我们的目标向量的位与每行中的位之间的汉明距离计算，我们使用 bitHammingDistance 函数。

对于 UInt128 使用 bitHammingDistance 函数需要 ClickHouse 23.11。在早期版本上的用户应该使用 bitCount(bitXor(bits, target)) 来计算 UInt128 的汉明距离。


 
WITH 'dog' AS search_term,
   (
       SELECT vector
       FROM glove
       WHERE word = search_term
       LIMIT 1
   ) AS target_vector,
   128 AS num_bits,
   (
       SELECT
           groupArray(normal) AS normals,
           groupArray(offset) AS offsets
       FROM
       (
           SELECT *
           FROM planes
           LIMIT num_bits
       )
   ) AS partition,
   partition.1 AS normals,
   partition.2 AS offsets,
   (
       SELECT arraySum((normal, offset, bit) -> bitShiftLeft(toUInt128(dotProduct(target_vector - offset, normal) > 0), bit), normals, offsets, range(num_bits))
   ) AS target
SELECT word
FROM glove_lsh WHERE word != search_term
ORDER BY bitHammingDistance(bits, target) ASC
LIMIT 5
 
┌─word─────┐
│ animal   │
│ pup      │
│ pet      │
│ kennel   │
│ neutered │
└──────────
 
5 rows in set. Elapsed: 0.086 sec. Processed 2.21 million rows, 81.42 MB (25.75 million rows/s., 947.99 MB/s.)
Peak memory usage: 60.40 MiB.

快得多！结果与 cosineDistance 函数返回的精确结果不同，但在很大程度上似乎是有意义的。

由此距离估计返回的质量可能会随着向量空间本身以及随机位置如何将其分区而变化。还存在一些质量估计不足的情况。如果质量不佳，或者我们需要更精确的排序，该索引还可以用于在匹配结果重新评分之前对结果集进行预过滤，并可能限制为满足阈值的结果。这是一种常见的技术，在许多传统搜索系统中，其中使用术语查找，并且使用矢量（或其他相关性）函数重新对结果进行评分。


 
WITH
   'dog' AS search_term,
   (
       SELECT vector
       FROM glove
       WHERE word = search_term
       LIMIT 1
   ) AS target_vector,
   128 AS num_bits,
   (
       SELECT
           groupArray(normal) AS normals,
           groupArray(offset) AS offsets
       FROM
       (
           SELECT *
           FROM planes
           LIMIT num_bits
       )
   ) AS partition,
   partition.1 AS normals,
   partition.2 AS offsets,
   (
       SELECT arraySum((normal, offset, bit) -> bitShiftLeft(toUInt128(dotProduct(target_vector - offset, normal) > 0), bit), normals, offsets, range(num_bits))
   ) AS target
SELECT
   word,
   bitHammingDistance(bits, target) AS approx_distance,
   cosineDistance(vector, target_vector) AS score
FROM glove_lsh
PREWHERE approx_distance <= 5
WHERE word != search_term
ORDER BY score ASC
LIMIT 5
 
┌─word───┬─approx_distance─┬──────score─┐
│ dogs   │             4  │ 0.11640698 │
│ pet   │             3  │ 0.19425482 │
│ cat   │             4  │ 0.19831467 │
│ pup   │             2  │ 0.27188122 │
│ kennel │             4  │  0.3259402 │
└────────┴─────────────────┴────────────┘
 
5 rows in set. Elapsed: 0.079 sec. Processed 2.21 million rows, 47.97 MB (28.12 million rows/s., 609.96 MB/s.)
Peak memory usage: 32.96 MiB.

因此，我们在性能上实现了10倍的提速，并保持了质量！敏锐的读者可能已经注意到了根据值为5进行过滤 - 实际上，这是不同的位数，最大范围为128。我们如何选择这个值呢？

反复试验。这个值应该在不同的搜索词中是稳健的，但会取决于您的空间中向量的分布。如果值过高，会在距离评分之前过滤掉不够的行，从而提供最小的性能优势。如果值太低，则会过滤掉所需的结果。显示值分布的查询在这里可能会有所帮助。这个分布是正态分布（更具体地说是二项式分布）：


 
WITH
   'dog' AS search_term,
   (
       SELECT vector
       FROM glove
       WHERE word = search_term
       LIMIT 1
   ) AS target_vector,
   128 AS num_bits,
   (
       SELECT
           groupArray(normal) AS normals,
           groupArray(offset) AS offsets
       FROM
       (
           SELECT *
           FROM planes
           LIMIT num_bits
       )
   ) AS partition,
   partition.1 AS normals,
   partition.2 AS offsets,
   (
       SELECT arraySum((normal, offset, bit) -> bitShiftLeft(toUInt128(dotProduct(target_vector - offset, normal) > 0), bit), normals, offsets, range(num_bits))
   ) AS target
SELECT
    bitCount(bitXor(bits, target)) AS approx_distance,
    bar(c,0,200000,100) as scale,
    count() c
FROM glove_lsh
GROUP BY approx_distance ORDER BY approx_distance ASC
 
┌─approx_distance─┬──────c─┬─scale─────────────────────────────────────────────────────────────────────────┐
│             0 │     1 │                                                                                │
│             2 │     2 │                                                                                │
│             3 │     2 │                                                                                │
│             4 │   10 │                                                                                │
│             5 │   37 │                                                                                │
│             6 │     106 │                                                                                │
│             7 │     338 │ ▏                                                                              │
│             8 │     783 │ ▍                                                                              │
│             9 │   1787 │ ▉                                                                              │
│               10 │   3293 │ █▋                                                                             │
│               11 │   5735 │ ██▊                                                                            │
│               12 │   8871 │ ████▍                                                                          │
│               13 │  12715 │ ██████▎                                                                        │
│               14 │  17165 │ ████████▌                                                                      │
│               15 │  22321 │ ███████████▏                                                                   │
│               16 │  27204 │ █████████████▌                                                                 │
│               17 │  32779 │ ████████████████▍                                                              │
│               18 │  38093 │ ███████████████████                                                            │
│               19 │  44784 │ ██████████████████████▍                                                        │
│               20 │  51791 │ █████████████████████████▉                                                     │
│               21 │  60088 │ ██████████████████████████████                                                 │
│               22 │  69455 │ ██████████████████████████████████▋                                            │
│               23 │  80346 │ ████████████████████████████████████████▏                                      │
│               24 │  92958 │ ██████████████████████████████████████████████▍                                │
│               25 │ 105935 │ ████████████████████████████████████████████████████▉                          │
│               26 │ 119212 │ ███████████████████████████████████████████████████████████▌                   │
│               27 │ 132482 │ ██████████████████████████████████████████████████████████████████▏            │
│               28 │ 143351 │ ███████████████████████████████████████████████████████████████████████▋       │
│               29 │ 150107 │ ███████████████████████████████████████████████████████████████████████████   │
│               30 │ 153180 │ ████████████████████████████████████████████████████████████████████████████▌ │
│               31 │ 148909 │ ██████████████████████████████████████████████████████████████████████████▍   │
│               32 │ 140213 │ ██████████████████████████████████████████████████████████████████████         │
│               33 │ 125600 │ ██████████████████████████████████████████████████████████████▊                │
│               34 │ 106896 │ █████████████████████████████████████████████████████▍                         │
│               35 │  87052 │ ███████████████████████████████████████████▌                                   │
│               36 │  66938 │ █████████████████████████████████▍                                             │
│               37 │  49383 │ ████████████████████████▋                                                      │
│               38 │  35527 │ █████████████████▊                                                             │
│               39 │  23526 │ ███████████▊                                                                   │
│               40 │  15387 │ ███████▋                                                                       │
│               41 │   9405 │ ████▋                                                                          │
│               42 │   5448 │ ██▋                                                                            │
│               43 │   3147 │ █▌                                                                             │
│               44 │   1712 │ ▊                                                                              │
│               45 │     925 │ ▍                                                                              │
│               46 │     497 │ ▏                                                                              │
│               47 │     245 │                                                                                │
│               48 │     126 │                                                                                │
│               49 │    66  │                                                                                │
│               50 │    46  │                                                                                │
│               51 │    16  │                                                                                │
│               52 │    6   │                                                                                │
│               53 │    5   │                                                                                │
│               54 │    3   │                                                                                │
│               55 │    6   │                                                                                │
│               56 │    1   │                                                                                │
│               60 │    1   │                                                                               │
└─────────────---─┴─-──────┴───────────────────────────────────────────────────────────────────────────────┘
 
57 rows in set. Elapsed: 0.070 sec. Processed 2.21 million rows, 44.11 MB (31.63 million rows/s., 630.87 MB/s.)

正态分布在这里显而易见，大多数单词的距离都在30位左右。在这里，我们可以看到，即使是5的距离实际上也将我们过滤的结果限制在52个之内（1+2+2+10+37）。

这个距离限制在其他查询中有多稳健？下面，我们展示了各种搜索词和方法的结果：（1）如果按余弦距离对蛮力搜索进行排序，（2）按汉明距离排序，（3）按5的距离进行过滤，然后按余弦距离重新排序（4）按10的距离进行过滤，然后按余弦距离重新排序。对于这些方法的每一种，我们提供响应时间。

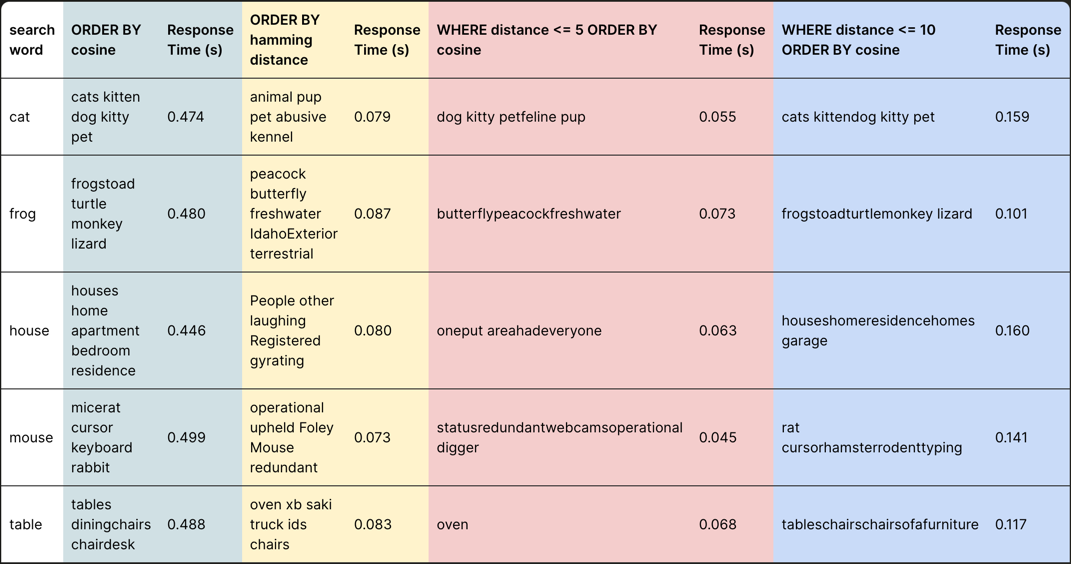
这里有几点观察：

按汉明距离排序比简单的蛮力余弦距离搜索快约6倍。然而，结果质量显著下降，不太可能稳健，我们稍后会解释原因。
将距离过滤到5并按余弦距离重新排序可提高结果质量，优于按汉明距离排序。性能也更好，响应时间比蛮力搜索快10倍。然而，结果质量似乎并不在所有搜索词中稳健，促使我们将最小距离增加到10。
将距离过滤到10并按余弦距离重新排序始终提供质量一致的结果。这种方法比标准余弦距离提供了4倍的加速。

更简单的平面

我们先前使用中点创建的平面相对复杂。如前所述，如果我们的向量是归一化的（如 glove 的情况），那么平面的创建可以简单地生成空间中代表其法向量的随机点。这些点需要在值为 -1 到 1 之间归一化，并且从正态分布中选取，即我们实际上希望均匀地从单位球体中采样点。从数学上讲，这要求我们使用向量的范数，ClickHouse 中提供了 L2Norm 函数。以下的 INSERT INTO 在一个单位球体上生成了128个点/平面，每个平面有300个维度，使用 ClickHouse 中的 randNormal 和 L2Norm 函数。这里使用了一些数组函数的复杂性 - 我们将这留给用户在限制后的利益中分解的练习。


 
INSERT INTO planes_simple SELECT projection / L2Norm(projection) AS projection
FROM
(
    SELECT arrayJoin(arraySplit((x, y) -> y, groupArray(e), arrayMap(x -> ((x % 300) = 0), range(128 * 300)))) AS projection
    FROM
    (
        SELECT CAST(randNormal(0, 1), 'Float32') AS e
        FROM numbers(128 * 300)
    )
)

在这种情况下，我们的平面只包含一个单一点。这简化了填充我们的表 glove_lsh_simple 的需要的查询。这种简化显著提高了插入时间 - 现在只有43秒（从100秒降到了43秒）。


 
INSERT INTO glove_lsh_simple
WITH
    128 AS num_bits,
    (
        SELECT groupArray(projection) AS projections
        FROM
        (
            SELECT *
            FROM planes_simple
            LIMIT num_bits
        )
    ) AS projections
SELECT
    word,
    vector,
    arraySum((projection, bit) -> bitShiftLeft(toUInt128(dotProduct(vector, projection) > 0), bit), projections, range(num_bits)) AS bits
FROM glove
SETTINGS max_block_size = 1000
 
0 rows in set. Elapsed: 43.425 sec. Processed 2.20 million rows, 2.69 GB (50.57 thousand rows/s., 61.95 MB/s.)

查询也更加简单，并且产生了可比较的结果：


 
WITH
    'dog' AS search_term,
    (
        SELECT vector
        FROM glove
        WHERE word = search_term
        LIMIT 1
    ) AS target_vector,
    128 AS num_bits,
    (
        SELECT groupArray(projection) AS projections
        FROM
        (
            SELECT *
            FROM planes_simple
            LIMIT num_bits
        )
    ) AS projections,
    (
        SELECT arraySum((projection, bit) -> bitShiftLeft(toUInt128(dotProduct(target_vector, projection) > 0), bit), projections, range(num_bits))
    ) AS target
SELECT word
FROM glove_lsh_simple
WHERE word != search_term
ORDER BY bitCount(bitXor(bits, target)) ASC
LIMIT 5
 
┌─word────┐
│ dogs    │
│ puppy   │
│ pet     │
│ doggy   │
│ puppies │
└─────────┘
 
5 rows in set. Elapsed: 0.066 sec. Processed 2.21 million rows, 81.26 MB (33.63 million rows/s., 1.24 GB/s.)
Peak memory usage: 53.71 MiB.

请注意，由于查询复杂性的降低，这里也获得了一些性能提升。

利弊

与 HNSW 等更复杂的 ANN 算法相比，这种方法具有许多优点。我们已经证明了当与窗口重新评分配合使用时，我们保留了相关性准确度，并且获得了相当大的加速 - 大约是4倍。上面的结果还显示了我们的查询具有非常低的内存开销 - 大约为50MiB。虽然这可以归因于 ClickHouse 不将所有位集存储在内存中，但索引表示也非常高效，每个向量只有128位。这种方法也不需要将索引保存在内存中，而是在磁盘上具有非常紧凑的表示，如下所示：


 
SELECT
    table,
    name,
    formatReadableSize(sum(data_compressed_bytes)) AS compressed_size,
    formatReadableSize(sum(data_uncompressed_bytes)) AS uncompressed_size
FROM system.columns
WHERE table = 'glove_lsh'
GROUP BY table, name
 
┌─table─────┬─name───┬─compressed_size─┬─uncompressed_size─┐
│ glove_lsh │ word   │ 8.37 MiB        │ 12.21 MiB         │
│ glove_lsh │ vector │ 1.48 GiB        │ 1.60 GiB          │
│ glove_lsh │ bits   │ 13.67 MiB       │ 21.75 MiB         │
└───────────┴────────┴─────────────────┴───────────────────┘
 
5 rows in set. Elapsed: 0.024 sec.

从上面可以看出，我们的 bits 列（实际上是我们的索引）在磁盘上压缩后占用了大约13MiB 的空间，而向量存储则需要1.5GiB。此外，添加额外的行也很简单且计算成本低廉 - 我们在插入时计算我们的 bits 列。最后，这种方法也适用于 ClickHouse 的并行执行模型，同时也容易分发。这可以通过向节点添加更多核心（即垂直扩展）或者将数据分片到多个节点来实现。另外，在 ClickHouse Cloud 中，数据只存储在对象存储中的一个副本，并且计算与存储分离，用户可以动态地扩展其节点。这些方法中的任何一种都可以将工作并行化，以加速查询或支持更高的 QPS 速率。

最后，可能有趣的是，这种方法如何适应 ClickHouse 特定的列式磁盘结构。敏锐的读者会注意到我们按 bits 列本身对表进行排序，即 ORDER BY（bits，word）。当按照距离 N 进行过滤并重新评分顶部结果时，我们的查询可以利用这种排序来加速查询，并避免完全线性扫描。我们的距离条件是在 PREWHERE 条件中提供的，这实际上意味着位列首先（并行）扫描以识别匹配的 granules。鉴于这一列的大小（约13MiB），在 ClickHouse 的高度矢量化查询管道中可以非常快速地完成此操作。向量列（大小显着大约为1.5GiB）仅在与我们的 PREWHERE 距离子句匹配的 granules 中加载和扫描。这两步过滤将要加载的数据最小化，并有助于我们的性能。

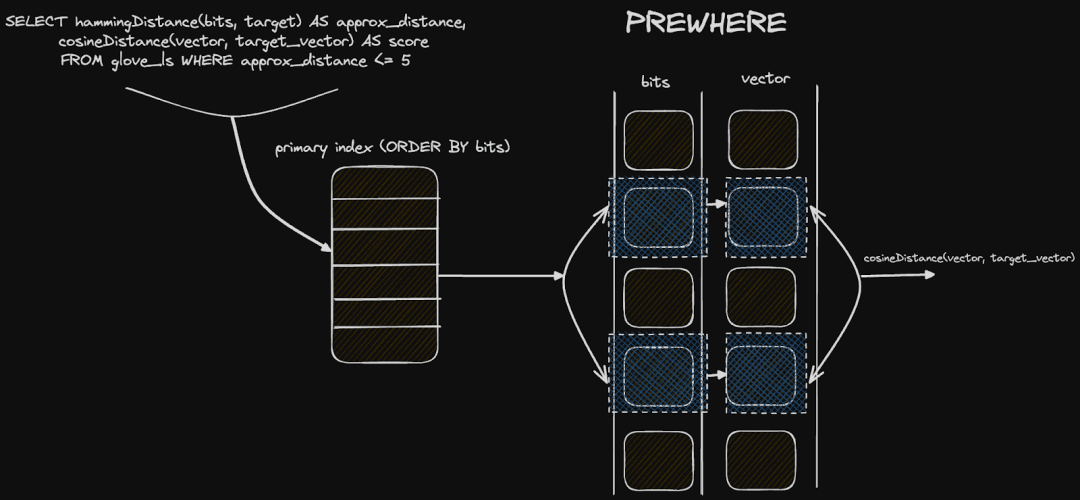
虽然上述优点清晰明了，但也有一些限制。虽然我们没有严格评估召回率，但上述方法不太可能像 HNSW 等基于图的方法一样有效。所有 ANN 算法通常都会在它们的参数化程度和用于划分和表示高维空间的数据结构大小之间做出妥协。基于图的算法高度参数化，并计算空间的粒度表示。

最重要的是，这些方法不可避免地更好地代表了“邻居”的概念。我们对空间的相当粗糙的划分假设不了解空间，并将其划分为随机生成的平面（尽管我们的中点方法在某种程度上利用了空间的一些信息，但相当粗糙）。如果平面划分这些集群，那么两个相邻向量的邻近性实际上可能会在编码中丢失。例如，请考虑下面的图表：

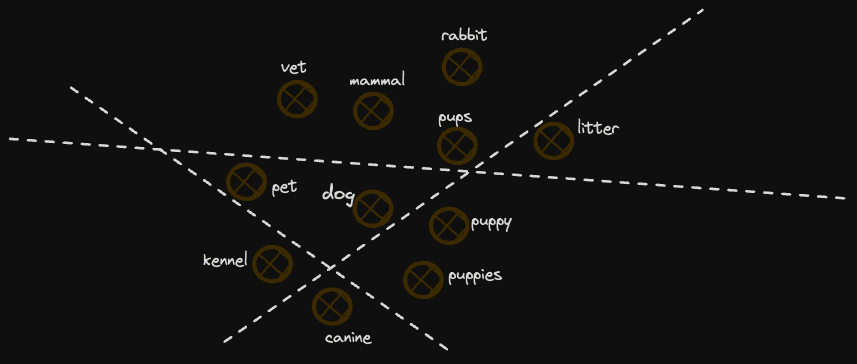
在这个例子中，我们失去了一些类似于 "dog" 的概念，因为它们位于分隔平面的两侧。随着平面数量的增加，这个问题会变得不那么严重，例如，进一步分隔这两个点的 127 个平面是不太可能的。然而，它们很可能会以一种不完美的方式划分空间，这导致了不完美的相关性。

此外，我们的距离测量相当粗糙，并且不能在不同的搜索中进行比较。特定的距离度量根据空间的位置有不同的 “接近” 概念，或者两个向量是否是 “邻居”。例如，在空间稀疏的地区，距离为 4 可能代表空间中的一个接近邻居。相反，在具有许多向量的高密度区域中，它可能是无意义的。

这里可能存在的一个类比是人们的邻居概念相对于人口密度的相对性 - 在纽约，邻居可能是对面的公寓里的人。在怀俄明州的偏远地区，可能是数十英里远。HNSW 等基于图的算法通过使用更多的参数，并实际上更详细地映射空间并更好地划分点来解决这个问题，从而提供了更优秀的最近邻度量。然而，它们在更新和在磁盘上高效地持久化方面更加昂贵。

这些因素使得我们用汉明距离计算的距离度量粗糙且仅仅是一个估计。我们使用精确余弦距离的重新评分方法可以很好地解决这个问题，同时保留了性能优势。

调优

最后，我们将简要讨论我们实际上需要多少个超平面，以及我们的位哈希应该有多大。这将导致一篇更长的博客文章，但总之，它取决于向量的数量和维度。一般来说，更多的位数 = 更好的搜索质量（和召回率），因为可以更好地参数化和划分空间，以及在我们的 LSH 值中更少的碰撞，但查询性能会减慢。

对于 glove，我们的 LSH 中有 128 位，给我们实际上是 2*128 = 3.4^1038 个哈希桶。对于 200 万个向量，这应该导致碰撞的概率非常低。哈希可能可以减少到 32 位（通过 UInt32 表示），以获得最小的碰撞。然而，我们对 glove 的简要测试表明，尽管大多数桶从未被填满 - 每个桶的向量数可以通过对位列进行简单的聚合和计数来确定 - 128 位的值提供了最佳的结果质量。虽然我们平均每个桶少于一个向量，并且没有碰撞，但将分辨率增加到超过避免碰撞所需的数量可以提高桶的精度和空间的划分。

具有更高维向量的用户可能希望尝试使用更多的位，例如 UInt256，通过更多的平面有效地划分向量。然而，需要注意的是，这会导致更多的计算开销，因为需要比较更多的位。总之，位数/平面数通常是依赖于数据集的，并且需要一些测试（特别是与距离阈值和重新评分相结合时），尽管 128 似乎是一个很好的起点。

结论

在本文中，我们探讨了 ClickHouse 用户如何使用仅 SQL 创建矢量索引以加速最近邻搜索。更具体地说，通过在高维空间中创建随机超平面并计算位序列，我们可以使用汉明距离计算来估计向量之间的距离。这种方法可以将向量搜索的速度提高10倍或精确匹配提高4倍。我们已经提出了这种方法的利弊。让我们知道您是否发现这个方法有用，并尝试在您自己的数据集上使用这个方法！

征稿启示

面向社区长期正文，文章内容包括但不限于关于 ClickHouse 的技术研究、项目实践和创新做法等。建议行文风格干货输出&图文并茂。质量合格的文章将会发布在本公众号，优秀者也有机会推荐到 ClickHouse 官网。请将文章稿件的 WORD 版本发邮件至：Tracy.Wang@clickhouse.com

联系我们

手机号：13910395701

邮箱：Tracy.Wang@clickhouse.com

满足您所有的在线分析列式数据库管理需求

本文内容由网友自发贡献，转载请注明出处：https://www.wpsshop.cn/w/喵喵爱编程/article/detail/966648