数据结构基础（四）树和二叉树_[问题描述]树和二叉树是最常用的非线性结构(树型结构),其中以二叉树最为常见

前言

树型结构是一类特别重要的非线性结构，其中以树和二叉树最为常用。

定义

• 树：
  树是n个结点的有限集。在任何一个非空树中，（1）有且仅有一个特定的称为根的结点；（2）当n>1时，其余节点可分为m个互不相交的有限集，每一个集合又是一颗树，并且称为根的子树
  
• 二叉树：
  特点为每个结点至多只有两棵子树，并且，二叉树的子树有左右之分，其次序不能任意颠倒。
  

常用术语

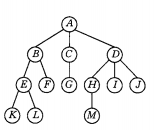
节点的度：结点拥有的子树个数称为结点的度。例如第一个图，根结点A的度为3，结点B的度为2，结点C的度为1，结点F的度为0
叶子：度为0的结点称为叶子或终端节点
树的深度：树中结点的最大层次，第一个图中树的深度为4

二叉树

分类

满二叉树：一棵深度为k且有2^k-1个结点的二叉树称为满二叉树。

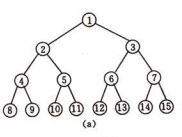
完全二叉树：将深度为k的满二叉树结点进行连续编号。若有结点为n，深度为k,且1~n个结点与满二叉树一一对应的二叉树，称之为完全二叉树。

性质

1. 在二叉树的第i层至多有2^(i-1)个结点
2. 深度为k的二叉树至多有2^k-1个结点
3. 对任何一颗二叉树，如果其终端结点数为n0,度为2的结点数为n2，则n0=n2+1
4. 具有n个结点的完全二叉树的深度为[log2(n)]+1
5. 如果对一棵有n个结点的完全二叉树按层从左到右给结点编号，则对任一结点，有：
   
   • 如果i=1,则结点i为二叉树的根；如果i>1,则其双亲的结点为[i/2]
   • 如果2i>n，则结点i无左孩子；否则其左孩子是结点2i
   • 如果2i+1>n，则结点i无右孩子；否则其右孩子是结点2i+1

遍历

1. 先序遍历：访问根结点，先序遍历左子树，先序遍历友子树。可记口诀：上左右
2. 中序遍历：中序遍历左子树，访问根结点，中序遍历右子树。可记口诀：左上右
3. 后序遍历：后序遍历左子树，后序遍历右子树，访问根结点。可记口诀：左右上

代码

遍历最简单的写法就是递归写法，但递归层数多了时间复杂度会很大，而且仔细思考后，你会发现递归的过程其实就像一个栈后入先出的过程
所以我们可以利用栈写出非递归版的二叉树遍历，这里解释下思路

• 非递归先序：先一路走到最右，边走边输出边压栈，再一个一个弹出的时候去先序遍历右结点
  
  • （1）从根结点开始，一直往左走，边走边压栈且输出结点的
  • （2）当走到终点时，弹出该终点，压入该终结点的右结点。
  • （3）然后从这个右结点再次开始（1）
• 非递归中序：先一路走到最左，边走边压栈。再弹出并且访问它，同时中序遍历它的右结点
  
  • （1）从根结点开始，一直往左走，边走边压栈
  • （2）当走到终点时，弹出该终点，并输出该终点的值。压入该终点的右结点
  • （3）然后从这个右结点再次开始（1）
• 非递归后序：最难的一个遍历。因为要先访问左右结点再访问中结点。办法是根据后序遍历的特质：当一结点有左右结点未访问时不能访问。
  
  • （1）初始化一个只有根结点的栈。
  • （2）判断栈里最上面的结点是否可以访问（即没有左右子树或者左右结点已经访问过）。如果可以访问则访问且弹出该结点，从（2）开始
  • （3）若不能访问，将该结点的右左子结点压入栈，从（2）再开始

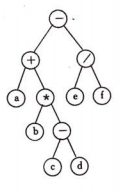
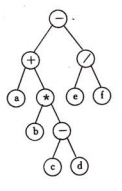
下图为代码中写死的二叉树

import java.util.Stack;

/**
 * 二叉树
 */
public class BinaryTree {
    /** 根结点 */
    public BiTNode root;

    /** 结点 */
    static public class BiTNode {
        public BiTNode lefNode; // 左结点
        public BiTNode riNode; // 右结点
        public String data; // 结点内容

        public BiTNode() {
        }

        public BiTNode(String data) {
            this.data = data;
        }
    }

    /**
     * 默认创造一个写死的二叉树
     */
    public void createBiTree() {
        BiTNode b1 = new BiTNode("-");
        BiTNode b2 = new BiTNode("+");
        BiTNode b3 = new BiTNode("/");
        BiTNode b4 = new BiTNode("a");
        BiTNode b5 = new BiTNode("*");
        BiTNode b6 = new BiTNode("e");
        BiTNode b7 = new BiTNode("f");
        BiTNode b8 = new BiTNode("b");
        BiTNode b9 = new BiTNode("-");
        BiTNode b10 = new BiTNode("c");
        BiTNode b11 = new BiTNode("d");

        this.root = b1;
        b1.lefNode = b2;
        b1.riNode = b3;
        b2.lefNode = b4;
        b2.riNode = b5;
        b3.lefNode = b6;
        b3.riNode = b7;
        b5.lefNode = b8;
        b5.riNode = b9;
        b9.lefNode = b10;
        b9.riNode = b11;
    }

    /**
     * 递归先序，每次都先输出访问结点的内容，再先序遍历左结点，然后右结点
     * 
     * @param rNode
     */
    public void preOrderTraverse(BiTNode rNode) {
        if (rNode == null)
            return;
        System.out.print(rNode.data);
        preOrderTraverse(rNode.lefNode);
        preOrderTraverse(rNode.riNode);
    }

    /**
     * 递归中序，先中序左结点，再输出根结点内容，最后中右结点
     * 
     * @param rNode
     */
    public void inOrderTraverse(BiTNode rNode) {
        if (rNode == null)
            return;
        inOrderTraverse(rNode.lefNode);
        System.out.print(rNode.data);
        inOrderTraverse(rNode.riNode);
    }

    /**
     * 递归后序，后序左结点，后序右结点，输出根结点内容
     * 
     * @param rNode
     */
    public void postOrderTraverse(BiTNode rNode) {
        if (rNode == null)
            return;
        postOrderTraverse(rNode.lefNode);
        postOrderTraverse(rNode.riNode);
        System.out.print(rNode.data);
    }

    /**
     * 非递归先序
     */
    public void preOrder() {
        //建立一个空栈
        Stack<BiTNode> stack = new Stack<BinaryTree.BiTNode>();
        //设置当前结点为根结点
        BiTNode node = root;
        //若当前结点不为空或栈不为空
        while (!stack.isEmpty() || node != null) {
            //一直走到当前结点的最左侧，边走边输出结点值
            while (node != null) {
                //输出结点内容
                System.out.print(node.data);
                //将该结点放入栈
                stack.push(node);
                //设置当前结点为目前结点的左结点
                node = node.lefNode;
            }
            //如果栈未空，弹出栈内结点，设置当前结点为弹出结点的右结点
            if (!stack.isEmpty()) {
                node = stack.pop();
                node = node.riNode;
            }
        }
        System.out.println();
    }

    /**
     * 非递归中序
     */
    public void inOrder() {
        //建立一个空栈
        Stack<BiTNode> stack = new Stack<BinaryTree.BiTNode>();
        //设置当前结点为根结点
        BiTNode node = root;
        //若当前结点不为空或栈不为空
        while (!stack.isEmpty() || node != null) {
            //一直走到当前结点的最左侧，边走边入栈
            while (node != null) {
                stack.push(node);
                node = node.lefNode;
            }
            //如果栈不为空，弹栈，输出弹出结点的值，设置当前结点为弹出结点的右结点
            if (!stack.isEmpty()) {
                node = stack.pop();
                System.out.print(node.data);
                node = node.riNode;
            }
        }
        System.out.println();
    }

    /**
     * 非递归后序
     */
    public void postOrder() {
        //建立一个栈，压入根结点
        Stack<BiTNode> stack = new Stack<BinaryTree.BiTNode>();
        stack.push(root);
        //访问的前一个结点
        BiTNode preNode = null;
        //访问的当前结点
        BiTNode node = null;
        //当栈不为空时
        while (!stack.isEmpty()) {
            //设置当前结点为栈中最后一个压入的结点
            node = stack.lastElement();
            //后序遍历时，一个结点只有左右子树都为空，或者左右结点已经被访问过才会访问它(需要设置一个前结点来确认左右结点是否访问)
            if (node.lefNode == null
                    && node.riNode == null
                    || (preNode != null && (preNode == node.lefNode || preNode == node.riNode))) {
                System.out.print(node.data);
                stack.pop();
                preNode = node;
            }
            //否则，把该结点的左右结点压入栈中
            else {
                //先压右结点入栈
                if (node.riNode != null)
                    stack.push(node.riNode);
                //后压左结点入栈，确保下一次循环的当前结点为左结点
                if (node.lefNode != null)
                    stack.push(node.lefNode);
            }
        }
        System.out.println();
    }

    public static void main(String[] args) {
        BinaryTree binaryTree = new BinaryTree();
        binaryTree.createBiTree();
        System.out.println("先序：");
        binaryTree.preOrderTraverse(binaryTree.root);
        System.out.println();
        binaryTree.preOrder();
        System.out.println("-----------------");
        System.out.println("中序：");
        binaryTree.inOrderTraverse(binaryTree.root);
        System.out.println();
        binaryTree.inOrder();
        System.out.println("-----------------");
        System.out.println("先序：");
        binaryTree.postOrderTraverse(binaryTree.root);
        System.out.println();
        binaryTree.postOrder();
        System.out.println("-----------------");
    }
}/**output:
先序：
-+a*b-cd/ef
-+a*b-cd/ef
-----------------
中序：
a+b*c-d-e/f
a+b*c-d-e/f
-----------------
先序：
abcd-*+ef/-
abcd-*+ef/-
-----------------
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214