matlab求解普通函数的导数问题（diff函数的用法）_matlab什么函数可以解基本函数导数

一元函数的导数

MATLAB函数语法

y = diff(fun, x)        % // 函数fun的一阶导数
y = diff(fun, x, n)     % // 函数fun的 n阶导数
1
2

注：自变量为唯一符号变量时，可以省去$x$。

应用举例

例1 ：普通函数求导

给定函数$$f(x)=\frac{sinx}{x^2+4x+3}$$分别求其一阶导数和四阶导数，并绘制原函数和一阶导数的图像，计算求解50阶导数时所用的时间。

syms x; f=sin(x)/(x^2+4*x+3); f1=diff(f)
ezplot(f,[0,5]), hold on; ezplot(f1,[0,5])
f4 = diff(f,x,4)
f41 = collect(simplify(f4),sin(x))
f42 = collect(simplify(f4),cos(x))
tic, diff(f,x,50); toc
1
2
3
4
5
6

根据结果可知diff函数的效率较高。

例2 ：复合泛函求导

已知函数$F(t)=t^2\ast sint\ast f(t)$，推导其三阶导数公式。

分析：该题难点为如何定义$f(t)$

syms t f(t)
G = simplify(diff(t^2*sin(t)*f,t,3))
1
2

当$f(t)=e^{-t}$时，$F(t)$的三阶导数为

G0 = simplify(subs(G,f,exp(-t)))
err = simplify(diff(t^2*sin(t)*exp(-t),3)-G0)
1
2

例3 ：矩阵函数求导

对每个矩阵元素直接求导

syms x; 
H=[4*sin(5*x), exp(-4*x^2); 3*x^2+4*x+1, sqrt(4*x^2+2)], 
H1=diff(H,x,3)
1
2
3

多元函数的偏导数

MATLAB函数语法

高阶偏导数的求法

y = diff(diff(fun, x, m), y, n)       
y = diff(diff(fun, y, n), x, m)   
1
2

应用举例

例1 ：求偏导并绘图

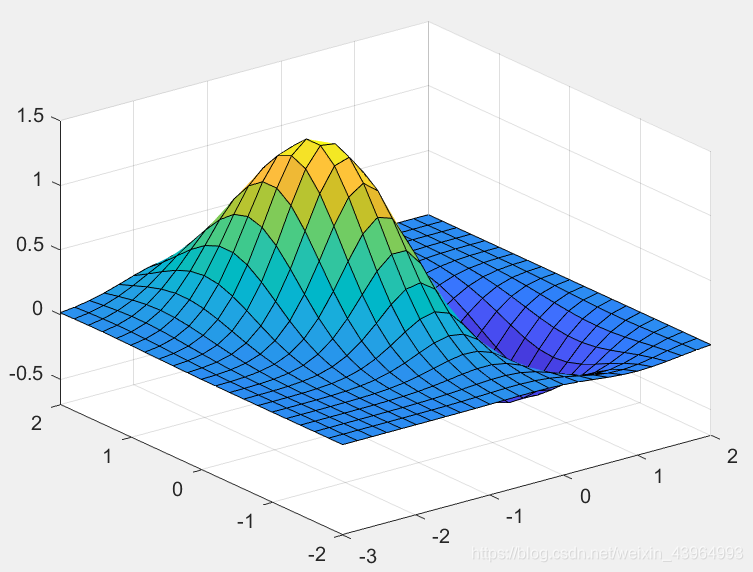
求函数$z=f(x,y)=(x^2-2x)e^{-x^2-y^2-xy}$的一阶偏导数$\partial z/\partial x,\partial z/\partial y$,并绘图。

• 求偏导数

syms x y
z  = (x^2-2*x)*exp(-x^2-y^2-x*y);
zx = simplify(diff(z,x))
zy = simplify(diff(z,y))
1
2
3
4

• 绘制三维曲面

[x0,y0] = meshgrid(-3:.2:2,-2:.2:2); 
z0 = double(subs(z,{x,y},{x0,y0}));
surf(x0,y0,z0), zlim([-0.7 1.5]) 
1
2
3

• 绘制引力线（负梯度）

contour(x0,y0,z0,30), hold on
zx0 = subs(zx,{x,y},{x0,y0}); 
zy0 = subs(zy,{x,y},{x0,y0}); 
quiver(x0,y0,-zx0,-zy0)
1
2
3
4

例2 ：三元函数求偏导

求函数$f(x,y,z)=sin(x^{2}y)e^{-x^{2}y-z^2}$的偏导数${\partial }^{4}f(x,y,z)/(\partial x^2\partial y\partial z)$

syms x y z
f  = sin(x^2*y)*exp(-x^2*y-z^2); 
df = diff(diff(diff(f,x,2),y),z); 
df = simplify(df)
1
2
3
4