01背包问题（通俗易懂，图例讲解）

问题描述：

01背包问题：一个容量为c的背包，现有n个物品可供选择。物品 i 的重量似乎 wi，其价值为 vi，如何选择放入背包的物品，使得背包中的物品总价值最大？ 

01背包问题是一种动态规划问题。动态规划的核心就是状态转移方程，下面我们就用简单的例子来解决这个问题：

动态规划展示：

假设有3种水果可供选择：                   重量    价值                       背包重量为4kg

                                                榴莲      1kg     150元

                                                菠萝      3kg      200元

                                                草莓      4kg      400元

我们可以先从1kg背包开始算起，然后逐步到4kg背包。

下面我们来画图表来展示，横向代表背包重量，纵向代表水果种类；

 

我们先从第一行开始填，填完整后就找到了我们想要的结果；

第一行也就是我们需要将榴莲装入背包中，第一个格子是1kg的背包，而榴莲正好也是1kg，那我们就可以把它装进包里，价值为150元；

第二个单元格是2kg的背包，也可以装下1kg的榴莲，后面几个也一样，3kg的背包也装得下榴莲，现在你会觉得3kg背包也可以装下菠萝（3kg），但是现在我们考虑的只是第一行， 只有榴莲，可以这么理解现在只有榴莲可以放入背包，其他的水果都没有；所以3kg，4kg的背包都是装榴莲（1kg），其价值是150元。

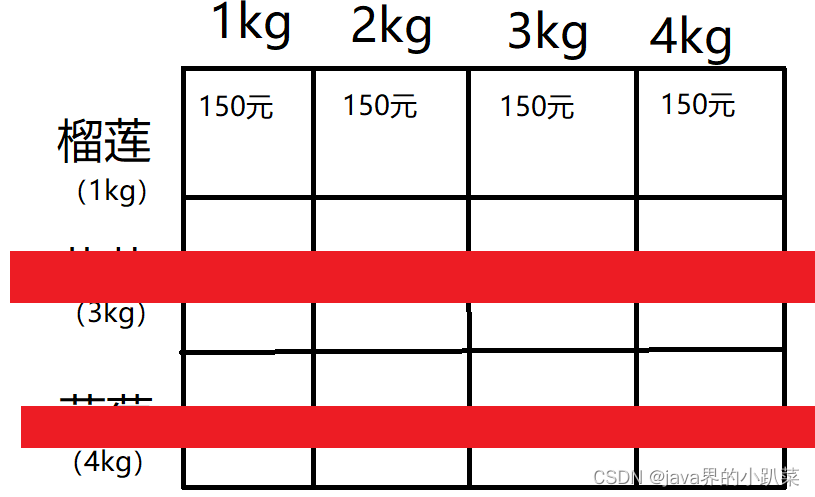
 此时背包装的东西的最大价值是150元，这只是代表的只有榴莲的情况下的最大价值，也就是说只有榴莲的情况下，背包装的东西的最大价值是150元。

下面我们再加入菠萝，也就是说此时有榴莲，菠萝两种水果可以进行选择，现在我们继续计算：

因为菠萝重量为3kg，所以在第二行第一列（1kg背包）此处装不下菠萝，只能装榴莲，所以背包装榴莲，价值150元；

 

 同理，2kg的背包也装不下菠萝，所以2kg背包最大价值也是150元榴莲；

3kg背包可以装菠萝，也可以装榴莲，但菠萝价值大于榴莲价值，所以3kg背包装菠萝，最大价值为200元；

 

4kg背包可以同时装下榴莲和菠萝，其最大价值为350元；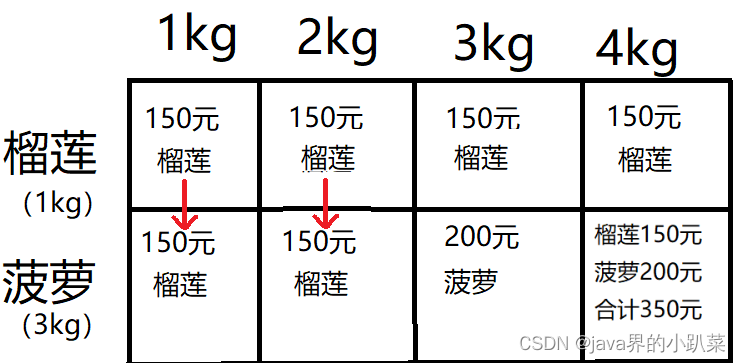

然后我们继续加入草莓来计算 ：

1-3kg背包和上面一样

 

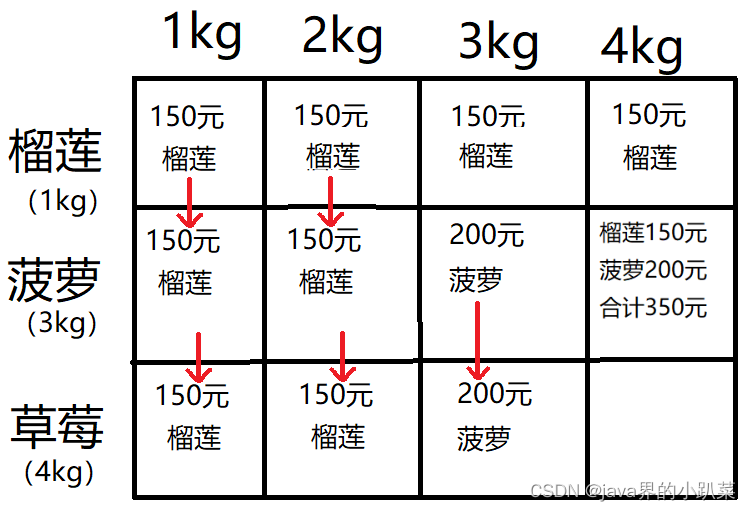
 4kg背包有多种选择，一种是榴莲+菠萝组合，一种是草莓，

榴莲+菠萝 价值为350元，草莓价值为400元，所以4kg背包最大价值为400元，只装草莓；

 所以最终答案为装草莓，其最大价值为400元。

 逻辑分析

 

 上面的分析，其实都可以用这个公式来计算，当前单元格的值等于两个值相比的最大值，比如最后的结果，我们用上面单元格的350与当前商品的价格400+剩余空间可用价值0（因为没有可用空间了）相比，取最大值400；

再比如菠萝行4kg背包那个单元格的值等于：它上面单元格的值150与当前商品价格200+剩余空间可用价值（cell[1][4-3]=cell[1][1]=150）的和350元相比，取最大值350元。

 代码实现

      public static void main(String[] args) {
            Scanner scan = new Scanner(System.in);
            String str_0 = scan.nextLine();
            String[] line_list_0 = str_0.trim().split(" ");
            ArrayList<Integer> arr_temp = new ArrayList<>();
            for(int i = 0; i < line_list_0.length; i++){
                arr_temp.add(Integer.parseInt(line_list_0[i]));
            }
 
 
            int c = arr_temp.get(0);
            int n = arr_temp.get(1);
 
 
            ArrayList<ArrayList<Integer>> vector = new ArrayList<>();
            for(int i = 0; i < n; i++){
                String str_2 = scan.nextLine();
                String[] line_list_2 = str_2.trim().split(" ");
                ArrayList<Integer> temp_2 = new ArrayList<>();
                for(int j = 0; j < line_list_2.length; j++){
                    temp_2.add(Integer.parseInt(line_list_2[j]));
                }
                vector.add(temp_2);
            }
 
 
            scan.close();
 
            int result = solution(c, n, vector);
 
            System.out.println(result);
 
 
        }
 
    public static int solution(int c, int n, ArrayList<ArrayList<Integer>> vector) {
        //n物品个数 c背包容量
        int weight[] = new int[n];//物品重量
        int value[] = new int[n];//物品价值
        for(int i=0;i<n;i++)
        {
            weight[i]=vector.get(i).get(0);
            value[i]=vector.get(i).get(1);
        }
 
        // 构造最优解的网格:3行4列
        int[][] maxValue = new int[n][c];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < c; j++) {
                maxValue[i][j] = 0;
            }
        }
 
        // 填充网格
        for (int i = 0; i < n; i++) {
            for (int j = 1; j <= c; j++) {
                if (i == 0) {
                    maxValue[i][j - 1] = (weight[i] <= j ? value[i] : 0);
                } else {
                    int topValue = maxValue[i - 1][j - 1];  // 上一个网格的值
                    int thisValue = (weight[i] <= j ?       // 当前商品的价值 + 剩余空间的价值
                            (j - weight[i] > 0 ? value[i] + maxValue[i - 1][j - weight[i]] : value[i])
                            : topValue);
 
                    // 返回 topValue和thisValue中较大的一个
                    maxValue[i][j - 1] = (topValue > thisValue ? topValue : thisValue);
                }
            }
        }
        return maxValue[n-1][c-1];
    }

有问题的可以留言询问

欢迎转载，转载请注明出处。