Python处理双11购物的凑单问题与财务凑数问题_python使用参数求双十一减满折扣

大家好，我是强哥。

今天分享一篇用python处理双11购物的凑单问题与财务凑数问题的文章。

---

凑单问题

对于各类凑单问题，最经典的就是淘宝双十一的满减促销活动，比如“满 200 元减 50 元”。假设你的购物车中有 n 个（n>100）想买的商品，希望从里面选几个，在凑够满减条件的前提下，让选出来的商品价格总和最大程度地接近满减条件（200 元），如何编程解决这个问题？

动态规划解决

使用传统的编程思路就是使用动态规划，思路如下：

购物车中有 n 个商品，针对每个商品都决策是否购买。每次决策之后，对应不同的状态集合。用一个二维数组 s t a t e s [ n ] [ x ] states[n][x] states[n][x]，来记录每次决策之后所有可达的状态。

python实现代码为：

def double11advance(items_info: list, w: int):  
    """  
    动态规划解决双11凑单问题  
    :param items_info: 每个商品价格  
    :param w: 满减条件，比如 200  
    :return:  
    """  
    n = len(items_info)  
    # 超过 3 倍就没有薅羊毛的价值了  
    states = [[False] * (3 * w + 1) for i in range(n)]  
    states[0][0] = True  
    states[0][items_info[0]] = True  
    for i in range(1, n):  
        for j in range(3 * w + 1):  
            if states[i - 1][j]:  
                # 不购买第i个商品  
                states[i][j] = states[i - 1][j]  
                # 购买第i个商品  
                nw = j + items_info[i]  
                if nw <= 3 * w:  
                    states[i][nw] = True  
    j = w  
    while j < 3 * w + 1 and not states[n - 1][j]:  
        j += 1  
    # j是大于等于 w 的最小值  
    if j == 3 * w + 1:  
        return  # 没有可行解  
    idx = []  
    for i in range(n - 1, 0, -1):  
        if j - items_info[i] >= 0 and states[i - 1][j - items_info[i]]:  
            idx.append(i)  
            j -= items_info[i]  
    if j != 0:  
        idx.append(0)  
    return sorted(idx)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

假设，我们的购物车中每件商品的价格为：

48, 30, 19, 36, 36, 27, 42, 42, 36, 24,  40, 70, 32  

1
2

我们执行代码：

import numpy as np  
items_info = np.array([48, 30, 19, 36, 36, 27, 42, 42, 36, 24,  40, 70, 32])  
  
idx = double11advance(items_info, 200)  
print("选中商品的索引：", idx)  
print("选中商品的价格：", items_info[idx])  
print("总价格：", sum(items_info[idx]))
1
2
3
4
5
6
7

选中商品的索引： [1, 4, 7, 8, 9, 12]  
选中商品的价格： [30 36 42 36 24 32]  
总价格：200
1
2
3

可以看到程序完美的找到了一组可行解。

除了动态规划，我们还可以使用回溯算法解决，参考代码就不公布了，接下来我们直接使用优化算法解决这个问题。

优化算法解决

在前面的文章《OR-Tools官档中文用法大全（CP、LP、VRP、Flows等）https://xxmdmst.blog.csdn.net/article/details/124203863》中的 背包与装箱问题 一章中，我演示了使用SCIP求解器解决该问题。

不过SCIP求解器速度较慢，而且想获取多个可行解实现起来较为麻烦，所以这里我演示使用ortools的cp_model求解器来解决该问题。

cp_model求解器相对于前面的SCIP求解器的缺点在于只能处理整数。

代码如下：

from ortools.sat.python import cp_model  
import numpy as np  
  
model = cp_model.CpModel()  
items_info = np.array([48, 30, 19, 36, 36, 27, 42, 42, 36, 24,  40, 70, 32])  
items = np.arange(items_info.shape[0])  
x = [model.NewBoolVar(f'x_{i}') for i in range(len(items_info))]  
obj = (x*items_info).sum()  
model.Add(obj >=200)  
model.Minimize(obj)  
solver = cp_model.CpSolver()  
status = solver.Solve(model)  
result = [bool(solver.Value(i)) for i in x]  
print("选中商品的索引：", items[result])  
print("选中商品的价格：", items_info[result])  
print("总价格：", items_info[result].sum())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

选中商品的索引： [ 1  4  7  8  9 12]  
选中商品的价格： [30 36 42 36 24 32]  
总价格：200
1
2
3

可以看到 ortools 库得到了与前面动态规划一致的结果。

ortools获取多个可行解

下面我们考虑使用cp_model求解器获取多个可行解，前面我们已经可行解的最小值为200，下面我们可以限制总价格等于200：

from ortools.sat.python import cp_model  
import numpy as np  
  
  
class MyCpSolver(cp_model.CpSolverSolutionCallback):  
    def __init__(self, x):  
        cp_model.CpSolverSolutionCallback.__init__(self)  
        self.x = x  
        self.num = 0  
  
    def on_solution_callback(self):  
        self.num += 1  
        print(f"第{self.num}个解")  
        result = [bool(self.Value(i)) for i in self.x]  
        print("选中商品的索引：", items[result])  
        print("选中商品的价格：", items_info[result])  
        print("总价格：", items_info[result].sum())  
  
  
model = cp_model.CpModel()  
items_info = np.array([48, 30, 19, 36, 36, 27, 42, 42, 36, 24,  40, 70, 32])  
items = np.arange(items_info.shape[0])  
x = [model.NewBoolVar(f'x_{i}') for i in range(len(items_info))]  
obj = (x*items_info).sum()  
model.Add(obj == 200)  
solver = cp_model.CpSolver()  
myCpSolver = MyCpSolver(x)  
solver.parameters.enumerate_all_solutions = True  
status = solver.Solve(model, myCpSolver)  
print(solver.StatusName(status))  
print("解的个数：", myCpSolver.num)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

最终得到了30个可行解：

如此多的可行解是因为36出现了三次，导致可行解的个数也被翻了3倍，实际可行解就只有10个。下面我们改进一下上面代码，让其获取唯一的可行解：

from collections import Counter  
from ortools.sat.python import cp_model  
import numpy as np  
  
  
class MyCpSolver(cp_model.CpSolverSolutionCallback):  
    def __init__(self, x):  
        cp_model.CpSolverSolutionCallback.__init__(self)  
        self.x = x  
        self.num = 0  
  
    def on_solution_callback(self):  
        self.num += 1  
        print(f"第{self.num}个解")  
        idx = []  
        result = []  
        for i, xi in enumerate(self.x):  
            v = self.Value(xi)  
            if v == 0:  
                continue  
            idx.append(i)  
            result.extend([items_info[i]]*v)  
        print("选中商品的索引：", idx)  
        print("选中商品的价格：", result)  
        print("总价格：", sum(result))  
  
  
arr = [48, 30, 19, 36, 36, 27, 42, 42, 36, 24,  40, 70, 32]  
  
model = cp_model.CpModel()  
items_info = []  
x = []  
for i, (k, v) in enumerate(Counter(arr).items(), 1):  
    items_info.append(k)  
    x.append(model.NewIntVar(0, v, f"x{i}"))  
items_info = np.array(items_info)  
obj = (items_info*x).sum()  
model.Add(obj == 200)  
solver = cp_model.CpSolver()  
myCpSolver = MyCpSolver(x)  
solver.parameters.enumerate_all_solutions = True  
status = solver.Solve(model, myCpSolver)  
print(solver.StatusName(status))  
print("解的个数：", myCpSolver.num)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

第1个解  
选中商品的索引： [1, 2, 4, 5, 7]  
选中商品的价格： [30, 19, 27, 42, 42, 40]  
总价格：200  
第2个解  
选中商品的索引： [2, 3, 4, 5, 7]  
选中商品的价格： [19, 36, 36, 27, 42, 40]  
总价格：200  
第3个解  
选中商品的索引： [2, 4, 5, 8]  
选中商品的价格： [19, 27, 42, 42, 70]  
总价格：200  
第4个解  
选中商品的索引： [0, 2, 3, 4, 8]  
选中商品的价格： [48, 19, 36, 27, 70]  
总价格：200  
第5个解  
选中商品的索引： [0, 2, 4, 5, 6, 7]  
选中商品的价格： [48, 19, 27, 42, 24, 40]  
总价格：200  
第6个解  
选中商品的索引： [0, 1, 2, 3, 4, 7]  
选中商品的价格： [48, 30, 19, 36, 27, 40]  
总价格：200  
第7个解  
选中商品的索引： [0, 5, 7, 8]  
选中商品的价格： [48, 42, 40, 70]  
总价格：200  
第8个解  
选中商品的索引： [1, 3, 6, 7, 8]  
选中商品的价格： [30, 36, 24, 40, 70]  
总价格：200  
第9个解  
选中商品的索引： [1, 3, 5, 6, 9]  
选中商品的价格： [30, 36, 36, 42, 24, 32]  
总价格：200  
第10个解  
选中商品的索引： [0, 3, 5, 9]  
选中商品的价格： [48, 36, 42, 42, 32]  
总价格：200  
OPTIMAL  
解的个数：10
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

可以看到顺利的获取到唯一解。

财务凑数问题

财务凑数问题与前面的问题模型一致，区别在于存在小数，例如从一大批金额中找出能够合并出指定金额的组合。

假设我们要查找的金额列表如下：

7750.0, 50000.0, 94693.0, 89159.18, 59000.0, 19634.94, 27000.0, 37770.17, 55631.64, 23800.0,  
20000.0, 20000.0, 20000.0, 72985.45, 48000.0, 48000.0, 58750.0, 22000.0, 11219.61, 45600.0,  
90500.0, 84288.0, 930.0, 1352.0, 120.0, 750.0, 22880.0, 45678.0, 49555.0, 17181.54, 1925.0,  
1500.0, 83325.0, 500.0, 1298.5, 36936.34, 91933.67, 5205.0, 20195.0, 20550.0, 10600.0, 3200.0,  
6400.0, 6900.0, 9900.0, 9750.0, 9600.0, 7200.0, 15208.41, 10550.0, 21077.02, 75437.51, 73515.11,  
3140.0, 85128.6, 87095.74, 22806.24, 961.72, 13285.47, 28980.0, 67997.62, 35955.33, 12890.27, 15459.47,  
20124.58, 25246.66, 13216.11, 89400.0, 89400.0, 26800.0, 11365.0, 16457.0, 50000.0, 54309.0, 12000.0,  
39000.0, 70569.5, 45231.5, 56400.0, 86400.0, 86400.0, 86400.0, 86400.0, 12000.0, 390.0, 2500.0, 38109.79,  
5968.63, 14862.6, 45038.91, 63189.17, 80784.86, 37664.87, 4981.44, 50000.0, 50000.0, 32323.01, 567.73, 66056.88, 26400.0
1
2
3
4
5
6
7
8
9

我们需要找到95984的组合。

SCIP求解器直接计算

如果使用SCIP求解器可以直接计算结果，编码如下：

from ortools.linear_solver import pywraplp  
import numpy as np  
  
arr = [7750.0, 50000.0, 94693.0, 89159.18, 59000.0, 19634.94, 27000.0, 37770.17, 55631.64, 23800.0,  
       20000.0, 20000.0, 20000.0, 72985.45, 48000.0, 48000.0, 58750.0, 22000.0, 11219.61, 45600.0,  
       90500.0, 84288.0, 930.0, 1352.0, 120.0, 750.0, 22880.0, 45678.0, 49555.0, 17181.54, 1925.0,  
       1500.0, 83325.0, 500.0, 1298.5, 36936.34, 91933.67, 5205.0, 20195.0, 20550.0, 10600.0, 3200.0,  
       6400.0, 6900.0, 9900.0, 9750.0, 9600.0, 7200.0, 15208.41, 10550.0, 21077.02, 75437.51, 73515.11,  
       3140.0, 85128.6, 87095.74, 22806.24, 961.72, 13285.47, 28980.0, 67997.62, 35955.33, 12890.27, 15459.47,  
       20124.58, 25246.66, 13216.11, 89400.0, 89400.0, 26800.0, 11365.0, 16457.0, 50000.0, 54309.0, 12000.0,  
       39000.0, 70569.5, 45231.5, 56400.0, 86400.0, 86400.0, 86400.0, 86400.0, 12000.0, 390.0, 2500.0, 38109.79,  
       5968.63, 14862.6, 45038.91, 63189.17, 80784.86, 37664.87, 4981.44, 50000.0, 50000.0, 32323.01, 567.73, 66056.88, 26400.0]  
  
items_info = np.array(arr)  
items = np.arange(items_info.shape[0])  
solver = pywraplp.Solver.CreateSolver('SCIP')  
x = [solver.BoolVar(f'x_{i}') for i in range(len(items_info))]  
obj = (x*items_info).sum()  
solver.Add(obj >= 95984)  
solver.Minimize(obj)  
status = solver.Solve()  
print("总重量：", obj.solution_value())  
result = np.frompyfunc(lambda x: x.solution_value(), 1, 1)(x).astype(bool)  
print("选中商品的索引：", items[result])  
print("选中商品的价值：", items_info[result])  
print("总价值：", items_info[result].sum())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

总重量：95984.3  
选中商品的索引： [22 24 33 34 38 40 41 44 58 61]  
选中商品的价值： [  930.     120.     500.    1298.5  20195.   10600.    3200.    9900.  
 13285.47 35955.33]  
总价值：95984.3
1
2
3
4
5

不过这并不是真正的最优解，如果我们把约束设置为必须为目标值：

solver = pywraplp.Solver.CreateSolver('SCIP')  
x = [solver.BoolVar(f'x_{i}') for i in range(len(items_info))]  
obj = (x*items_info).sum()  
solver.Add(obj == 95984)  
status = solver.Solve()  
print("总重量：", obj.solution_value())  
result = np.frompyfunc(lambda x: x.solution_value(), 1, 1)(x).astype(bool)  
print("选中商品的索引：", items[result])  
print("选中商品的价值：", items_info[result])  
print("总价值：", items_info[result].sum())
1
2
3
4
5
6
7
8
9
10

总重量：95984.0  
选中商品的索引： [ 5 18 25 30 38 39 43 45 53 57 84 97]  
选中商品的价值： [19634.94 11219.61   750.    1925.   20195.   20550.    6900.    9750.  
  3140.     961.72   390.     567.73]  
总价值：95984.0
1
2
3
4
5

可惜耗时接近10秒。

cp_model求解器

cp_model求解器只能处理整数，为了能够处理小数，我们可以将其乘以100后转换为整数：

from ortools.sat.python import cp_model  
import numpy as np  
  
arr = [7750.0, 50000.0, 94693.0, 89159.18, 59000.0, 19634.94, 27000.0, 37770.17, 55631.64, 23800.0,  
       20000.0, 20000.0, 20000.0, 72985.45, 48000.0, 48000.0, 58750.0, 22000.0, 11219.61, 45600.0,  
       90500.0, 84288.0, 930.0, 1352.0, 120.0, 750.0, 22880.0, 45678.0, 49555.0, 17181.54, 1925.0,  
       1500.0, 83325.0, 500.0, 1298.5, 36936.34, 91933.67, 5205.0, 20195.0, 20550.0, 10600.0, 3200.0,  
       6400.0, 6900.0, 9900.0, 9750.0, 9600.0, 7200.0, 15208.41, 10550.0, 21077.02, 75437.51, 73515.11,  
       3140.0, 85128.6, 87095.74, 22806.24, 961.72, 13285.47, 28980.0, 67997.62, 35955.33, 12890.27, 15459.47,  
       20124.58, 25246.66, 13216.11, 89400.0, 89400.0, 26800.0, 11365.0, 16457.0, 50000.0, 54309.0, 12000.0,  
       39000.0, 70569.5, 45231.5, 56400.0, 86400.0, 86400.0, 86400.0, 86400.0, 12000.0, 390.0, 2500.0, 38109.79,  
       5968.63, 14862.6, 45038.91, 63189.17, 80784.86, 37664.87, 4981.44, 50000.0, 50000.0, 32323.01, 567.73, 66056.88, 26400.0]  
model = cp_model.CpModel()  
items_info = (np.array(arr)*100).astype(int)  
items = np.arange(items_info.shape[0])  
x = [model.NewBoolVar(f'x_{i}') for i in range(len(items_info))]  
obj = (x*items_info).sum()  
model.Add(obj == 95984*100)  
solver = cp_model.CpSolver()  
status = solver.Solve(model)  
print(solver.StatusName(status))  
result = [bool(solver.Value(i)) for i in x]  
print("选中商品的索引：", items[result])  
print("选中商品的价格：", items_info[result]/100)  
print("总价格：", items_info[result].sum()/100)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

OPTIMAL  
选中商品的索引： [ 0 23 24 41 42 47 53 70 71 75]  
选中商品的价格： [ 7750.  1352.   120.  3200.  6400.  7200.  3140. 11365. 16457. 39000.]  
总价格：95984.0
1
2
3
4

获取多个可行解

可以看到财务的金额数据存在大量重复，所以必须先进行计数处理，最终代码为：

from collections import Counter  
from ortools.sat.python import cp_model  
import numpy as np  
  
  
class MyCpSolver(cp_model.CpSolverSolutionCallback):  
    def __init__(self, x):  
        cp_model.CpSolverSolutionCallback.__init__(self)  
        self.x = x  
        self.num = 0  
  
    def on_solution_callback(self):  
        self.num += 1  
        print(f"第{self.num}个解")  
        idx = []  
        result = []  
        for i, xi in enumerate(self.x):  
            v = self.Value(xi)  
            if v == 0:  
                continue  
            idx.append(i)  
            result.extend([items_info[i]/100]*v)  
        print("选中商品的索引：", idx)  
        print("选中商品的价格：", result)  
        print("总价格：", sum(result))  
  
  
arr = [7750.0, 50000.0, 94693.0, 89159.18, 59000.0, 19634.94, 27000.0, 37770.17, 55631.64, 23800.0,  
       20000.0, 20000.0, 20000.0, 72985.45, 48000.0, 48000.0, 58750.0, 22000.0, 11219.61, 45600.0,  
       90500.0, 84288.0, 930.0, 1352.0, 120.0, 750.0, 22880.0, 45678.0, 49555.0, 17181.54, 1925.0,  
       1500.0, 83325.0, 500.0, 1298.5, 36936.34, 91933.67, 5205.0, 20195.0, 20550.0, 10600.0, 3200.0,  
       6400.0, 6900.0, 9900.0, 9750.0, 9600.0, 7200.0, 15208.41, 10550.0, 21077.02, 75437.51, 73515.11,  
       3140.0, 85128.6, 87095.74, 22806.24, 961.72, 13285.47, 28980.0, 67997.62, 35955.33, 12890.27, 15459.47,  
       20124.58, 25246.66, 13216.11, 89400.0, 89400.0, 26800.0, 11365.0, 16457.0, 50000.0, 54309.0, 12000.0,  
       39000.0, 70569.5, 45231.5, 56400.0, 86400.0, 86400.0, 86400.0, 86400.0, 12000.0, 390.0, 2500.0, 38109.79,  
       5968.63, 14862.6, 45038.91, 63189.17, 80784.86, 37664.87, 4981.44, 50000.0, 50000.0, 32323.01, 567.73, 66056.88, 26400.0]  
  
model = cp_model.CpModel()  
items_info = []  
x = []  
for i, (k, v) in enumerate(Counter(arr).items(), 1):  
    items_info.append(k)  
    x.append(model.NewIntVar(0, v, f"x{i}"))  
items_info = (np.array(items_info)*100).astype(int)  
obj = (items_info*x).sum()  
model.Add(obj == 95984*100)  
solver = cp_model.CpSolver()  
myCpSolver = MyCpSolver(x)  
solver.parameters.enumerate_all_solutions = True  
status = solver.Solve(model, myCpSolver)  
print(solver.StatusName(status))  
print("解的个数：", myCpSolver.num)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

最终再经过一小时的等待后，并未找出全部的可行解，程序还在运行中，1小时找到一千多个可行解：

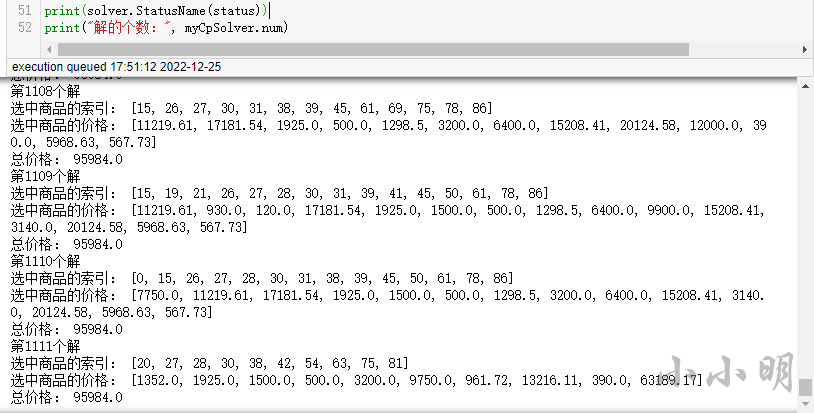
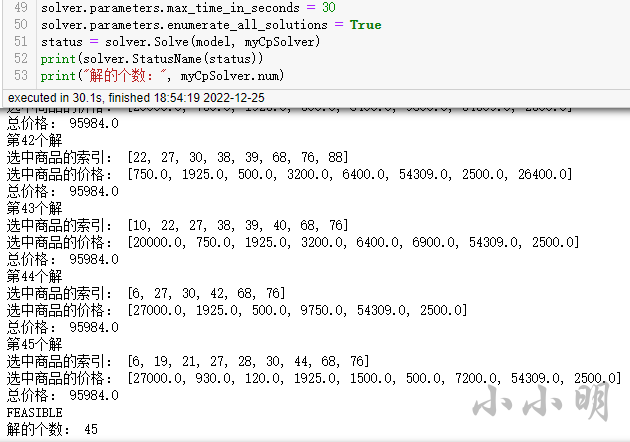
为了避免计算时间过长，我们可以设置最大执行时间，例如设置30秒：

solver.parameters.max_time_in_seconds = 30  

1
2

可以看到30秒内能够找到45个解：

感兴趣的小伙伴，赠送全套Python学习资料，包含面试题、简历资料等具体看下方。

一、Python所有方向的学习路线

Python所有方向的技术点做的整理，形成各个领域的知识点汇总，它的用处就在于，你可以按照下面的知识点去找对应的学习资源，保证自己学得较为全面。

二、Python必备开发工具

工具都帮大家整理好了，安装就可直接上手！

三、最新Python学习笔记

当我学到一定基础，有自己的理解能力的时候，会去阅读一些前辈整理的书籍或者手写的笔记资料，这些笔记详细记载了他们对一些技术点的理解，这些理解是比较独到，可以学到不一样的思路。

四、Python视频合集

观看全面零基础学习视频，看视频学习是最快捷也是最有效果的方式，跟着视频中老师的思路，从基础到深入，还是很容易入门的。

五、实战案例

纸上得来终觉浅，要学会跟着视频一起敲，要动手实操，才能将自己的所学运用到实际当中去，这时候可以搞点实战案例来学习。

六、面试宝典

简历模板

若有侵权，请联系删除