热门标签
热门文章
- 1深度学习(11)之Anchor-Free详解
- 2算法训练营第六十九天 | 并查集理论基础、寻找存在的路径、冗余连接、冗余连接II_卡码网
- 3Git常用命令大全_git rename
- 4弹出框 custombox.min.js 使用时候由于滚动条隐藏造成网页抖动变形的解决办法
- 5【前端系列】20种 Button 样式_前端按钮
- 6uniapp:完成商品分类页面(scroll-view),左侧导航,右侧商品_uniapp左侧导航右侧内容
- 7深度学习实战—基于TensorFlow 2.0的人工智能开发应用_深度学习实战:基于tensorflow
- 8QT网络编程之实现TCP客户端和服务端_qt tcp客户端
- 9哈工大(HIT)计算机网络 翻转课堂 实验 mooc答案 总结_哈工大计网mooc答案
- 10Stable Diffusion学习笔记_马尔科夫链的反向过程是
当前位置: article > 正文
人工智能---A*算法_a*人工智能
作者:你好赵伟 | 2024-07-04 11:29:40
赞
踩
a*人工智能
实验目的
- 以八数码问题作为对象, 利用A*算法求解并在屏幕上动态显示OPEN表的结点和评估函
数最小的结点
实验内容
- 使用两种启发式函数并比较两者的不同之处。
实验器材
语言: Python、编译器: PyCharm
实验过程与结果
- 这是一个八数码问题,也就是一个3× 3的九宫格打乱之后的恢复问题,其中空格我们可以用数字0补全,这样方便与自己编程。 首先的第一个问题也就是能否到达目标状态的,可以通过资料查阅得到的条件是: 初始状态与目标状态的逆序和的奇偶性一样也就可以恢复初始状态(对于所有的奇数的数码问题都是如此)
- 所以这一部分的代码如下:
# 计算逆序和 # 计算逆序和 def calculat_inverse(arr): inverse_sum = 0 n = len(arr) m = n ** 2 - 1 for i in range(n ** 2): temp = [k + 1 for k in range(i, m - 1)] for j in temp: if arr[int(j / n), j % n] == 0: continue elif arr[int(i / n), i % n] > arr[int(j / n), j % n]: inverse_sum = inverse_sum + 1 return inverse_sum # 判断是否能够到达目的状态 # 用于判断是否有解 def judge(start, target_state): return (calculat_inverse(start) % 2) == (calculat_inverse(target_state) % 2)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 两种启发函数(因为一个是八数码一个是九数码问题,其中九数码问题在于将0也算入评估函数之中,所以就会有4个,尽管八数码与九数码只是细微上的区别)
# 九数码 # 评估函数2 # 放错元素与正确位置的曼哈顿距离 # 返回一个数字 def evaluate2(current, target_state): distances = 0 # 如果是八数码为题则改为 arange(1, 9, 1, dtype=int) for i in arange(0, 9, 1, dtype=int): index_1 = argwhere(current == i) index_2 = argwhere(target_state == i) distances = distances + (abs(index_1[0][0] - index_2[0][0]) + abs(index_1[0][1] - index_2[0][1])) return distances # 九数码 # 评估函数1 # 放错位置的元素的个数 # 返回一个数字 def evaluate(current, target_state): temp = current - target_state count = 0 ''' 如果是八数码问题则改为: result = sum(temp != 0) if result > len(current)**2 - 1: result = len(current)**2 - 1 return result ''' return sum(temp != 0) # 八数码 # 评估函数3 八数码问题 # 放错位置的元素的个数 # 返回一个数字 def evaluate3(current, target_state): temp = current - target_state result = sum(temp != 0) if result > len(current)**2 - 1: result = len(current)**2 - 1 return result # 八数码 # 评估函数4 # 放错元素与正确位置的哈密顿距离 # 返回一个数字 def evaluate4(current, target_state): distances = 0 for i in arange(1, 9, 1, dtype=int): index_1 = argwhere(current == i) index_2 = argwhere(target_state == i) distances = distances + (abs(index_1[0][0] - index_2[0][0]) + abs(index_1[0][1] - index_2[0][1])) return distances # 判断是否在状态表中 def checkadd(states, b, n): for i in range(n): if str(states[i]) == str(b): return i return -1 # 算法核心 def a_start(states, current, target_state, tag): # 根据tag选择对应的评估函数 if tag == 1: method = evaluate elif tag == 2: method = evaluate2 elif tag == 3: method = evaluate3 elif tag == 4: method = evaluate4 path = zeros([maxsize], dtype=uint) # 记录是否访问过 visited = array([False for i in range(maxsize)]) # 估计函数值 evaluate_value = array([0 for i in range(maxsize)]) # 路径的长度 depth = array([0 for i in range(maxsize)]) # 记录状态的变换 curpos = copy.deepcopy(current) id, curid = 0, 0 evaluate_value[id] = method(curpos, target_state) states[id] = current id = id + 1 # 访问的节点的个数 count = 0 # 判断状态是否相同 while not str(curpos) == str(target_state): for i in range(1, 5): tmp = move(curpos, i) # 判断是否移动成功 if tmp[1]: state = checkadd(states, tmp[0], id) print("当前层数", depth[curid]) print("前一代的评估值", method(curpos, target_state)) print("当前的评估值", method(tmp[0], target_state)) # 不在表中,存入表中 if state == -1: count = count + 1 path[id] = curid depth[id] = depth[curid] + 1 evaluate_value[id] = method(tmp[0], target_state) + depth[id] states[id] = tmp[0] id = id + 1 # 在表中,进行更新 else: l = depth[curid] + 1 fit = method(tmp[0], target_state) + l if fit < evaluate_value[state]: path[state] = curid depth[state] = l evaluate_value[state] = fit visited[curid] = True min_eval = -1 # 取出最小的节点 open_count = 0 for i in range(id): if visited[i] == False and (min_eval == -1 or evaluate_value[i] < evaluate_value[min_eval]): open_count += 1 min_eval = i curid = min_eval curpos = states[curid] print("当前open表的数目是:", open_count) print("当前总的结点数目是:", count) print("当前最小的节点评估值是:", evaluate_value[curid], "当前最小的节点是") print(states[curid]) print("+"*100) if id == maxsize: return -1 # curid表示最后的状态的id值,count表示总的结点的数目, path表示变换的路径,evaluate_value表示每一个结点的评估值 return curid, count, path, evaluate_value
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 输出界面动态显示OPEN表的结点数、总扩展的结点数和评估函数最小的结点
示例如下: - 输出open表中在最佳路径上的结点与评估函数值并验证A算法所挑选出来的后继节点都必定满足: f(n)≤ f(S0)
以上的结果可以说明上面的条件了f(n)≤ f*(S0) - 验证h1(n)的单调性,显示凡A*算法挑选出来求后继的点ni扩展的一个子结点nj,检查是否满足: h(ni)≤ 1+h(nj)
- 如果将空格看作0,即九数码问题,利用相似的启发函数h1(n)和h2(n),求解相同的问题的搜索图是否相同?
- 求解相同的问题的搜索是不相同的, 因为在进行评估的时候会评估的结果是不一样的,因为前面默认为空的时候不会将其作为数字然后计入放错位置元素的个数以及没有放错的曼哈顿距离。而作为数字0的时候就会增加这一部分的数值。 而这就导致了搜索的空间是不一样的。 同时九数码问题还不符合A*条件。
如下:
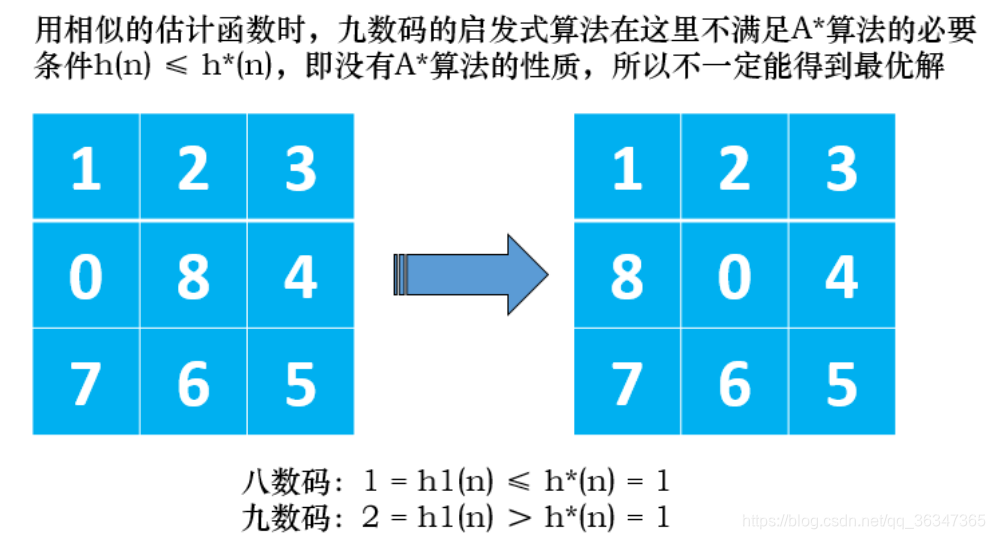
- 求解相同的问题的搜索是不相同的, 因为在进行评估的时候会评估的结果是不一样的,因为前面默认为空的时候不会将其作为数字然后计入放错位置元素的个数以及没有放错的曼哈顿距离。而作为数字0的时候就会增加这一部分的数值。 而这就导致了搜索的空间是不一样的。 同时九数码问题还不符合A*条件。
代码
链接: A*算法
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/你好赵伟/article/detail/786624
推荐阅读
相关标签



