点云地面滤波--渐进式形态学滤波_渐进形态滤波

1 形态学滤波简介

形态学滤波主要包括腐蚀和膨胀以及二者相结合产生的开、闭操作。
腐蚀：即去除不必要的部分，简化物体的形状。举个例子：一棵大树，去掉树叶，只保留树干，用树干表示树木，即提取树木的“骨架”，保留主要信息，表示原来的物体。可以去掉一些噪点，简化点云。
膨胀：即在物体原有的基础上，增加物体的体积。举个例子：一棵大树，使得树叶增加茂密，树干更加粗壮，在视觉上显得树木细节更加丰富，依次表示原来的物体。可以修复一些空洞使得细节更加饱满。
开操作：先腐蚀后膨胀的操作称之为开操作。它具有消除细小物体，在纤细处分离物体和平滑较大物体边界的作用，使得物体的骨架更加突出。
闭操作：先膨胀后腐蚀的操作称之为闭操作。它具有填充物体内细小空洞，连接邻近物体和平滑边界的作用，同样可以使得物体骨架更加突出。

2点云渐进式形态学滤波基本原理

窗口大小对于形态学地面滤波至关重要。因此形态学地面滤波重点讨论如何确定最优的窗口大小。对于这个问题可以通过逐渐增大形态学滤波器的窗口尺寸来解决，这种方法被称为渐进式形态学滤波。下图说明这种方法的过程：

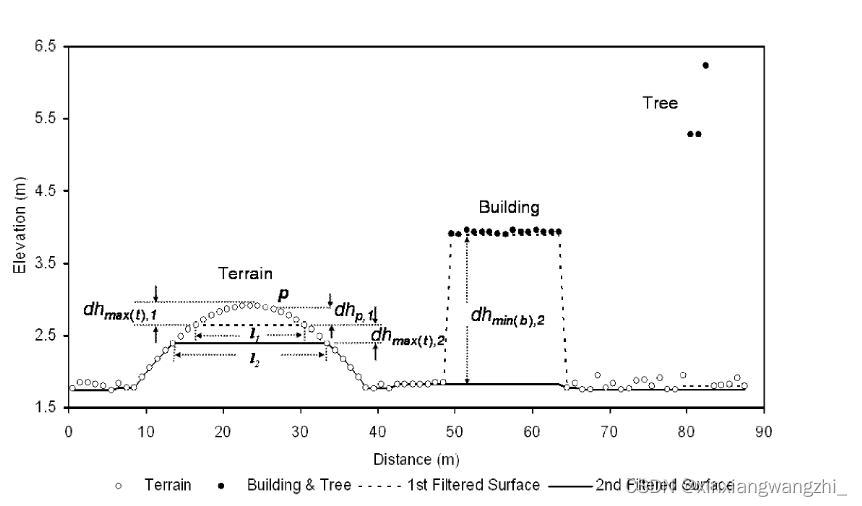
上图表示渐进式形态学滤波识别地形和建筑物量测的过程。这些点代表基于LIDAR采集的点云。第一个滤波高程面(虚线)是通过对原始点数据应用窗口大小为15 m 的开运算得到的。通过对第一个滤波曲面施加窗口大小为21 m的开运算得到第二个滤波高程曲面(实线)。
然而，在上图中的滤波过程往往会产生一个位于地形测量点云下方的表面，导致高处起伏地形顶部的测量点云被错误去除。即使在平坦的地面区域，过滤后的表面通常位于原始测量点云下方。因此，对于地形的大部分测量点云会被去除。这个问题可以通过引入基于地形、建筑物和树木的高度变化的高度差阈值来克服。下图说明了渐进式形态学滤波的主要过程：

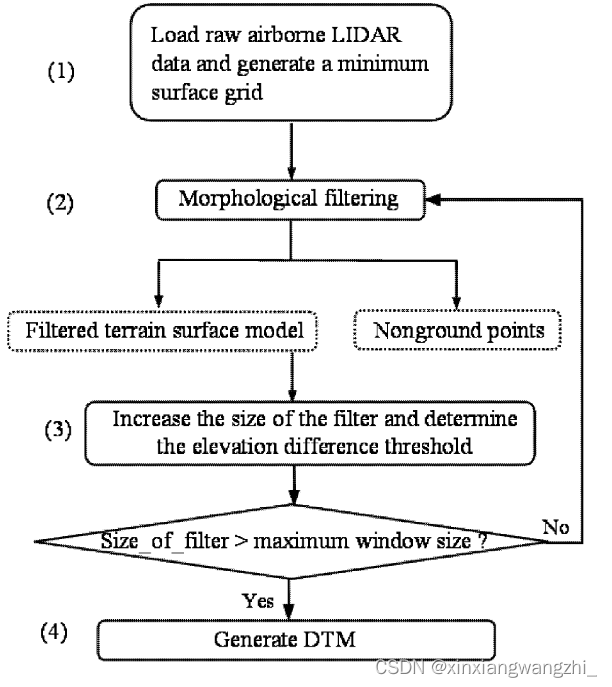
• 步骤1：加载激光雷达测量的点云坐标（x，y，z）。分为二维网格，在每个网格中选择最小高程点云，用这些点云构建最小表面网格。网格中的所有点坐标（x，y，z）存储在每个网格单元中。如果单元格不包含测量点云，则会为其指定最近距离点云。
• 步骤2：将渐进形态学开操作的滤波器应用于网格表面。在第一次迭代时，最小高程曲面和初始过滤窗口大小为过滤器做为输入（形态学滤波一共两个输入）。在接下来的迭代中，从上一次迭代中获得的过滤曲面和步骤3中增加的窗口大小被用作过滤器的输入。该步骤的输出包括：a）来自形态滤波器的进一步平滑曲面和：b）基于高程差阈值的检测到的非地面点。
• 步骤3：增加过滤器窗口的大小并计算高程差阈值。重复步骤2至3，直到过滤器窗口的大小大于预定义的最大值。此值通常设置为略大于最大建筑尺寸。
• 步骤4：最后一步是在删除非地面点云后，根据数据集生成DTM。

3参数设置

3.1窗口大小

在应用形态学滤波时，窗口大小和高差阈值的选取对取得良好的效果至关重要。对于窗口大小的选择，一个直观的选择是通过以下公式线性增加窗口大小$w_k$：
$$w_k=2kb+1\text{\hspace{1em}(1)}$$
$k$:迭代次数，$b$:初始窗口大小。然而，对于具有大型非地面物体的区域，需要相当长的计算时间。
或者也可以采用下面这种方法：
$$w_k=2b^k+1\text{\hspace{1em}(2)}$$

3.2高差阈值

高差阈值可根据研究区地形坡度确定。假设坡度不变，地形最大高差$d{h}_{\max (t),k}$、窗口大小$w_k$与地形坡度$s$之间存在关系：
$$s=\frac{d{h}_{\max (t),k}}{\frac{\left(w_k-w_{k-1}\right)}{2}}\text{\hspace{1em}(3)}$$
高差阈值$d{h}_{T,k}$:
d h T , k = { d h 0 ,  if  w k ≤ 3 s ( w k − w k − 1 ) c + d h 0 ,  if  w k > 3 d h max ⁡ ,  if  d h T , k > d h max ⁡ (4) d h_{T, k}=

$$\begin{cases}d h_0, & \text { if } w_k \leq 3 \\ s\left(w_k-w_{k-1}\right) c+d h_0, & \text { if } w_k>3 \\ d h_{\max }, & \text { if } d h_{T, k}>d h_{\max }\end{cases}$$ \tag{4} dhT,k​=⎩ ⎨ ⎧​dh0​,s(wk​−wk−1​)c+dh0​,dhmax​,​ if wk​≤3 if wk​>3 if dhT,k​>dhmax​​(4)
$d{h}_0$:初始高差阈值，$s$:坡度，$c$:网格尺寸，$d{h}_{max}$:最大高差阈值,$k$:迭代次数。
在城市地区，主要的非地面物体包括汽车、树木和建筑物。单个汽车和树木的尺寸远小于建筑物的尺寸，因此大多数汽车和树木通常在前几次迭代中被移除，而大型建筑物将在最后被移除。最大高差阈值可以设置为固定高度（例如，最低建筑高度），以确保识别建筑群。通常通过反复比较过滤和未过滤的数据来达到最佳效果。另一方面，山区的非地面物体主要是植被（树木）。不需要设置固定的最大高差阈值来移除树木，通常将其设置为研究区域内最大的高差。

4算法流程

4.1输入：

• 原始点云
• 网格尺寸
• 初始窗口大小$b$
• 最大窗口尺寸$max-window-size$
• 坡度$s$
• 初始高差阈值$d{h}_0$
• 最大高差阈值$d{h}_{max}$

4.2输出：

• 地面点与非地面点

4.3算法流程：

1.计算$x,y$最大值最小值
2.划分$m\ast n$二维网格： $m=$ floor $[(\max (y)-\min (y))/c]+1$ and $n=$ floor $[(\max (x)-\min (x))/c]+1$
3.将点云坐标放进二维数组$A[m,n]$（二维数组表示网格）中。遍历每个点，根据其x和y坐标，确定该点落在哪个网格中。如果同一网格单元中有多个点，选择高程最小的点。
4.使用最近邻法插值A中不包含任何点的网格。将这些插值网格的x和y坐标设置为零，以将它们与包含激光雷达点的网格单元区分开来。将A复制到B。用0初始化二维数组的元素。
5.用公式（1）或（2）计算$w_k$，$w_k<max-window-size$
6.$d{h}_T=d{h}_0$
07. for each window size $w_k$
08. \quad for $i=1$ to $m$
09. \quad\quad $P_i=A[i;](A[i;]$ represents a row of points at row $i$ in $A$ and $P_i$ is a $1-$ D array)
10. \quad\quad $Z\leftarrow Pi$ (Assign elevation values from $P_i$ to a 1-D elevation array $Z$ )
11. \quad\quad $Z_f=\mathrm{erosion}\left(Z,w_k\right)$
12. \quad\quad $Z_f=\mathrm{dilation}\left(Z_f,w_k\right)$
13. \quad\quad $P_i\leftarrow Z_f$ (Replace $z$ values of $P_i$ with the values from $Z_f)$
14. \quad\quad $A[i;]=P_i$ (Put the filtered row of points $P_i$
back to row $i$ of array $A$ )
15. \quad\quad for $j=1$ to $n$
16. \quad \quad\quad\quad if $Z[j]-Z_f[j]>d{h}_T$ then flag $[i,j]=w_k$
17. \quad\quad end for $j$ loop
18. \quad end for $i$ loop
19. \quad if $\left(d{h}_T>d{h}_{\max }\right)$
20. \quad $d{h}_T=d{h}_{\max }$
21. \quad else
22. \quad $d{h}_T=s\left(w_k-w_{k-1}\right)c+d{h}_0$
23. end for window size loop
24. for $i=1$ to $m$
25. \quad for $j=1$ to $n$
26. \quad \quad if $(B[i,j](x)>0$ and $B[i,j](y)>0)$
27. \quad \quad \quad if $($ flag $[i,j]=0)$
28. \quad \quad \quad \quad $B[i,j]$ is a ground point
29. \quad \quad \quad else
30. \quad \quad \quad \quad $B[i,j]$ is a nonground point
31. \quad end for $j$ loop
32. end for $i$ loop
$\underline{\mathrm{Erosion}\left(Z,w_k\right)}$ :

1. for $j=1$ to $n$
2. $Z_f[j]={\min }_{j-\left[w_k/2\right]\le l\le j+\left[w_k/2\right]}(Z[l])$
3. return $Z_f$

Dilation $\left(Z,w_k\right)$ :

1. for $j=1$ to $n$
2. $Z_f[j]={\max }_{j-\left[w_k/2\right]\le l\le j+\left[w_k/2\right]}(Z[l])$
3. return $Z_f$

5渐进式形态学滤波在PCL应用：

#include <iostream>
#include <pcl/io/pcd_io.h>
#include <pcl/point_types.h>
#include <pcl/filters/extract_indices.h>
#include <pcl/segmentation/progressive_morphological_filter.h>

int main()
{
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_filtered(new pcl::PointCloud<pcl::PointXYZ>);
	pcl::PointIndicesPtr ground(new pcl::PointIndices);

	pcl::io::loadPCDFile<pcl::PointXYZ>("SHCSCloud副本.pcd", *cloud);

	std::cout << "Cloud before filtering: " << std::endl;
	std::cout << cloud->points.size() << std::endl;

	// Create the filtering object
	pcl::ProgressiveMorphologicalFilter<pcl::PointXYZ> pmf;
	pmf.setInputCloud(cloud);
	pmf.setCellSize(2.0);
	pmf.setBase(1.0);
	pmf.setMaxWindowSize(5);
	pmf.setSlope(1.0f);
	pmf.setInitialDistance(0.5f);
	pmf.setMaxDistance(5.0f);
	pmf.extract(ground->indices);

	// Create the filtering object
	pcl::ExtractIndices<pcl::PointXYZ> extract;
	extract.setInputCloud(cloud);
	extract.setIndices(ground);
	extract.filter(*cloud_filtered);

	std::cout << "Ground cloud after filtering: " << std::endl;
	std::cout <<   cloud_filtered->points.size() << std::endl;

	pcl::io::savePCDFile <pcl::PointXYZ>("ground.pcd", *cloud_filtered, false);

	// Extract non-ground returns
	extract.setNegative(true);
	extract.filter(*cloud_filtered);

	std::cout << "Object cloud after filtering: " << std::endl;
	std::cout << cloud_filtered->points.size() << std::endl;

	pcl::io::savePCDFile("object.pcd", *cloud_filtered, false);

	return (0);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

过滤效果：

参考

形态学简介
pcl
《A progressive morphological filter for removing nonground measurements from airborne LIDAR data》