C语言|深入浅出讲解int转换为float全过程(附2017年统考大题案例)_int转float

目录

0.前言

1.浮点数存储规则(以float为例)

2.用案例讲解float从真值到存储的过程

a) 案例

b)问题出现

c).问题分析

 i). 真值计算

 ii). int和float存储

3.int转换float的过程

---

0.前言

最近在学习王道计组的第二章，数据的表示和运算。当学到C语言中int和float类型转换的时候，我便有个问题，为什么int到float会有精度损失？是因为int的有效数值为是31位，而float的有效位是24位(1+23,1被隐藏)，网上也没有这个详细的解答(知道float如何存储，但是还是不懂为何精度损失...)。当做了2017年的浮点数统考大题(这个大题出的真是好)，我便彻底搞懂了float的存储规则及舍弃。本文就以int转为float的例子，解析精度损失的详细过程。

1.浮点数存储规则(以float为例)

关于浮点数如何存储，分为阶符，阶码，尾数的三个部分，网上和辅导书有很详细的说明，这里我就不过多解释了，如有不懂，看下面大佬的博客。一定要理解浮点数存储规则，再理解下文。

(82条消息) 浮点数的存储规则【带案列讲解，轻松理解浮点数的存储规则】_浮点的规则__featherbrain的博客-CSDN博客

 

2.用案例讲解float从真值到存储的过程

a) 案例

案例代码来自2017年统考大题，下面代码的目的是为了计算 (总之,用二进制看，就是计算n+1位全1的和)，试问，f(0) ~ f(31)中f1和f2的结果都相等吗？

//f1是用int类型存储结果
int f1(unsigned n)
{
	int sum = 1;
	int pow = 1;
	for (unsigned i = 0; i <n; i++)
	{
		pow *= 2;
		sum += pow;
	}
	return sum;
}
 
//f2是用float类型存储结果
float f2(unsigned n)
{
	float sum = 1;
	float pow = 1;
	for (unsigned i = 0; i < n; i++)
	{
		pow *= 2;
		sum += pow;
	}
	return sum;
}
 
//比较f1和f2的运行结果
int main()
{
	for (int i = 0; i < 32; i++)
	{
		printf("%d\t%-20d %.1f\n",i ,f1(i), f2(i));
	}
    return 0;
}

b)问题出现

当跑了上面的代码后，我们发现，自f(24)后，f1和f2结果开始不相等。而且f1的结果是准确的(除f1(31)发生了溢出，这个好理解），而f2结果总是大了1，这是为什么呢?

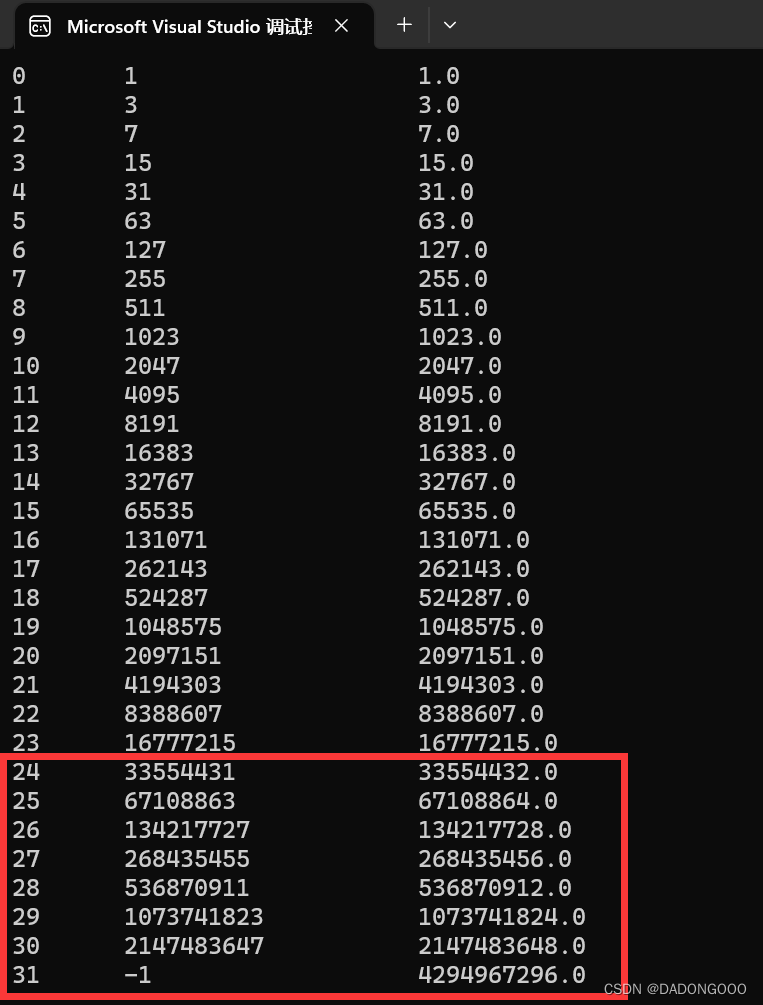
c).问题分析

C语言中，float类型的存储是按照 计算真值 -> 存储数据 过程进行的。我们首先分析函数真值大小。 

 i). 真值计算

这里出现异常的是f(24)，但是前一个f(23)并没有出现异常，这里我们拿这两个来分析。

如果要存储浮点数，按照IEEE754标准，结果得化成 

  

如果用int和浮点数能够表示，则真值的结果应该是如上图，float存储的方式也应该如上图所示 

 ii). int和float存储

int的范围没有超出，很容易判断，而float的存储是1位数符 + 8位阶码 + 23位尾码，我们可以很明显的看到，f(23)的最低位数是2^-23,而f(24)的最低位数是2^-24，因为float只有23位尾码，所以f(23)可以正常存储，而f(24)需要舍弃2^-24，因此便出现了精度损失。

C语言的舍入规则是，舍1进1，舍0进0，因此f(24)因为舍去了2^-24，因此要向高位进1，结果便比f1(24)大1。

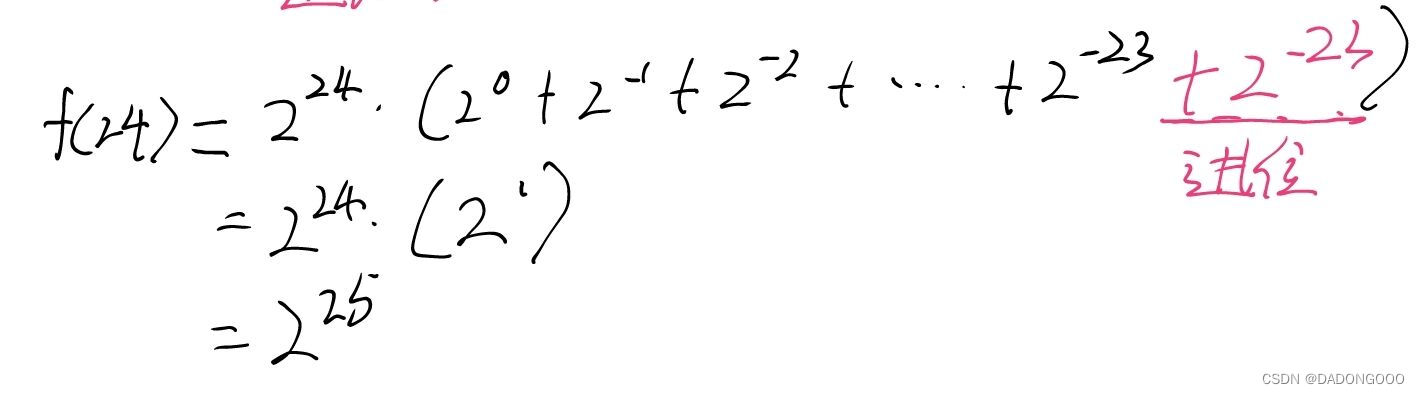
 因此，这就是为什么f(24)之后f2与f1不等，且f2总比f1大1(i = 31除外)。因为精度发生了损失，要进行舍入操作，按照舍1进1，舍0进0的规则，因此f2比f1大了1。

（这里建议浮点数的表示可以按照上述用2^n来表示，不建议用(1.00111)B，该方法麻烦，且没有上面明了。看自己习惯)

3.int转换float的过程

看懂了上面，聪明的你一定能够明白int转换为float。为什么可能会发生精度损失，一样是按照上面的方法，写出真值表达式，再分析float的存储。

C语言中，int到float类型转换的过程是，计算真值 -> 按照float规则存储，int到float类型的强制转换过程分析和上面过程一样，当数值位不够时，便发生了精度损失。

相信你，看懂了这一篇文章，对int转换为float和float的精度损失有了有了更深的理解。如果能够帮你弄懂这个问题，这便是我的初衷。