【数据结构的排序算法1】插入排序与希尔排序详解_插入排序和希尔排序

1. 排序的概念及其运用

1.1 排序的概念

排序： 所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
稳定性： 假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r [ i ] = r [ j ]，且 r [ i ] 在 r [ j ] 之前，而在排序后的序列中，r [ i ] 仍在 r [ j ] 之前，则称这种排序算法是稳定的；否则称为不稳定的。
内部排序： 数据元素全部放在内存中的排序。
外部排序： 数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

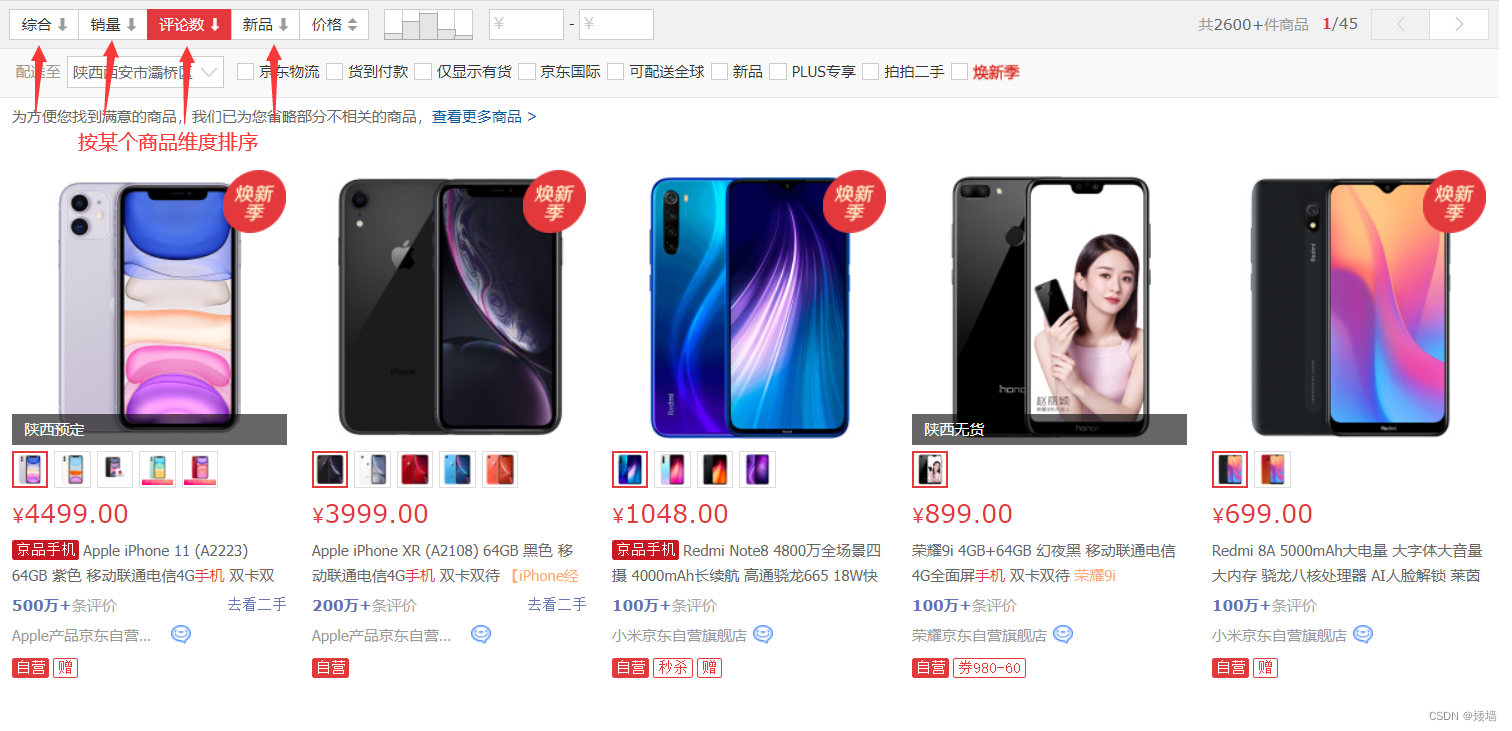
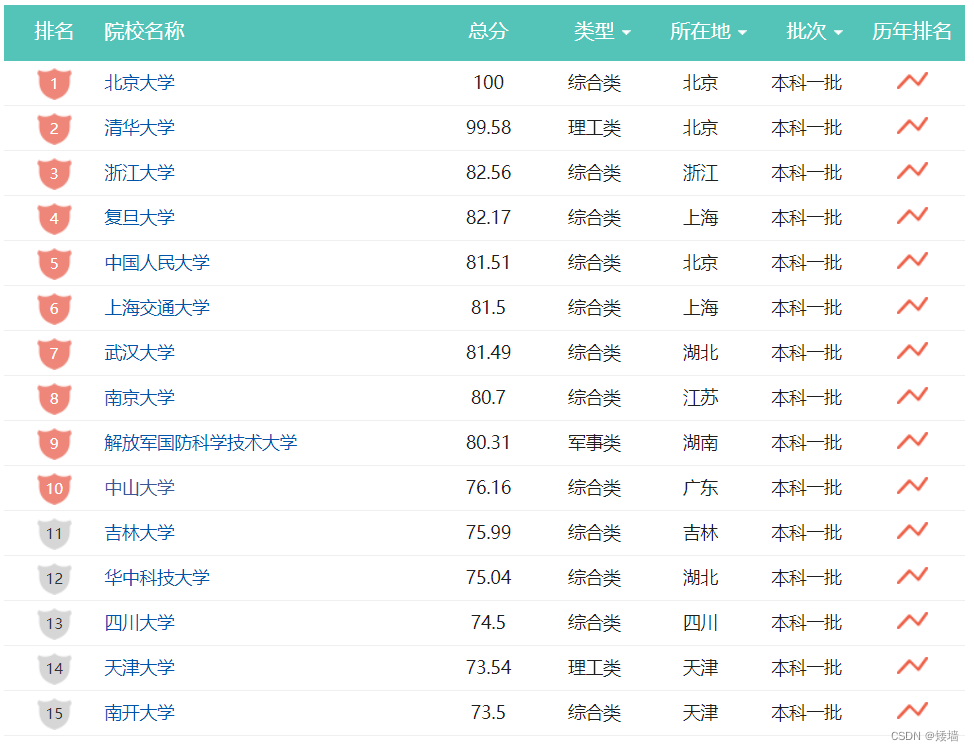
1.2 排序的运用

排序有很多应用场景，以下为应用场景举例。

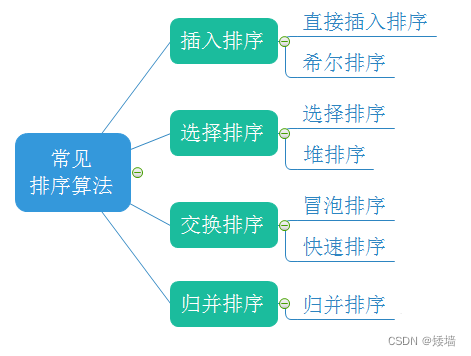
1.3 常见的排序算法

常见的排序算法有以下几种，今天主要介绍的排序算法是插入排序和希尔排序。

2 插入排序

2.1 基本思想

插入排序算法的基本思想是把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列。
实际中生活中，我们玩扑克的时候，就用了插入排序的思想。

2.2 动态图示

当插入第 i (i >= 1) 个元素时，前面的 i - 1 个元素已经排好序了，此时将 i 个元素依次从后向前和前面的元素相比。如果前面的元素大于第 i 个元素，则原来位置上的元素往后移动一位。如果前面的元素小于第i个元素，则第 i 个元素插入到前面元素的后面。

2.3 简单举例

简单举例：
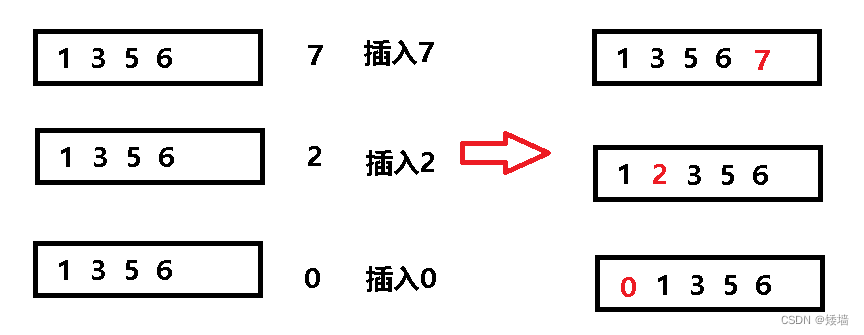
假设向有序数列 1、3、5、6 分别插入7、2 和 0，那么它们插入的位置是不同的，结果如图所示：


如果插入的数据比 end 位置的数据大，就放到 end 的后一个位置



如果插入的数据比 end 位置的数据小，就挪动并且 –end



如果插入的数据比第 0 个位置的数据都小，end就指向 -1 位置

2.4 代码解析

插入一个值的情况：

首先先写出插入一个值的情况，定义 end 为最后一个数据的位置，将需要插入的数据保存在一个变量中，然后根据上面分析的情况进行判断，如果最后一个位置的值大于插入的值，就挪动数据，并且 –end，如果最后一个位置的值小于要插入的值，就退出 while 循环，将数据直接插入到 end 后。

注意：

如果插入的数据比所有数都小，最后一次进入 while 循环，–end 后 end 为 -1，此时退出 while 循环，而需要在循环外面将 tmp 放入 a[end+1] 位置，才能保证成功插入数据。

		//单趟
		int end;
		//将插入的数据保存起来
		int tmp = a[end + 1];
		//判断结束条件，end>=0就继续，当插入的数据比所有值都小，edn比0小时就结束
		while (end >= 0)
		{
			//如果插入的值比end位置的值小，end位置的值往后挪
			if (tmp < a[end])
			{
				a[end + 1] = a[end];
				--end;
			}
			//如果插入的值比end位置的值大，就放到end位置的后一个位置
			//这里不写a[end+1] = tmp,而是直接退出while循环
			//因为如果插入的数据比所有值都小，while循环就退出去了，无法将其放到数据第一个位置
			else
			{
				break;
			}
		}
		a[end+1] = tmp;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

以上只是介绍了单次插入的情况，而怎么利用插入排序的思想对整个数组进行排序呢？

第一次认为第一个数是有序的，将第二个数插入进来，然后前两个数有序了，再将第三个数插入进来，前 n-1 个数据有序，将第 n 个数据插入进来，所以只需要通过一个循环控制 end 的位置。



代码如下，注意循环里的的结束条件是 i < n - 1 ，因为如果是 i < n 最后 end 落的位置就是 n - 1，此时 tmp 是 end + 1 的位置，造成越界现象，所以结束条件应该为i < n - 1，最后 end 落的位置是 n - 2，此时插入最后一个数据才正确。

代码如下：

// 插入排序
//插入排序是向已经有序的序列中插入新的数据，保证插入后的整个数据保持有序
void InsertSort(int* a, int n)
{
	//这里i应该小于n-1，因为要排一个数组，n是数据个数，如果i<n，最后一次循环是end = n-1，a[end+1]就会越界
	for (int i = 0; i < n-1; ++i)
	{
		//这里是单趟排序，只保证了前面数组有序的基础上插入新的数据后，新的数组仍为有序
		
		//单趟排，让end = i
		int end = i;
		//将插入的数据保存起来
		int tmp = a[end + 1];
		//判断结束条件，end>=0就继续，当插入的数据比所有值都小，edn比0小时就结束
		while (end >= 0)
		{
			//如果插入的值比end位置的值小，end位置的值往后挪
			if (tmp < a[end])
			{
				a[end + 1] = a[end];
				--end;
			}
			//如果插入的值比end位置的值大，就放到end位置的后一个位置
			//这里不写a[end+1] = tmp,而是直接退出while循环
			//因为如果插入的数据比所有值都小，while循环就退出去了，无法将其放到数据第一个位置
			else
			{
				break;
			}
		}
		//插入位置的值比end位置的值大，就将其放入end+1位置
		//当插入数据比所有值都小，说明while循环结束，此时end = -1，需要将tmp值放到第0个位置，所以
		a[end + 1] = tmp;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

2.5 插入排序的时间复杂度分析

时间复杂度： O(N^2)
最坏的情况： 逆序的情况是最坏的情况，比如如果排升序，而给定的序列是降序，则每次进行插入的时候都需要将新插入的数据挪动到最前面，第一次插入挪动1次，第二次插入挪动2次，以此类推最后挪动了等差数列求和次，量级为N^2。
最好的情况： 顺序有序或者接近顺序有序，每个数据插入进入都退出 while 循环直接插入到 end 的后一个位置，所以时间复杂度为O(N)。

3 希尔排序

1、当插入排序为逆序的情况，针对插入排序逆序时间复杂度为 N^2 的问题，提出希尔排序，希尔排序法又称缩小增量法。

2、希尔排序法的基本思想是：先进行预排序然后再插入排序。

3、先选定一个整数 gap，把待排序的数组分成个 gap 组，每组有 n / gap 个元素，所有距离为 gap 的元素分在同一组内，并对每一组内的元素进行排序。然后缩小 gap 的值，去重复上述分组和排序的工作。当 gap == 1 时，数组就达到了有序。

3.1 预排序

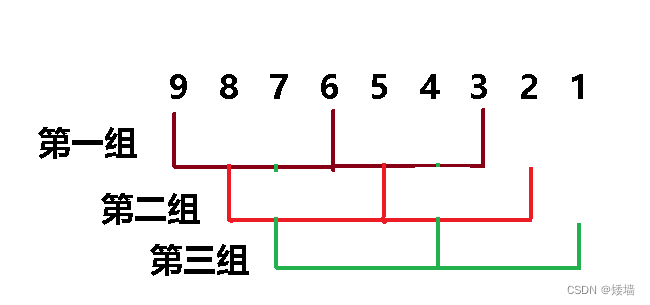
当需要排序的序列为逆序时，挪动数据的次数较多，所以可以将数据进行分组排序，以升序为例，让值大的数据尽快跳到后面，而让值小的数据尽快跳到前面。以下面的数据为例，取 gap 为 3，就是间距为 3 的数据为一组，这些数据就被划分成以下几组。


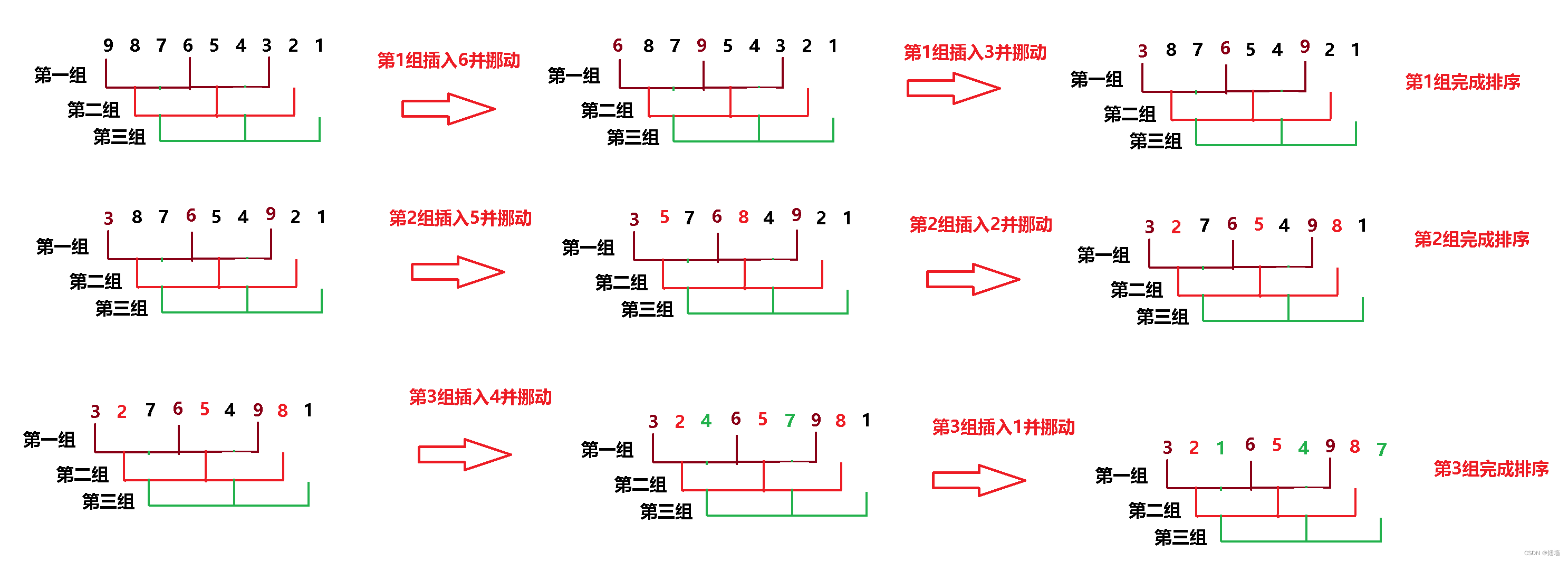
将每一组进行预排序，如下图所示：



先实现间距为 gap 的插入排序，也就是实现上面其中一组的排序代码。

1、gap为 3，我们将 end 的后一个位置插入进去，此时间距为 gap，所以 end 的后一个位置为 end + gap，将其存入到变量 tmp 中

2、 while 循环结束的条件没有变，仍为 end >= 0，如果插入的值比 end 位置的值小，就挪动数据，注意此时不是挪动一位数据，而是挪动 gap 位数据

3、同时 end 变为它的前一个位置，所以时 end -= gap。

4、当插入的数据比当前组所有数据都小的时候，end 最后变成了 -gap，此时将数据放到当前组的第 0 个位置，所以最后是 a[end+gap] = tmp。



这里思想和直接插入排序很像，因为如果将 gap 取 1，就是直接插入排序，将一组数据排完需要控制 end 的位置，因为直接插入排序 for 循环的终止条件是 n-1，而这里的间距是 gap，所以此时这里的 for 循环终止条件位 n-gap，然后 i 每次变化 gap 个位置。

代码如下：

for (int i = 0; i < n - gap; i += gap)
		{
			int end = i;
			//end的后一个位置的数据是a[end+gap]
			int tmp = a[end + gap];
			while (end >= 0)
			{
				//如果插入的值比end位置的值小，end位置的值往后挪gap个位置，同时end要减gap个位置
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				//如果插入的值比end位置的值大，就放到end位置的后一个位置
				//这里不写a[end+1] = tmp,而是直接退出while循环
				//因为如果插入的数据比所有值都小，while循环就退出去了，无法将其放到数据第一个位置
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

3.2 总实现

当前只完成了一组的排序，怎么走完 gap 组呢？

只需再嵌套一层 for 循环，当 j 为 0 ，走的第一组，当 j 为 1 走的第二组，当 j 为 2 走的是第三组。代码如下：

// 希尔排序
// 针对插入排序逆序时间复杂度为 N^2 的问题，提出希尔排序
// 思想是先进行预排序，再进行插入排序 
// 预排序是将其分为gap组，将每组数据进行插入排序
void ShellSort(int* a, int n)
{
	//首先实现一个间距为gap的插入排序
	int gap = 3;
	for (int j = 0; j < gap; ++j)
	{
		for (int i = 0; i < n - gap; i += gap)
		{
			int end = i;
			//end的后一个位置的数据是a[end+gap]
			int tmp = a[end + gap];
			while (end >= 0)
			{
				//如果插入的值比end位置的值小，end位置的值往后挪gap个位置，同时end要减gap个位置
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				//如果插入的值比end位置的值大，就放到end位置的后一个位置
				//这里不写a[end+1] = tmp,而是直接退出while循环
				//因为如果插入的数据比所有值都小，while循环就退出去了，无法将其放到数据第一个位置
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

还有一种简化写法，就是 gap 组并排，代码如下：

void ShellSort(int* a, int n)
{
		//gap组并排
		int gap = 3;
		for (int i = 0; i < n - gap; ++i)
		{
			int end = i;
			//end的后一个位置的数据是a[end+gap]
			int tmp = a[end + gap];
			while (end >= 0)
			{
				//如果插入的值比end位置的值小，end位置的值往后挪gap个位置，同时end要减gap个位置
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				//如果插入的值比end位置的值大，就放到end位置的后一个位置
				//这里不写a[end+1] = tmp,而是直接退出while循环
				//因为如果插入的数据比所有值都小，while循环就退出去了，无法将其放到数据第一个位置
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

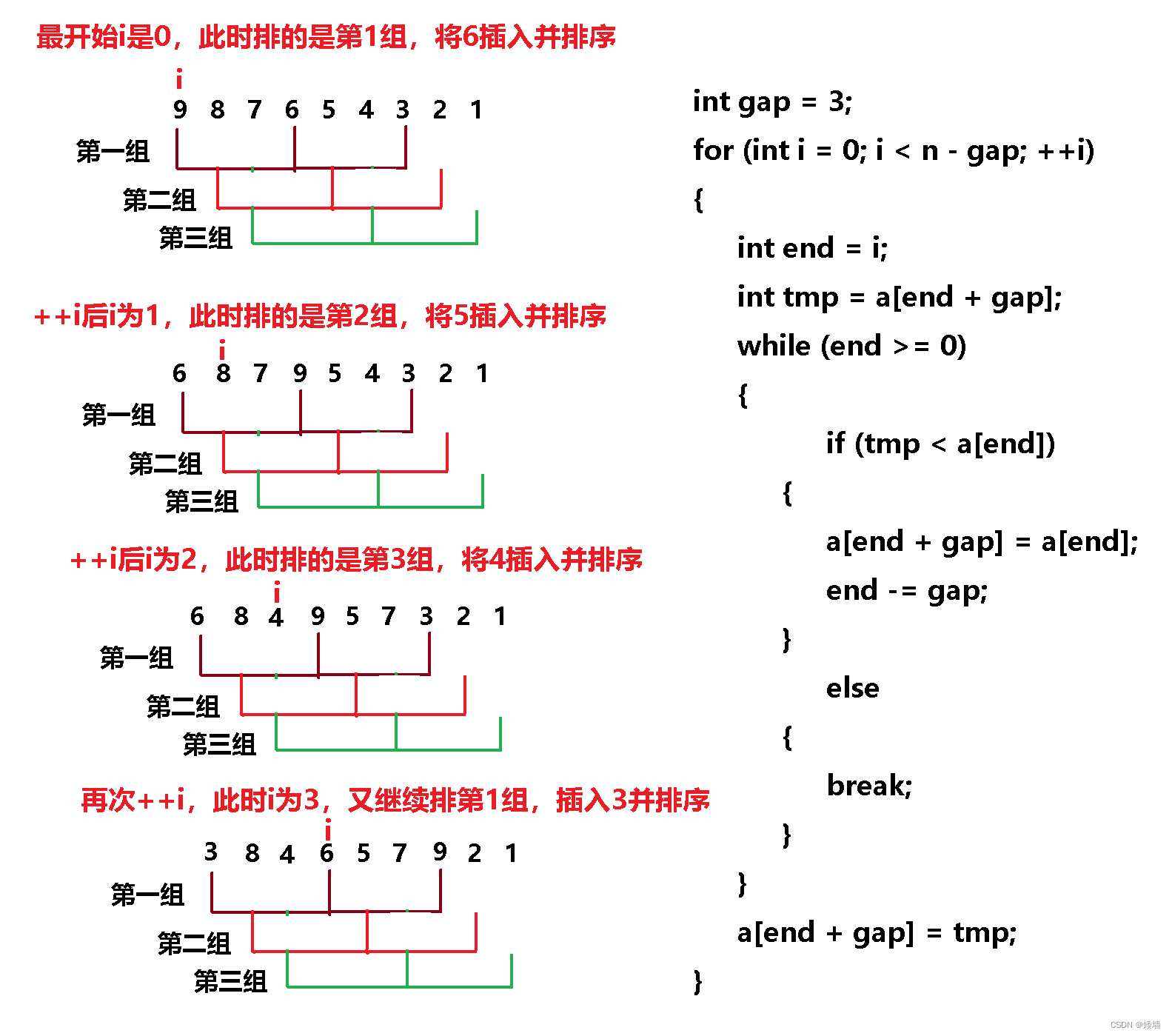
代码分析如下图所示：



最后考虑一个问题：gap 为多少更合适呢？

1、因预排序可以进行很多次，只需要保证预排序完成后，最后一次是插入排序即可，所以此时先让 gap 为 n，用 while 循环判断 gap 是否为1

2、gap 为 1 就进行插入排序

3、如果 gap 不是 1 ，就让 gap = gap/2，并继续进行预排序。

4、最后一次进入 while 循环，gap/2 肯定为 1，此时进行的就是插入排序。

5、也可以让 gap = gap/3+1，规则是保证最后一次是插入排序即可。

代码如下：

void ShellSort(int* a, int n)
{
	//首先实现一个间距为gap的插入排序
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		for (int i = 0; i < n - gap; ++i)
		{
			int end = i;
			//end的后一个位置的数据是a[end+gap]
			int tmp = a[end + gap];
			while (end >= 0)
			{
				//如果插入的值比end位置的值小，end位置的值往后挪gap个位置，同时end要减gap个位置
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				//如果插入的值比end位置的值大，就放到end位置的后一个位置
				//这里不写a[end+1] = tmp,而是直接退出while循环
				//因为如果插入的数据比所有值都小，while循环就退出去了，无法将其放到数据第一个位置
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

3.3 时间复杂度分析

最坏的情况： 最外面的循环有 gap 次，里面的循环，每一组有 n/gap 个数据，每组最坏的情况挪动 1+2+3+…+n/gap 次。所以总的挪动次数为 (1+2+3+…+n/gap-1) * gap 。所以此时时间复杂度为 O(N^2)。

最好的情况： 已经是有序，就是O(N)。

参考资料：

1、《数据结构(C语言版)》— 严蔚敏




2、《数据结构-用面相对象方法与C++描述》— 殷人昆



总结：

1、当 gap > 1 时都是预排序，目的是让数组更接近于有序。当 gap == 1 时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。

2、希尔排序的时间复杂度不好计算，因为 gap 的取值方法很多，导致很难去计算，因此在好些书中给出的希尔排序的时间复杂度都不固定。我们通常认为希尔排序的时间复杂度为 O(N^1.3)。

4 插入排序和希尔排序性能对比

首先写一个测试函数，用于测试各种排序算法的性能，代码如下：

//性能测试函数
void TestOP()
{
	//产生随机数
	srand(time(0));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	if (a1 == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	int* a2 = (int*)malloc(sizeof(int) * N);
	if (a2 == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	
	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
		a2[i] = a1[i];
	}
	//程序获取调用函数的执行时间，两个函数的执行时间相减就是程序执行的时间
	int begin1 = clock();
	InsertSort(a1, N);
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	printf("InsertSort:%d\n", end1 - begin1);
	printf("ShellSort:%d\n", end2 - begin2);
	
	free(a1);
	free(a2);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

执行结果如下，可以观察到希尔排序比插入排序性能查了接近一百倍。


注意测试性能的时候要换到 release 版本进行测试