中心极限与大数定理律的关系_拓扑动力系统(3): 射影极限自然扩充, 拓扑传递性...

内容提要:

1 拓扑知识回顾; 2 射影极限自然扩充; 3 拓扑传递性; 4 点传递系统; 本文主要参考文献.

本文的前置内容为:

格罗卜学数学：拓扑动力系统(1): 基本概念, Li-Yorke定理和Sharkovskii定理

格罗卜学数学：拓扑动力系统(2): 极小集, Birkhoff定理, ω极限点

本文之后请继续食用:

格罗卜学数学：拓扑动力系统(4): 拓扑熵

更多内容，请移步专栏目录:

格罗卜：格罗卜的数学乐园-目录​zhuanlan.zhihu.com

设

紧致Hausdorff空间, 连续映射, 紧致拓扑离散半动力系统, 简称 紧致系统,记为

1 拓扑知识回顾

以下的结论都是基础的.

1-1. Hausdorff性质(

任意可乘的, 遗传的.

1-2. 第二可数性质(

可数可乘的, 遗传的.

1-3. 紧致性是任意可乘的, 闭遗传的.

1-4.

有限可乘的. 闭遗传的.

• 在可乘性表现不好, 紧致性有助于改善它的可乘性.

1-5. 拓扑空间

1-6. [度量化定理] 拓扑空间

1-7. 度量空间的完备性是可数可乘的, 闭遗传的.

1-8. [我们需要的结果] 一系列 紧致, Hausdorff, 第二可数 的拓扑空间的可数乘积依然是紧致, Hausdorff, 第二可数的拓扑空间, 它是可度量化的. 并且如果这一系列空间是完备的, 乘积空间依然是完备的.

可以参考如下的表格^[1]:

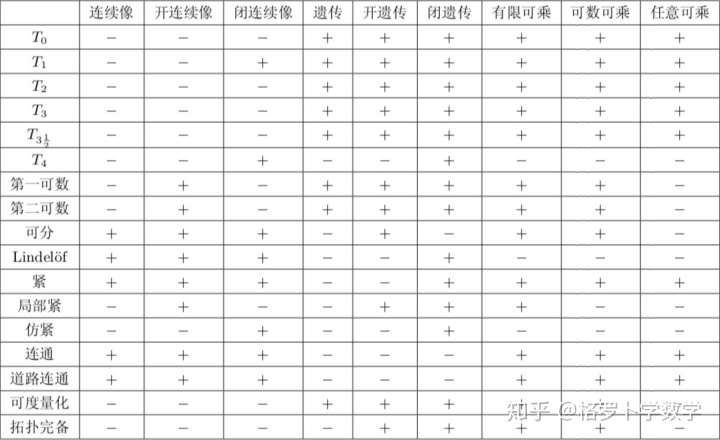
2 射影极限自然扩充

2-1. 设

紧致Hausdorff空间, 满(!)映射.

考虑如下的逆向系统:

并取射影极限

设

由上一节对拓扑性质的讨论, 这依然是紧致Hausdorff空间.

2-2. [自然扩充动力系统] 在

容易看出

同胚!

把系统

自然扩充. 它把一个紧致拓扑离散 半动力系统变成了 动力系统.

3 拓扑传递性

3-1. [拓扑传递系统] 紧致系统

拓扑传递的, 如果对任意非空开集

3-2. [传递系统的等价描述] 下述诸条件是等价的:

• (a)
  是拓扑传递的;
• (b) 若
  是非空开集, 那么
  稠密;
• (c) 若
  是非空开集且
  , 则
  在
  中稠密;
• (d) 若
  为闭不变的, 则
  或
  为无处稠密的. [称
  是
  无处稠密的, 如果
  的闭包的内部是空集]

[证明] (a)

(b). 显然.

(b)

(c). 若

是非空开集且

, 则

在

中稠密;

(c)

(d). 设

, 则

是开集且

, 那么

或者

在

中稠密, 等价地,

或

为无处稠密的;

(d)

(a). 如果

是非空开集, 那么令

, 于是

为无处稠密的. 于是

稠密, 从而

.

3-3. [注记] 考虑和(1)相似的条件:

• (e) 对任意非空开集
  , 存在
  ,使得
  .
• (f) 对任意非空开集
  , 存在
  ,使得
  .

- 如果

[证明]

.

- 如果

3-4. 设

紧致Hausdorff空间, 满(!)映射.

• (1)
  满足(a) 当且仅当
  满足(a).
• (2)
  满足(e) 当且仅当
  满足(f).

3-5. [例子] 设

[解答] 假如

是

的开子集, 那么存在这样的

与

, 使得

. 由于

, 也就是说紧致系统

是传递的.

4 点传递系统

上面给出的拓扑传递性比较抽象, 不太易于理解, 和它相关联的是点传递的概念.

4-1. [点传递系统] 紧致系统

点传递的, 如果存在

4-2. [点传递系统和拓扑传递系统的关系]

设

• (1)
  是拓扑传递的;
• (2)
  是点传递的;
• (3) 集合
  是
  的一个处处稠密的
  型集. [回忆拓扑学的一个概念:
  的一个子集合叫做
  型集, 如果它是可数个开集的交集.]

本文主要参考文献:

周作领//尹建东//许绍元: 拓扑动力系统, 出版社:科学出版社, ISBN:9787030325860

拓扑动力系统 (豆瓣)​book.douban.com

叶向东/黄文/邵松: 拓扑动力系统概论, 出版社:科学出版社, ISBN:9787030205698

拓扑动力系统概论 (豆瓣)​book.douban.com

参考

1. ^张德学, 一般拓扑学基础讲义