- 1Big Model Weekly | 第29期
- 2华为OD面试手撕代码最新:最大子数组和_面试 最大数组和
- 3安卓设备如何ROOT?玩转ROOT,安装magisk,让你的安卓手机更强更好用_magisk root
- 4本地上传文件到FastDFS命令上传报错:ERROR - file connection_pool_fastdfs fastfilestorageclient上传文件报错
- 5内网前期准备小结(1),阿里一线架构师技术图谱
- 6模型微调实战:文本生成任务_文本生成模型微调
- 7文心智能体【焦虑粉碎机】——帮你赶走“坏”情绪_智能体的指令设置
- 8[flink]随笔
- 9【软件工具】如何使用 Jenkins 构建并部署一个 WAR 包到相应的服务器上
- 10geometry:MySQL的空间数据类型(Spatial Data Type)与JTS(OSGeo)类型之间的序列化和反序列化_mysql 空间数据库 geometry
机器学习基础——模型选择和评估_模型估计中数据选取与转换的依据是什么
赞
踩
一、归纳偏好
概念
归纳偏好指机器学习算法在学习过程中对某种类型假设的偏好。
假
设
−
>
{
尽
可
能
一
般
适用情况尽可能多
尽
可
能
特
殊
适用情况尽可能少
假设->
例如:若数据包含噪声,则假设空间中有可能不存在与所有训练样本都一致的假设。在这种情况下,通常认为两个数据的属性越相近,则更倾向于将它们划为同一类。对于出现相同属性却不同类的情况,可以认为是它属于与之最近邻的数据的属性类别;或者直接删除,但会丢失部分数据。这就是一种归纳偏好用于假设选择的例子。
重要性
任何一个有效的机器学习算法必有其归纳偏好,否则它将被假设空间中看似在训练集上”等效“的假设所迷惑,而无法产生确定的学习结果。
例:若认为相似样本应有相似的输出,结果可能是平滑的曲线。
确立正确的偏好的原则
- 奥卡姆剃刀(Occam’s razor):若有多个假设与观察一致,则选最简单的那个。
- 根据算法性能:好的归纳偏好对应学习算法所作出的关于”什么样的模型更好“的假设。在实际运用中,这个假设是否成立(即,归纳偏好是否与问题匹配)大多数直接决定了算法能否取得更好的性能。
没有免费的午餐定理
没有免费的午餐定理 (No Free Lunch Theorem , NFL定理):在没有实际背景下,没有一种算法比随机猜想的算法效果更好。
NFL定理的重要意义:在脱离实际情况下,空泛地谈论哪种算法好坏是毫无意义的,要谈论其优劣必须针对具体的学习问题。
二、模型选择
模型选择遇到的困难
模型选择的理想方案是:对候选模型的泛化误差进行评估,然后选择泛化误差最小的那个模型。
实际上,我们无法直接获得泛化误差,而训练误差又由于过拟合现象的存在就不适合作为标准。
解决方案:使用测试误差近似泛化误差。(实际运用中,还会考虑时间开销、存储开销、可解释性等方面的因素)
模型评估
使用测试误差近似泛化误差。
- 在没有独立的测试集的前提下,需要对已有的数据集进行划分产生训练集和测试集用于训练和测试算法。所以,划分数据的方法有以下几种。
| 方法 | 原理 | 注意 | 优缺点 |
|---|---|---|---|
| 留出法 | 将数据集划分为两个互斥的集合分别作为训练集和测试集 | 1、要尽可能保持数据分布一致性,否则会引入偏差; 2、一般采用若干次随机划分,重复进行实验评估取平均作为最终的结果; 3、常用2/3~4/5的样本作为训练集,其余为测试集。 | 容易引入额外的偏差; |
| 交叉验证 | 将集合划分成k个相似的互斥子集,每次用一个做为测试集,k-1个作为训练集,k次后取平均或投票 | 结果更加精确,但是计算开销大 | |
| 自助法 | 有放回的随机从n个样本中抽取m次 | 1、在数据集小,难以存放划分时很有用; 2、能产生不同的训练集,对集成方法有很大好处; 3、改变了初始数据集分布,引入估计偏差 |
性能度量
性能度量时衡量泛化能力的评价标准,它反映了任务需求,在对比不同模型的能力时,使用不同模型能力时,使用不同的性能度量往往会导致不同的评价结果。
1、分类
- 错误率与精度:分类错误/正确样本占样本总数的比例。
- 混淆矩阵
真实\预测 正 负 正 TP(真正例) FN(假反例) 负 FP(假正例) TN(真反例) - 准确率:预测为正的所有样中有多少是真正的正样本。
P
r
e
c
i
s
i
o
n
=
T
P
T
P
+
F
P
Precision=\frac{TP}{TP+FP}
Precision=TP+FPTP
召回率:为正的所有样本中有多少被预测为真。 P r e c i s i o n = T P T P + F N Precision=\frac{TP}{TP+FN} Precision=TP+FNTP
准确率和召回率,是一对矛盾的度量,准确率越高,召回率反而越低。当然我们希望两者都高,一般情况下,我们取两者达到平衡的点(P-R曲线)。 - P-R曲线 \ BEP:

如上图,A、B、C三个模型的P-R曲线中,A的平衡点BEP最大,所以,A模型相对B\C更优。 - F1分数:也是一种平衡准确率和召回率的度量。 F 1 = 2 1 P r e c i s i o n + 1 R e c a l l = 2 P r e c i s i o n ∗ R e c a l l P r e c i s i o n + R e c a l l F1=\frac{2}{\frac{1}{Precision}+\frac{1}{Recall}}=\frac{2Precision*Recall}{Precision+Recall} F1=Precision1+Recall12=Precision+Recall2Precision∗Recall
- ROC \ AUC:
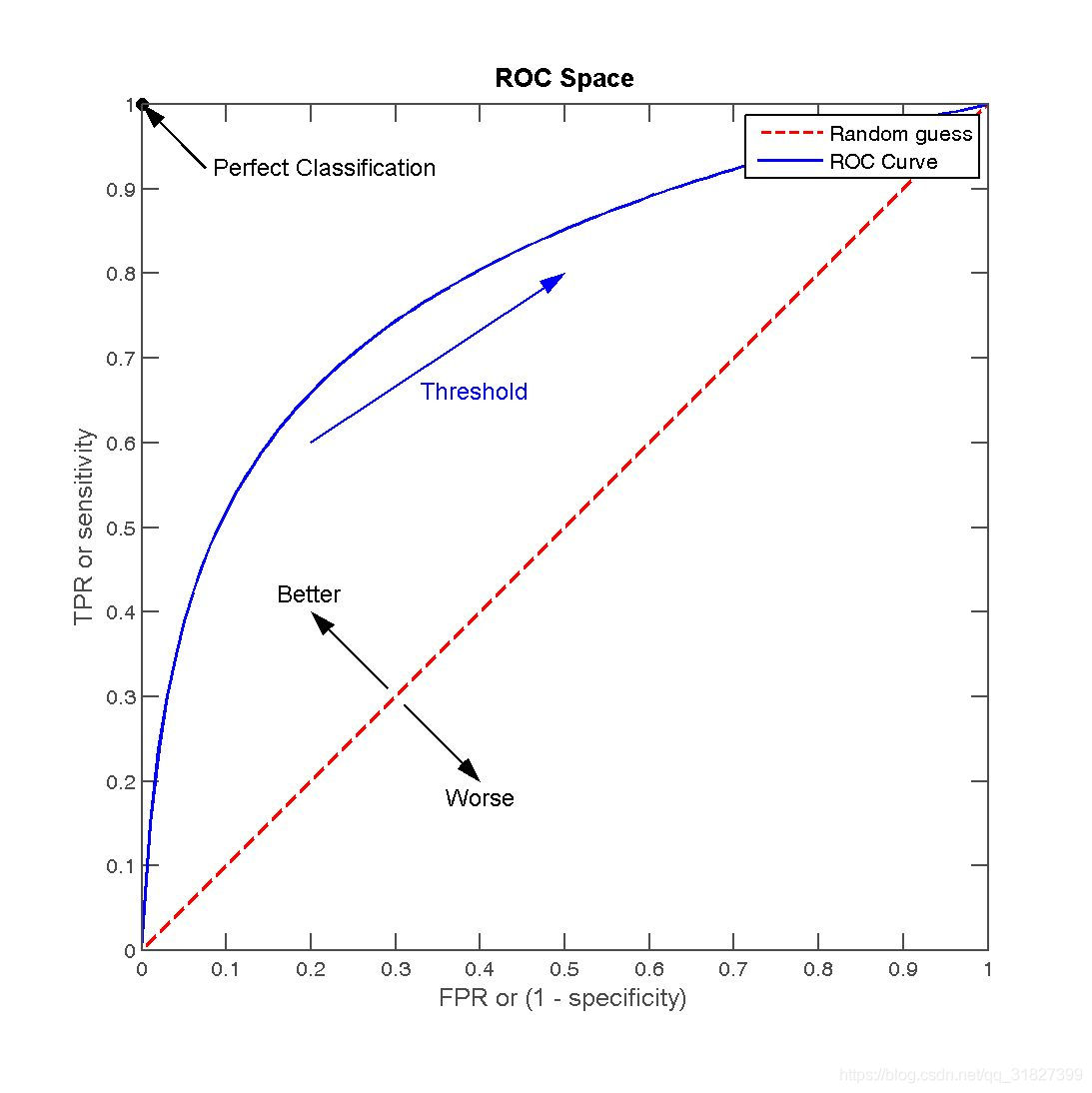
ROC(受试者工作特征曲线)以假正率为横坐标,以真正率为纵坐标,曲线下方的面积(AUC)越大意味着分类效果更好。 - 对数损失 \ 逻辑回归损失 \ 交叉熵损失: L = − [ y log ( y ^ ) + ( 1 − y ) log ( 1 − y ^ ) ] L=-[y\log(\hat y)+(1-y)\log(1-\hat y)] L=−[ylog(y^)+(1−y)log(1−y^)]
- hinge损失(svm): L ( w , y ) = m a x { 0 , 1 − w y } = ∣ 1 − w y ∣ + L(w,y)=max\{0,1-wy\}=|1-wy|_+ L(w,y)=max{0,1−wy}=∣1−wy∣+
2、回归
- MAE: M A E ( y , y ^ ) = 1 m ∑ i m ∣ y i − y ^ i ∣ MAE(y,\hat y)=\frac{1}{m}\sum_i^m|y_i-\hat y_i| MAE(y,y^)=m1∑im∣yi−y^i∣
- MSE: M S E ( y , y ^ ) = 1 m ∑ i m ( y i − y ^ i ) 2 MSE(y,\hat y)=\frac{1}{m}\sum_i^m(y_i-\hat y_i)^2 MSE(y,y^)=m1∑im(yi−y^i)2
- R^2: R 2 ( y , y ^ ) = 1 − ∑ i m ( y i − y ^ i ) ∑ i m ( y i − y ˉ i ) R^2(y,\hat y)=1-\frac{\sum_i^m(y_i-\hat y_i)}{\sum_i^m(y_i-\bar y_i)} R2(y,y^)=1−∑im(yi−yˉi)∑im(yi−y^i)
3、聚类
聚类是将样本划分为若干互不相交的子集(样本簇),当然我们希望是簇内相似度高,簇间相似度低。
此时需要性能度量,一般分两类:
- 外部指标:将聚类结果与某个参考模型作比较。
- 内部指标:直接对聚类结果进行分析,不进行参考。


