有环的单链表快慢指针一定会相遇的证明以及确定环的入口节点方法的证明_快慢指针为什么一定会相遇在入口

我们知道判断一个单链表是否有环最好的方法就是用快慢指针，两个指针都从链表头节点开始，慢指针每次走一个节点，快指针每次走两个节点，如果快慢指针再次相遇的时候，说明链表有环，那你有没有产生一个疑惑，为什么快慢指针一定能够再次相遇，会不会出现快指针每次快追上慢指针的时候都会直接跳过慢指针的情况出现呢，下面就试图从数学原理上来证明为什么快慢指针一定会出现重合的时候

例如上图的一个有环单链表，环的入口在标号为0的位置，环上一共有 k + 1个节点，那环的最后一个节点（指入口节点的上一个节点）标号即为k，假设现在慢指针第一次来到了环的0号位置，那快指针必然已经停在环的某个节点上，假设是环的第 i 个节点位置上 （0 < i <= k），从这时开始快慢指针再跳 x 次来到的位置则分别为
慢指针位置：p1 = x % (k+1)
快指针位置：p2 = (i + 2x) % (k+1) 即 p2 =（i + x + x）%（k+1）
可以看出，只要满足 i + x 正好是 (k+1) 的整数倍，那么就必然存在 p1 = p2

例如当 x + i = k + 1, 即 x = k + 1 - i 时:
p1 = (k + 1 - i) % (k + 1) = k + 1 - i
p2 = (2k + 2 - i) % (k+1) = (k + 1 + k + 1 - i) % (k + 1) = (k + 1 - i) % (k+1) = k + 1 - i = p1

假设现在 i = 3， k = 6， 则 x = 4，即再走4次，则快慢指针都来到了标号为4的节点上

下面继续看另一个问题，当快慢指针相遇时，这时再拿一个慢指针2放在链表头节点的位置，慢指针1保持原位，然后两个慢指针同时移动，当两个慢指针第一次相遇时，相遇的位置为什么一定就是环的入口节点位置

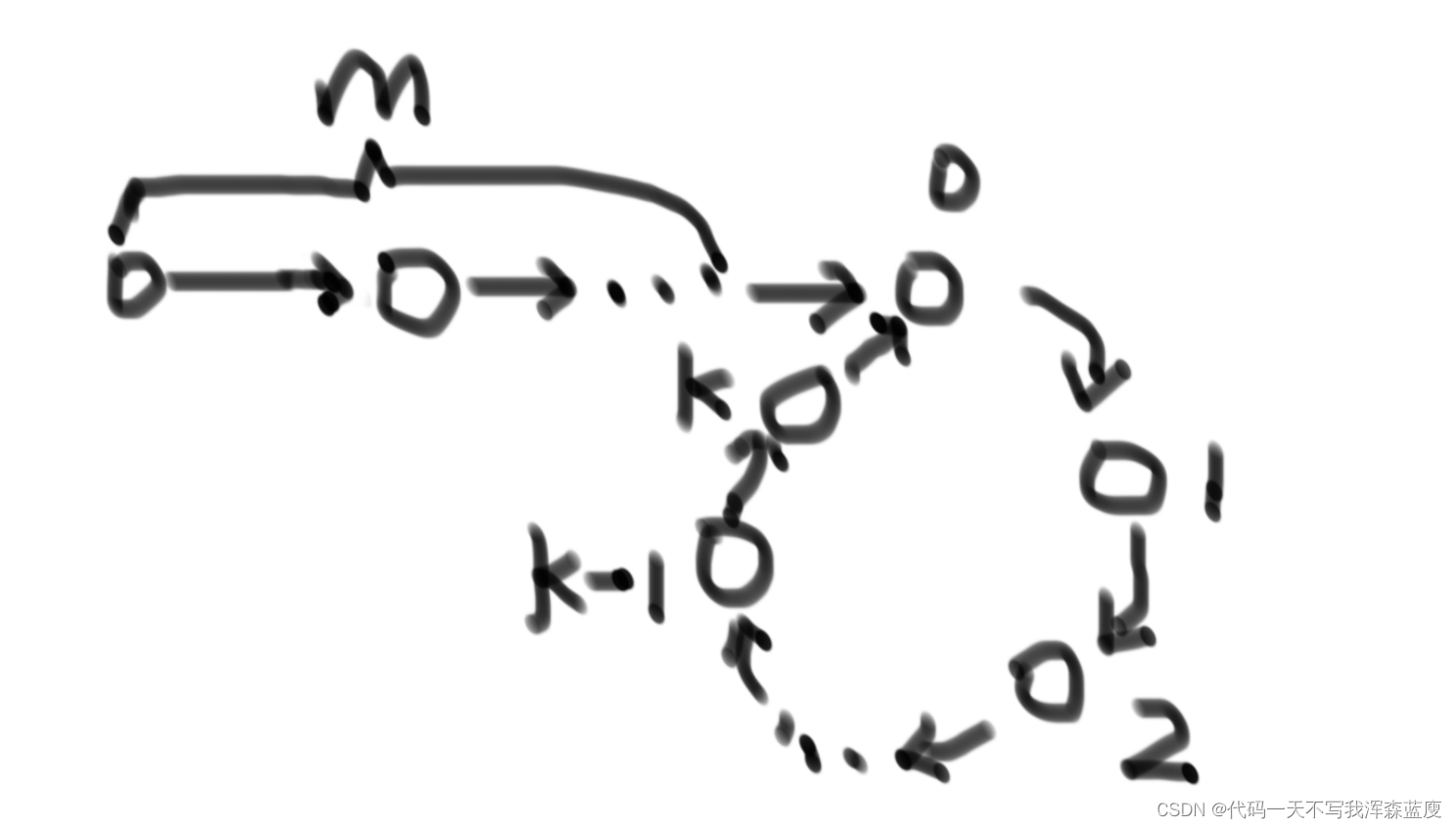
以上图为例，假设从链表头节点到环的入口节点（不包括环的入口节点）一共有m个节点，而环上一共有k+1个节点（包括环的入口节点），则慢指针走 m 次 会到达 m + 1的位置，即环的入口位置上，此时快指针停在 m % (k + 1) 的位置上，根据之前的证明，走一定次数快慢指针一定能够在环上的某处重合，现假设再跳x次它们相遇，则有
x % (k+1) = (2x + m) % (k + 1) = (x + m + x) % (k+1)，则必然有 x + m 为 k + 1 的整数倍，

这时再放一个慢指针2在链表的头节点上，然后两个慢指针同时移动，
慢指针2至少需要跳动m次到达环的入口点，慢指针1跳动m次会到达 (x + m) % (k+1)，由于上面已经推导出 x + m 为 k + 1的整数倍，所以此时慢指针1也正好处于环的入口节点上，所以两个快慢指针第一次相遇必然是在环的入口节点上。

特别的，当 m = 0, 也即链表的头节点就是环的入口节点，x % (k+1) = (2x + m) % (k + 1) 则变为 x % (k+1) = 2x % (k+1)，则必然有 x 为 （k+1）的整数倍，此时快慢指针都在链表的头节点上，这时再放一个慢指针2到链表的头节点，则两个慢指针直接重合，即慢指针2一步也不需要动就和慢指针1重合，仍然符合至少需要移动m次的条件。