【数据结构】图的深度遍历与广度遍历_深度遍历和广度遍历

作者：从前慢现在也慢 | 2024-07-10 04:10:25

踩

深度遍历和广度遍历

图是一种常见的数据格式，它的遍历主要分为两种：

深度优先遍历(DFS):类似于二叉树的前序前序遍历

广度优先遍历(BFS):类似于二叉树的层次遍历

一、出度与入度

在讲图的遍历之前，我们需要先了解图的数据结构。

对于图，我们一般定义横向是出度，纵向是入度。比如对于左图我们转成领接矩阵如右图

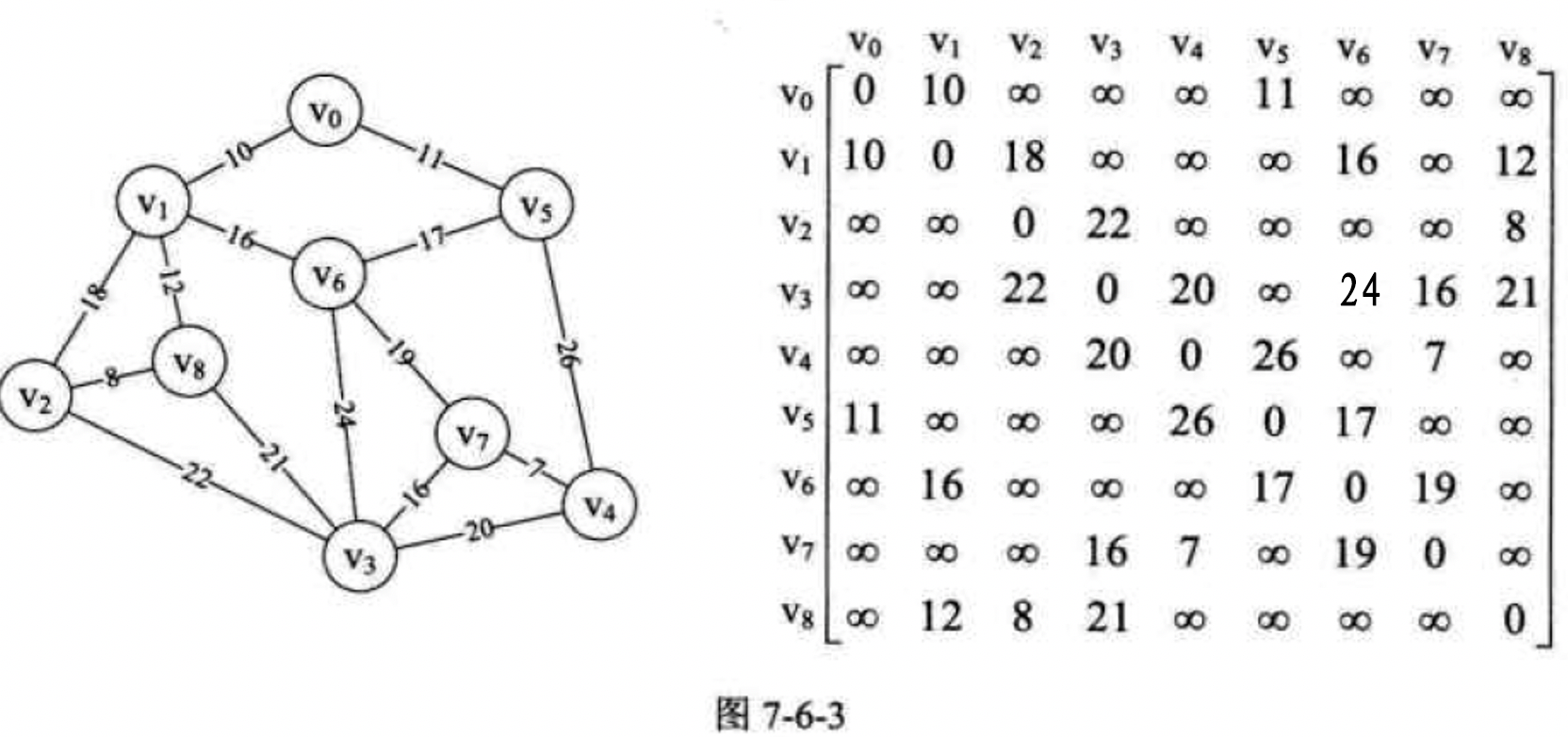
这里我们构建一个图的数据结构Graph，顺序遍历二维数组matrix的index[0]、index[1]、index[2]···获取出度。同理顺序遍历[0]index···获取入度。用java实现如下：

public class Graph {
    private int vertexSize;//顶点数量
    private int[] vertexs;//顶点数组
    private int[][] matrix;//边或者弧的矩阵
    private static final int MAX_WEIGHT = 1000;//无穷大常量
    private boolean[] isVisited;

    public Graph(int vertexSize) {
        this.vertexSize = vertexSize;
        matrix = new int[vertexSize][vertexSize];
        // 初始化顶点数组为123···
        vertexs = new int[vertexSize];
        for (int i = 0; i < vertexSize; i++) {
            vertexs[i] = i;
        }
        isVisited = new boolean[vertexSize];
    }

    // 获取某个顶点的出度
    public int getOutDegree(int index) {
        int degree = 0;
        for (int j = 0; j < matrix[index].length; j++) {
            int weight = matrix[index][j];
            if (weight != 0 && weight != MAX_WEIGHT) {
                degree++;
            }
        }
        return degree;
    }

    // 获取某个顶点的入度
    public int getInDegree(int index) {
        int degree = 0;
        for (int j = 0; j < matrix.length; j++) {
            int weight = matrix[j][index];
            if (weight != 0 && weight != MAX_WEIGHT) {
                degree++;
            }
        }
        return degree;
    }
    public static void main(String[] args) {
        Graph graph = new Graph(9);

        int[] a1 = new int[]{0, 10, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT};
        int[] a2 = new int[]{10, 0, 18, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, MAX_WEIGHT, 12};
        int[] a3 = new int[]{MAX_WEIGHT, MAX_WEIGHT, 0, 22, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 8};
        int[] a4 = new int[]{MAX_WEIGHT, MAX_WEIGHT, 22, 0, 20, MAX_WEIGHT, 24, 16, 21};
        int[] a5 = new int[]{MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 20, 0, 26, MAX_WEIGHT, 7, MAX_WEIGHT};
        int[] a6 = new int[]{11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 26, 0, 17, MAX_WEIGHT, MAX_WEIGHT};
        int[] a7 = new int[]{MAX_WEIGHT, 16, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 17, 0, 19, MAX_WEIGHT};
        int[] a8 = new int[]{MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, 7, MAX_WEIGHT, 19, 0, MAX_WEIGHT};
        int[] a9 = new int[]{MAX_WEIGHT, 12, 8, 21, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0};

        graph.matrix[0] = a1;
        graph.matrix[1] = a2;
        graph.matrix[2] = a3;
        graph.matrix[3] = a4;
        graph.matrix[4] = a5;
        graph.matrix[5] = a6;
        graph.matrix[6] = a7;
        graph.matrix[7] = a8;
        graph.matrix[8] = a9;

        System.out.println("v4的出度:" + graph.getOutDegree(4));
        System.out.println("v4的入度:" + graph.getInDegree(4));
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

经验证输出

v4的出度:3
v4的入度:3

二、深度优先遍历

深度优先遍历(Deep_First_Search,简称为DFS):它从图中某个顶点ⅴ出发，访问此顶点，然后从v的未被访问的邻接点出发深度优先遍历图，直至图中所有和 v 有路径相通的顶点都被访问到。

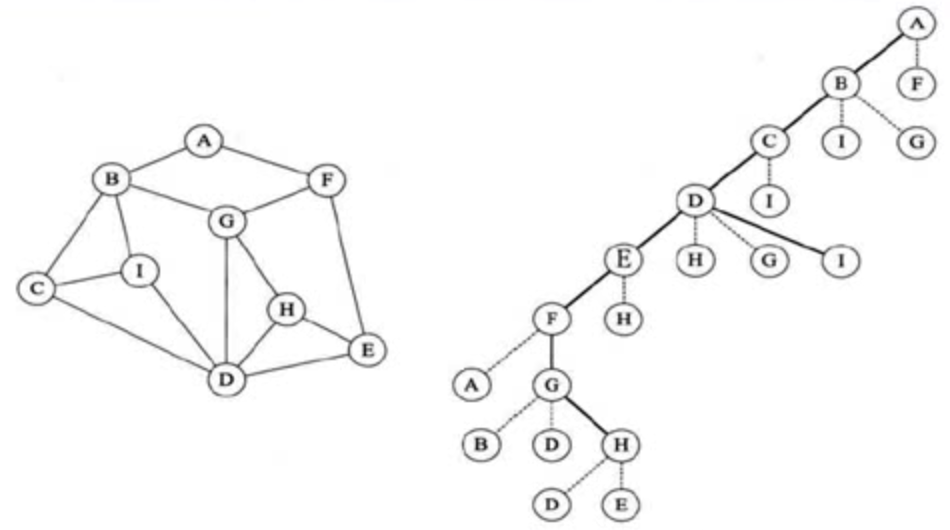
如上图所示，按照上图所示，深度遍历顺序应该是ABCDEFGHI。

遍历过程：A->B B->C C->D D->E E->F F->G G->H,然后回到B,B->I。类似于二叉树的前序前序遍历方式(DLR)，中 -> 左 -> 右。

已知原理，下面用java实现。首先对数组的每一层进行depthFirstSearch(index)遍历，其中isVisited用于记录该顶点是否遍历过

/**
 * 对外公开的深度优先遍历
 */
public void depthFirstSearch() {
    isVisited = new boolean[vertexSize];
    for (int i = 0; i < vertexSize; i++) {
        if (!isVisited[i]) {
            System.out.println("访问到了：" + i + "顶点");
            depthFirstSearch(i);
        }
    }
    isVisited = new boolean[vertexSize];
}
1
2
3
4
5
6
7
8
9
10
11
12
13

对于depthFirstSearch(index)的具体实现：首先获取某个顶点的第一个邻接点(getFirstNeighbor)，然后对于该顶点递归循环获取第一个临界点以达到深度的效果。如果遍历不到则获取相对于改顶点的下一个邻接点，同样用isVisited字段标记是否访问过。

/**
 * 图的深度优先遍历算法
 */
private void depthFirstSearch(int i) {
    isVisited[i] = true;
    int w = getFirstNeighbor(i);//
    while (w != -1) {
        if (!isVisited[w]) {
            //需要遍历该顶点
            System.out.println("访问到了：" + w + "顶点");
            depthFirstSearch(w);
        }
        w = getNextNeighbor(i, w);//第一个相对于w的邻接点
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

对于这两个辅助函数的实现如下

其中getFirstNeighbor肯定会从0查找它的出度(这里我们用不上入度)，因为要确保不会遗漏。而对于getNextNeighbor我们则需要从index+1查找它的出度，因为深度优先的话，序列号在前面的顶点已被遍历过了不需要重复损耗性能。

/**
 * 获取某个顶点的第一个邻接点
 */
public int getFirstNeighbor(int index) {
    for (int j = 0; j < vertexSize; j++) {
        if (matrix[index][j] > 0 && matrix[index][j] < MAX_WEIGHT) {
            return j;
        }
    }
    return -1;
}

/**
 * 根据前一个邻接点的下标来取得下一个邻接点
 *
 * @param v 表示要找的顶点
 * @param index 表示该顶点相对于哪个邻接点去获取下一个邻接点
 */
public int getNextNeighbor(int v, int index) {
    for (int j = index + 1; j < vertexSize; j++) {
        if (matrix[v][j] > 0 && matrix[v][j] < MAX_WEIGHT) {
            return j;
        }
    }
    return -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

最后调用graph.depthFirstSearch();函数验证如下

访问到了：0顶点
访问到了：1顶点
访问到了：2顶点
访问到了：3顶点
访问到了：4顶点
访问到了：5顶点
访问到了：6顶点
访问到了：7顶点
访问到了：8顶点

三、广度优先遍历

广度优先遍历(Broad_First_Search,简称为BFS):它从图中某个顶点ⅴ出发，访问此顶点，然后从v的未被访问的邻接点出发广度优先遍历图，直至图中所有和 v 有路径相通的顶点都被访问到。

还是这个图，广度遍历顺序应该是0 1 5 2 6 8 4 3 7。

遍历过程：第一层0 0->1 0->5 第二层1->2 1->6 1->8 5->4 第三层2->3 第四层3->7。类似于二叉树的层次遍历。

已知原理，下面用java实现。首先对数组的每一层进行broadFirstSearch(index)遍历，其中isVisited用于记录该顶点是否遍历过

public void broadFirstSearch() {
    isVisited = new boolean[vertexSize];
    for (int i = 0; i < vertexSize; i++) {
        if (!isVisited[i]) {
            broadFirstSearch(i);
        }
    }
}
1
2
3
4
5
6
7
8

对于broadFirstSearch(index)，我们需要用到队列，每次广度优先遍历都会入队列，然后遍历它所有的邻接点，完了之后退一个队列，继续广度遍历，当然遍历完成的标志就是队列清空。

比如这里我们入队v0,然后再第一层while循环中退队v0，同时找到w为v1，然后在第二层while循环中继续遍历v0的所有邻接点得到v5入栈。然后返回到第一层while循环对v1进行广度遍历。

/**
 * 实现广度优先遍历
 *
 * @param i
 */
private void broadFirstSearch(int i) {
    int u, w;
    LinkedList<Integer> queue = new LinkedList<Integer>();
    System.out.println("访问到：" + i + "顶点");
    isVisited[i] = true;
    queue.add(i);//第一次把v0加到队列
    while (!queue.isEmpty()) {
        u = (queue.removeFirst()).intValue();
        w = getFirstNeighbor(u);
        while (w != -1) {
            if (!isVisited[w]) {
                System.out.println("访问到了：" + w + "顶点");
                isVisited[w] = true;
                queue.add(w);
            }
            w = getNextNeighbor(u, w);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

运行graph.broadFirstSearch();获取结果

访问到：0顶点
访问到了：1顶点
访问到了：5顶点
访问到了：2顶点
访问到了：6顶点
访问到了：8顶点
访问到了：4顶点
访问到了：3顶点
访问到了：7顶点

四、demo源码

import java.util.LinkedList;

public class Graph {
    private int vertexSize;//顶点数量
    private int[] vertexs;//顶点数组
    private int[][] matrix;//边或者弧的矩阵
    private static final int MAX_WEIGHT = 1000;//无穷大常量
    private boolean[] isVisited;

    public Graph(int vertexSize) {
        this.vertexSize = vertexSize;
        matrix = new int[vertexSize][vertexSize];
        // 初始化顶点数组为123···
        vertexs = new int[vertexSize];
        for (int i = 0; i < vertexSize; i++) {
            vertexs[i] = i;
        }
        isVisited = new boolean[vertexSize];
    }

    // 获取某个顶点的出度
    public int getOutDegree(int index) {
        int degree = 0;
        for (int j = 0; j < matrix[index].length; j++) {
            int weight = matrix[index][j];
            if (weight != 0 && weight != MAX_WEIGHT) {
                degree++;
            }
        }
        return degree;
    }

    // 获取某个顶点的入度
    public int getInDegree(int index) {
        int degree = 0;
        for (int j = 0; j < matrix.length; j++) {
            int weight = matrix[j][index];
            if (weight != 0 && weight != MAX_WEIGHT) {
                degree++;
            }
        }
        return degree;
    }

    // 获取两个顶点之间的权值
    public int getWeight(int v1, int v2) {
        int weight = matrix[v1][v2];
        return weight == 0 ? 0 : (weight == MAX_WEIGHT ? -1 : weight);
    }

    /**
     * 对外公开的深度优先遍历
     */
    public void depthFirstSearch() {
        isVisited = new boolean[vertexSize];
        for (int i = 0; i < vertexSize; i++) {
            if (!isVisited[i]) {
                System.out.println("访问到了：" + i + "顶点");
                depthFirstSearch(i);
            }
        }
        isVisited = new boolean[vertexSize];
    }

    /**
     * 图的深度优先遍历算法
     */
    private void depthFirstSearch(int i) {
        isVisited[i] = true;
        int w = getFirstNeighbor(i);//
        while (w != -1) {
            if (!isVisited[w]) {
                //需要遍历该顶点
                System.out.println("访问到了：" + w + "顶点");
                depthFirstSearch(w);
            }
            w = getNextNeighbor(i, w);//第一个相对于w的邻接点
        }
    }

    /**
     * 获取某个顶点的第一个邻接点
     */
    public int getFirstNeighbor(int index) {
        for (int j = 0; j < vertexSize; j++) {
            if (matrix[index][j] > 0 && matrix[index][j] < MAX_WEIGHT) {
                return j;
            }
        }
        return -1;
    }

    /**
     * 根据前一个邻接点的下标来取得下一个邻接点
     *
     * @param v 表示要找的顶点
     * @param index 表示该顶点相对于哪个邻接点去获取下一个邻接点
     */
    public int getNextNeighbor(int v, int index) {
        for (int j = index + 1; j < vertexSize; j++) {
            if (matrix[v][j] > 0 && matrix[v][j] < MAX_WEIGHT) {
                return j;
            }
        }
        return -1;
    }

    public void broadFirstSearch() {
        isVisited = new boolean[vertexSize];
        for (int i = 0; i < vertexSize; i++) {
            if (!isVisited[i]) {
                broadFirstSearch(i);
            }
        }
    }

    /**
     * 实现广度优先遍历
     *
     * @param i
     */
    private void broadFirstSearch(int i) {
        int u, w;
        LinkedList<Integer> queue = new LinkedList<Integer>();
        System.out.println("访问到：" + i + "顶点");
        isVisited[i] = true;
        queue.add(i);//第一次把v0加到队列
        while (!queue.isEmpty()) {
            u = (queue.removeFirst()).intValue();
            w = getFirstNeighbor(u);
            while (w != -1) {
                if (!isVisited[w]) {
                    System.out.println("访问到了：" + w + "顶点");
                    isVisited[w] = true;
                    queue.add(w);
                }
                w = getNextNeighbor(u, w);
            }
        }
    }

    public static void main(String[] args) {
        Graph graph = new Graph(9);

        int[] a1 = new int[]{0, 10, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT};
        int[] a2 = new int[]{10, 0, 18, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, MAX_WEIGHT, 12};
        int[] a3 = new int[]{MAX_WEIGHT, MAX_WEIGHT, 0, 22, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 8};
        int[] a4 = new int[]{MAX_WEIGHT, MAX_WEIGHT, 22, 0, 20, MAX_WEIGHT, 24, 16, 21};
        int[] a5 = new int[]{MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 20, 0, 26, MAX_WEIGHT, 7, MAX_WEIGHT};
        int[] a6 = new int[]{11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 26, 0, 17, MAX_WEIGHT, MAX_WEIGHT};
        int[] a7 = new int[]{MAX_WEIGHT, 16, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 17, 0, 19, MAX_WEIGHT};
        int[] a8 = new int[]{MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, 7, MAX_WEIGHT, 19, 0, MAX_WEIGHT};
        int[] a9 = new int[]{MAX_WEIGHT, 12, 8, 21, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0};

        graph.matrix[0] = a1;
        graph.matrix[1] = a2;
        graph.matrix[2] = a3;
        graph.matrix[3] = a4;
        graph.matrix[4] = a5;
        graph.matrix[5] = a6;
        graph.matrix[6] = a7;
        graph.matrix[7] = a8;
        graph.matrix[8] = a9;

        System.out.println("v4的出度:" + graph.getOutDegree(4));
        System.out.println("v4的入度:" + graph.getInDegree(4));
        System.out.println("<v2,v3>的权值：" + graph.getWeight(2, 3));
//        graph.depthFirstSearch();
        graph.broadFirstSearch();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171

声明：本文内容由网友自发贡献，转载请注明出处：【wpsshop博客】