14届蓝桥杯 pythonB组 保险箱_蓝桥杯python大学b组14

小蓝有一个保险箱，保险箱上共有 n 位数字。

小蓝可以任意调整保险箱上的每个数字，每一次操作可以将其中一位增加 1 或减少 1。

当某位原本为 9 或 0 时可能会向前（左边）进位/退位，当最高位（左边第一位）上的数字变化时向前的进位或退位忽略。

例如:

00000 的第 5 位减 1 变为 99999；

99999 的第 5 位减 1 变为 99998；

00000的第 4 位减 1 变为 99990；

97993 的第 4 位加 1 变为 98003；

99909 的第 3 位加 1 变为 00009。

保险箱上一开始有一个数字 x，小蓝希望把它变成 y，这样才能打开它，问小蓝最少需要操作的次数。

输入格式
输入的第一行包含一个整数 n。

第二行包含一个 n 位整数 x。

第三行包含一个 n 位整数 y。

输出格式
输出一行包含一个整数表示答案。

数据范围
对于 30% 的评测用例，1≤n≤300；
对于 60% 的评测用例，1≤n≤3000；
对于所有评测用例，1≤n≤10^5，x,y中仅包含数字 0 至 9，可能有前导零
————————————————

由题意，左侧变化不带动右侧变化，而右侧变化可能导致左端变化（进位，退位），所以我们应该从右端往左端操作

每个位置的操作分为三种

• 1.通过减法而退位到达目标 （如2通过 -2 到0 再 -2 到8）
• 2.通过加法而进位到达目标 （如 8通过 +2 到0 再 +2 到 2）
• 3.通过加/减法 不进不退位到达目标 （如2 通过+ 6 直接到8；8 直接 -6 到2）

下面简称为 “减退”， “加进”， “不进退”

每种方式对应的操作次数为：

• 减退： 10 - 目标 + 自身

• 加进： 10 - 自身 + 目标

• 不进退： | 目标 - 自身 |

• 而递推公式中的自身 会由于右端的操作而改变

• 如右端加进 左端数 要 + 1，右端 减退 左端数 要 -1

• 下面用图解方式讲述思路

• 每个位置有三种操作：根据对应的公式计算
  
• 左端的数也对应3种操作，每个操作种的自身这个变量要根据右端执行的操作而改变。下面以左端减退为例，根据右端执行的操作改变自身
  
• 除了减退，加进和不进退也要根据右端的操作进行改变
  

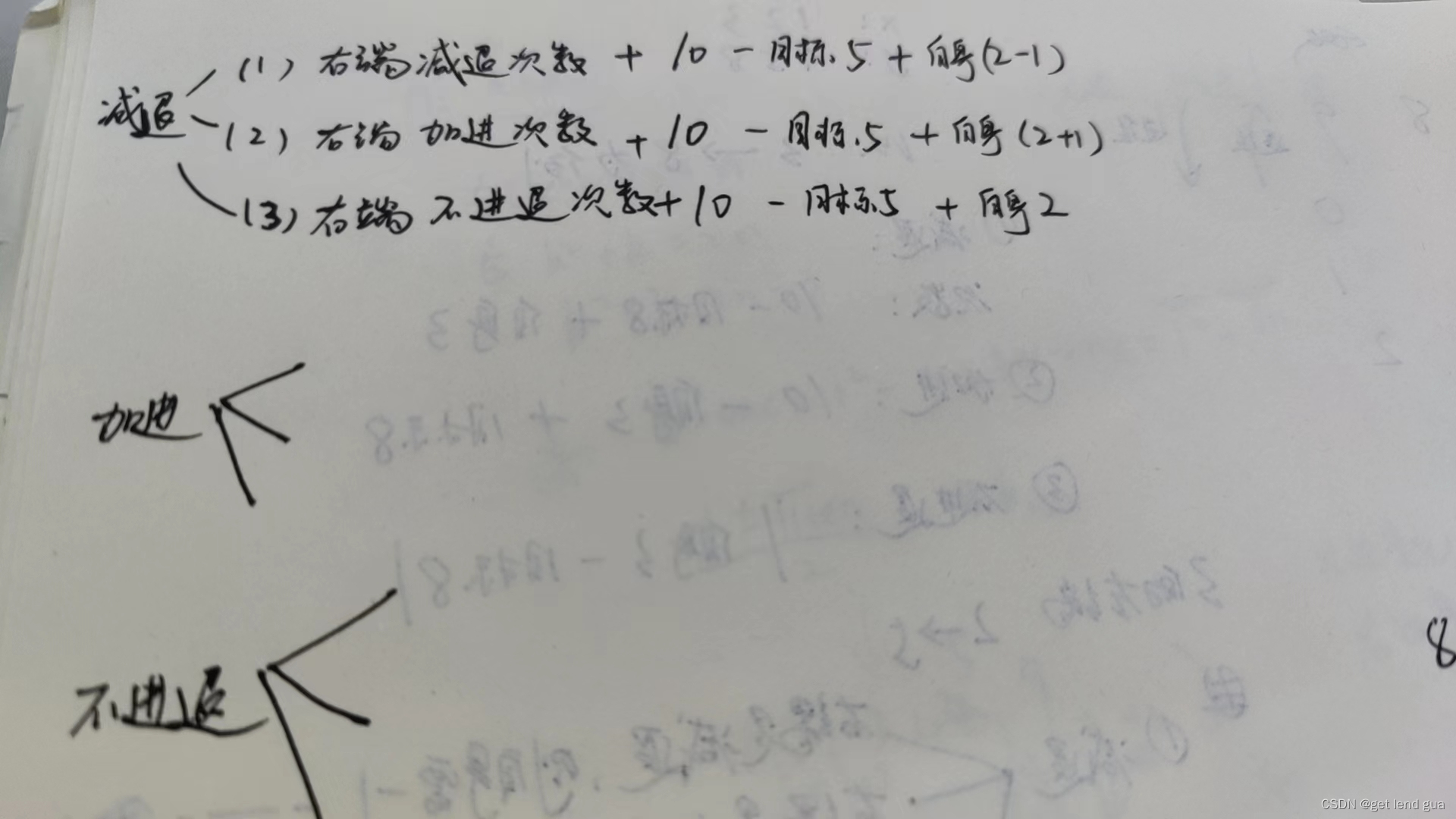
每种操作中对应三种情况 选取最小的。

当遍历到最左端时，选取三种累积操作数中最小者即是所求。

# 保险箱
# 从末端开始操作
# 每个位置的操作分为三种
# 1. 通过减法而退位到达目标 2.通过加法而进位到达目标 3.通过加/减法 不进不退位到达目标
# 下面简称为 “减退”， “加进”， “不进退”

n = int(input())
x = list(map(int,str(input()))) # 自身
y = list(map(int,str(input()))) # 目标
dp = [[0,0,0] for _ in range(n)]
dp[-1] = [10- y[-1] + x[-1], 10 - x[-1] + y[-1],abs(x[-1] - y[-1]) ]
for i in range(n-2,-1,-1):
    # 1. 本次通过减法而退位到达目标
    # 1.1 右端是通过减退到达目标的
    r_sub = dp[i+1][0] + 10 - y[i] + (x[i] - 1)
    # 1.2 右端是通过加进达到目标的
    r_add = dp[i+1][1] + 10 - y[i] + (x[i] + 1)
    # 1.3 右端是不进退到达目标的
    r_not = dp[i+1][2] + 10 - y[i] + x[i]
    dp[i][0] = min(r_sub,r_add,r_not)

    # 2. 本次是通过加法而进位到达目标
    r_sub = dp[i+1][0] + 10 - (x[i] - 1) + y[i]
    r_add = dp[i+1][1] + 10 - (x[i] + 1) + y[i]
    r_not = dp[i+1][2] + 10 - x[i] + y[i]
    dp[i][1] = min(r_sub,r_add,r_not)

    # 3. 本次是不进位也不退位达到目标
    r_sub = dp[i+1][0] + abs((x[i] - 1) - y[i])
    r_add = dp[i+1][1] + abs((x[i] + 1) - y[i])
    r_not = dp[i+1][2] + abs(x[i] - y[i])
    dp[i][2] = min(r_sub,r_add,r_not)
print(min(dp[0]))



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36